Article contents
Sidewall effects in Rayleigh–Bénard convection
Published online by Cambridge University Press: 17 February 2014
Abstract
We investigate the influence of the temperature boundary conditions at the sidewall on the heat transport in Rayleigh–Bénard (RB) convection using direct numerical simulations. For relatively low Rayleigh numbers 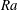 $Ra$ the heat transport is higher when the sidewall is isothermal, kept at a temperature
$Ra$ the heat transport is higher when the sidewall is isothermal, kept at a temperature 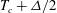 $T_c+\Delta /2$ (where
$T_c+\Delta /2$ (where 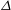 $\Delta $ is the temperature difference between the horizontal plates and
$\Delta $ is the temperature difference between the horizontal plates and 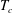 $T_c$ the temperature of the cold plate), than when the sidewall is adiabatic. The reason is that in the former case part of the heat current avoids the thermal resistance of the fluid layer by escaping through the sidewall that acts as a short-circuit. For higher
$T_c$ the temperature of the cold plate), than when the sidewall is adiabatic. The reason is that in the former case part of the heat current avoids the thermal resistance of the fluid layer by escaping through the sidewall that acts as a short-circuit. For higher 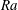 $Ra$ the bulk becomes more isothermal and this reduces the heat current through the sidewall. Therefore the heat flux in a cell with an isothermal sidewall converges to the value obtained with an adiabatic sidewall for high enough
$Ra$ the bulk becomes more isothermal and this reduces the heat current through the sidewall. Therefore the heat flux in a cell with an isothermal sidewall converges to the value obtained with an adiabatic sidewall for high enough  $Ra$ (
$Ra$ (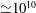 ${\simeq }10^{10}$). However, when the sidewall temperature deviates from
${\simeq }10^{10}$). However, when the sidewall temperature deviates from 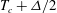 $T_c+\Delta /2$ the heat transport at the bottom and top plates is different from the value obtained using an adiabatic sidewall. In this case the difference does not decrease with increasing
$T_c+\Delta /2$ the heat transport at the bottom and top plates is different from the value obtained using an adiabatic sidewall. In this case the difference does not decrease with increasing 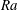 $Ra$ thus indicating that the ambient temperature of the experimental apparatus can influence the heat transfer. A similar behaviour is observed when only a very small sidewall region close to the horizontal plates is kept isothermal, while the rest of the sidewall is adiabatic. The reason is that in the region closest to the horizontal plates the temperature difference between the fluid and the sidewall is highest. This suggests that one should be careful with the placement of thermal shields outside the fluid sample to minimize spurious heat currents. When the physical sidewall properties (thickness, thermal conductivity and heat capacity) are considered the problem becomes one of conjugate heat transfer and different behaviours are possible depending on the sidewall properties and the temperature boundary condition on the ‘dry’ side. The problem becomes even more complicated when the sidewall is shielded with additional insulation or temperature-controlled surfaces; some particular examples are illustrated and discussed. It has been observed that the sidewall temperature dynamics not only affects the heat transfer but can also trigger a different mean flow state or change the temperature fluctuations in the flow and this could explain some of the observed differences between similar but not fully identical experiments.
$Ra$ thus indicating that the ambient temperature of the experimental apparatus can influence the heat transfer. A similar behaviour is observed when only a very small sidewall region close to the horizontal plates is kept isothermal, while the rest of the sidewall is adiabatic. The reason is that in the region closest to the horizontal plates the temperature difference between the fluid and the sidewall is highest. This suggests that one should be careful with the placement of thermal shields outside the fluid sample to minimize spurious heat currents. When the physical sidewall properties (thickness, thermal conductivity and heat capacity) are considered the problem becomes one of conjugate heat transfer and different behaviours are possible depending on the sidewall properties and the temperature boundary condition on the ‘dry’ side. The problem becomes even more complicated when the sidewall is shielded with additional insulation or temperature-controlled surfaces; some particular examples are illustrated and discussed. It has been observed that the sidewall temperature dynamics not only affects the heat transfer but can also trigger a different mean flow state or change the temperature fluctuations in the flow and this could explain some of the observed differences between similar but not fully identical experiments.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 27
- Cited by


