Published online by Cambridge University Press: 14 May 2013
Motivated by the importance of diapycnal mixing parameterizations in large-scale ocean general circulation models, we provide a detailed analysis of high-Reynolds-number mixing in density stratified shear flows which constitute an archetypical example of the small-scale physical processes occurring in the oceanic interior that control turbulent diffusion. Our focus is upon the issue as to whether the route to fully developed turbulence in the stratified mixing layer is in any significant way determinant of diapycnal mixing efficiency as represented by an effective turbulent diffusivity. We characterize different routes to fully developed turbulence by the nature of the secondary instabilities through which a primary Kelvin–Helmholtz billow executes the transition to this state. We then demonstrate that different mechanisms of turbulence transition characterized in these different transition mechanisms lead to considerably different values for the efficiency of diapycnal mixing and also for the effective vertical flux of buoyancy. We show that the widely employed value of 0.15–0.2 for the efficiency of mixing in shear-induced stratified turbulence based upon both laboratory measurements and similarly low-Reynolds-number numerical simulations may be too low for the high-Reynolds-number regime characteristic of geophysical flows. Our results show that the mixing efficiency tends to a value of approximately 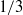 $1/ 3$ for sufficiently large Reynolds number at an intermediate value of 0.12 for the Richardson number. This is in agreement with a theoretical predictions of Caulfield, Tang and Plasting (J. Fluid Mech., vol. 498, 2004, pp. 315–332) for the asymptotic value of mixing efficiency in stratified Couette flows. In the high-Reynolds-number regime, mixing efficiency is shown to vary over a considerable range during the course of a particular shear-induced mixing event. We explain this variation on the basis of a detailed examination of the underlying dynamics. Since values in the range 0.15–0.2 for mixing efficiency have been extensively employed to infer an effective diffusivity from ocean microstructure measurements and also in energy balance analyses of the requirements of the global ocean circulation, our findings have potentially important implications for large-scale ocean modelling. We also quantify the errors introduced by employing the Osborn (J. Phys. Oceanogr., vol. 10, 1980, pp. 83–89) formula along with an efficiency of 0.15 to infer values for effective diffusivity, and explain the logical underpinnings of this conclusion. One of the more important aspects of this work from the perspective of our theoretical understanding of stratified turbulence is the demonstration that the inverse cascade of energy, which is facilitated by the vortex-merging process that is typical of laboratory experiments and of the low-Reynolds-number simulations of shear flow evolution, is strongly suppressed by increase of the Reynolds number to values typical of geophysical flows. Based on this finding, the application of results based on low-Reynolds-number (numerical or laboratory) experiments to high-Reynolds-number geophysical shear flows needs to be reconsidered.
$1/ 3$ for sufficiently large Reynolds number at an intermediate value of 0.12 for the Richardson number. This is in agreement with a theoretical predictions of Caulfield, Tang and Plasting (J. Fluid Mech., vol. 498, 2004, pp. 315–332) for the asymptotic value of mixing efficiency in stratified Couette flows. In the high-Reynolds-number regime, mixing efficiency is shown to vary over a considerable range during the course of a particular shear-induced mixing event. We explain this variation on the basis of a detailed examination of the underlying dynamics. Since values in the range 0.15–0.2 for mixing efficiency have been extensively employed to infer an effective diffusivity from ocean microstructure measurements and also in energy balance analyses of the requirements of the global ocean circulation, our findings have potentially important implications for large-scale ocean modelling. We also quantify the errors introduced by employing the Osborn (J. Phys. Oceanogr., vol. 10, 1980, pp. 83–89) formula along with an efficiency of 0.15 to infer values for effective diffusivity, and explain the logical underpinnings of this conclusion. One of the more important aspects of this work from the perspective of our theoretical understanding of stratified turbulence is the demonstration that the inverse cascade of energy, which is facilitated by the vortex-merging process that is typical of laboratory experiments and of the low-Reynolds-number simulations of shear flow evolution, is strongly suppressed by increase of the Reynolds number to values typical of geophysical flows. Based on this finding, the application of results based on low-Reynolds-number (numerical or laboratory) experiments to high-Reynolds-number geophysical shear flows needs to be reconsidered.