Published online by Cambridge University Press: 03 April 2019
The shear-induced collective diffusivity down a concentration gradient in a viscous emulsion is computed using direct numerical simulation. A layer of randomly packed drops subjected to a shear flow, shows the layer width to increase with the 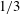 $1/3$ power of time, consistent with a semi-dilute theory that assumes a diffusivity linear with concentration. This characteristic scaling and the underlying theory are used to compute the collective diffusivity coefficient. This is the first ever computation of this quantity for a system of deformable particles using fully resolved numerical simulation. The results match very well with previous experimental observations. The coefficient of collective diffusivity varies non-monotonically with the capillary number, due to the competing effects of increasing deformation and drop orientation. A phenomenological correlation for the collective diffusivity coefficient as a function of capillary number is presented. We also apply an alternative approach to compute collective diffusivity, developed originally for a statistically homogeneous rigid sphere suspension – computing the dynamic structure factor from the simulated droplet positions and examining its time variation at small wavenumber. We show that the results from this alternative approach qualitatively agree with our computation of collective diffusivity including the prediction of the non-monotonic variation of diffusivity with the capillary number.
$1/3$ power of time, consistent with a semi-dilute theory that assumes a diffusivity linear with concentration. This characteristic scaling and the underlying theory are used to compute the collective diffusivity coefficient. This is the first ever computation of this quantity for a system of deformable particles using fully resolved numerical simulation. The results match very well with previous experimental observations. The coefficient of collective diffusivity varies non-monotonically with the capillary number, due to the competing effects of increasing deformation and drop orientation. A phenomenological correlation for the collective diffusivity coefficient as a function of capillary number is presented. We also apply an alternative approach to compute collective diffusivity, developed originally for a statistically homogeneous rigid sphere suspension – computing the dynamic structure factor from the simulated droplet positions and examining its time variation at small wavenumber. We show that the results from this alternative approach qualitatively agree with our computation of collective diffusivity including the prediction of the non-monotonic variation of diffusivity with the capillary number.