Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T20:17:53.877Z Has data issue: false hasContentIssue false
  • English
  • Français

Sheared free-surface flow over three-dimensional obstructions of finite amplitude

Published online by Cambridge University Press:  18 September 2019

Andreas H. Akselsen Open the ORCID record for Andreas H. Akselsen [Opens in a new window]  and
Simen Å. Ellingsen Open the ORCID record for Simen Å. Ellingsen [Opens in a new window]
Andreas H. Akselsen*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
Simen Å. Ellingsen
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When shallow water flows over uneven bathymetry, the water surface is modulated. This type of problem has been revisited numerous times since it was first studied by Lord Kelvin in 1886. Our study analytically examines currents whose unperturbed velocity profile 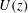$U(z)$ follows a power law 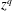$z^{q}$, flowing over a three-dimensional uneven bed. This particular form of 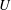$U$, which can model a miscellany of realistic flows, allows explicit analytical solutions. Arbitrary bed shapes can readily be imposed via Fourier’s theorem provided their steepness is moderate. Three-dimensional vorticity–bathymetry interaction effects are evident when the flow makes an oblique angle with a sinusoidally corrugated bed. Streamlines are found to twist and the fluid particle drift is redirected away from the direction of the unperturbed current. Furthermore, a perturbation technique is developed which satisfies the bottom boundary condition to arbitrary order also for large-amplitude obstructions which penetrate well into the current profile. This introduces higher-order harmonics of the bathymetry amplitude. States of resonance for first- and higher-order harmonics are readily calculated. Although the method is theoretically restricted to bathymetries of moderate inclination, a wide variety of steeper obstructions are satisfactorily represented by the method, even provoking occurrences of recirculation. All expressions are analytically explicit and sequential fast Fourier transformations ensure quick and easy computation for arbitrary three-dimensional bathymetries. A method for separating near and far fields ensures computational convergence under the appropriate radiation condition.

JFM classification

Geophysical and Geological Flows: River dynamics Geophysical and Geological Flows: Shallow water flows Waves/Free-surface Flows: Shear waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 740 - 767
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdullah, A. J. 1949 Wave motion at the surface of a current which has an exponential distribution of vorticity. Ann. N.Y. Acad. Sci. 51, 425–441.Google Scholar
Akselsen, A. H. & Ellingsen, S. Å. 2019 Weakly nonlinear transient waves on a shear current: ring waves and skewed Langmuir rolls. J. Fluid Mech. 863, 114–149.Google Scholar
Akylas, T. R. 1984 On the excitation of long nonlinear water waves by a moving pressure distribution. J. Fluid Mech. 141, 455–466.Google Scholar
Barenblatt, G. I. 1993 Scaling laws for fully developed turbulent shear flows. Part 1. Basic hypotheses and analysis. J. Fluid Mech. 248, 513–520.Google Scholar
Bender, C. M. & Orszag, S. A. 1991 Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer.Google Scholar
Benjamin, T. B. 1959 Shearing flow over a wavy boundary. J. Fluid Mech. 6, 161–205.Google Scholar
Benney, D. J. 1961 A non-linear theory for oscillations in a parallel flow. J. Fluid Mech. 10, 209–236.Google Scholar
Bergstrom, D. J., Tachie, M. F. & Balachandar, R. 2001 Application of power laws to low Reynolds number boundary layers on smooth and rough surfaces. Phys. Fluids 13, 3277–3284.Google Scholar
Binder, B. J., Blyth, M. G. & McCue, S. W. 2013 Free-surface flow past arbitrary topography and an inverse approach for wave-free solutions. IMA J. Appl. Maths 78, 685–696.Google Scholar
Binder, B. J., Dias, F. & Vanden-Broeck, J. M. 2006 Steady free-surface flow past an uneven channel bottom. Theor. Comput. Fluid Dyn. 20, 125–144.Google Scholar
Binder, B. J. & Vanden-Broeck, J.-M. 2007 The effect of disturbances on the flows under a sluice gate and past an inclined plate. J. Fluid Mech. 576, 475–490.Google Scholar
Burns, J. C. 1953 Long waves in running water. Math. Proc. Camb. Phil. Soc. 49, 695–706.Google Scholar
Buttle, N. R., Pethiyagoda, R., Moroney, T. J. & McCue, S. W. 2018 Three-dimensional free-surface flow over arbitrary bottom topography. J. Fluid Mech. 846, 166–189.Google Scholar
Chen, C.-L. 1991 Unified theory on power laws for flow resistance. J. Hydraul. Engng 117, 371–389.Google Scholar
Cheng, N.-S. 2007 Power-law index for velocity profiles in open channel flows. Adv. Water Resour. 30, 1775–1784.Google Scholar
Chuang, J. M. 2000 Numerical studies on non-linear free surface flow using generalized Schwarz–Christoffel transformation. Intl J. Numer. Meth. Fluids 32, 745–772.Google Scholar
Cole, S. L. 1985 Transient waves produced by flow past a bump. Wave Motion 7, 579–587.Google Scholar
Craik, A. D. D. 1968 Resonant gravity–wave interactions in a shear flow. J. Fluid Mech. 34, 531–549.Google Scholar
Craik, A. D. D. 1970 A wave-interaction model for the generation of windows. J. Fluid Mech. 41, 801–821.Google Scholar
Dias, F. & Vanden-Broeck, J.-M. 1989 Open channel flows with submerged obstructions. J. Fluid Mech. 206, 155–170.Google Scholar
Dias, F. & Vanden-Broeck, J. M. 2002 Generalised critical free-surface flows. J. Engng Maths 42, 291–301.Google Scholar
Djenidi, L., Dubief, Y. & Antonia, R. A. 1997 Advantages of using a power law in a low R 𝜃 turbulent boundary layer. Exp. Fluids 22, 348–350.Google Scholar
Dolcetti, G., Horoshenkov, K. V., Krynkin, A. & Tait, S. J. 2016 Frequency-wavenumber spectrum of the free surface of shallow turbulent flows over a rough boundary. Phys. Fluids 28, 105105.Google Scholar
Drivas, T. D. & Wunsch, S. 2016 Triad resonance between gravity and vorticity waves in vertical shear. Ocean Model. 103, 87–97.Google Scholar
Ellingsen, S. Å. 2016 Oblique waves on a vertically sheared current are rotational. Eur. J. Mech. (B/Fluids) 56, 156–160.Google Scholar
Ellingsen, S. Å. & Li, Y. 2017 Approximate dispersion relations for waves on arbitrary shear flows. J. Geophys. Res. Oceans 122, 9889–9905.Google Scholar
Fenton, J. D. 1973 Some results for surface gravity waves on shear flows. IMA J. Appl. Maths 12, 1–20.Google Scholar
Forbes, L. K. 1988 Critical free-surface flow over a semi-circular obstruction. J. Engng Maths 22, 3–13.Google Scholar
Forbes, L. K. 1989 An algorithm for 3-dimensional free-surface problems in hydrodynamics. J. Comput. Phys. 82, 330–347.Google Scholar
Forbes, L. K. & Schwartz, L. W. 1982 Free-surface flow over a semicircular obstruction. J. Fluid Mech. 114, 299–314.Google Scholar
George, W. K. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.Google Scholar
Gourlay, T. P. 2001 The supercritical bore produced by a high-speed ship in a channel. J. Fluid Mech. 434, 399–409.Google Scholar
Hinze, J. O. 1975 Turbulence, vol. 218, p. 457. McGraw-Hill.Google Scholar
Holliday, D. 1977 On nonlinear interactions in a spectrum of inviscid gravity-capillary surface waves. J. Fluid Mech. 83, 737–749.Google Scholar
Katsis, C. & Akylas, T. R. 1987 On the excitation of long nonlinear water waves by a moving pressure distribution. Part 2. Three-dimensional effects. J. Fluid Mech. 177, 49–65.Google Scholar
Kennedy, J. F. 1963 The mechanics of dunes and antidunes in erodible-bed channels. J. Fluid Mech. 16 (4), 521–544.Google Scholar
King, A. C. & Bloor, M. I. G. 1987 Free-surface flow over a step. J. Fluid Mech. 182, 193–208.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Li, Y. & Ellingsen, S. Å. 2016 Ship waves on uniform shear current at finite depth: wave resistance and critical velocity. J. Fluid Mech. 791, 539–567.Google Scholar
Li, Y. & Ellingsen, S. Å. 2019 A framework for modeling linear surface waves on shear currents in slowly varying waters. J. Geophys. Res. Oceans 124, 2527–2545.Google Scholar
Li, Y., Smeltzer, B. K. & Ellingsen, S. Å. 2019 Transient wave resistance upon a real shear current. Eur. J. Mech. (B/Fluids) 73, 180–192.Google Scholar
Lighthill, M. J. 1953 On the critical Froude number for turbulent flow over a smooth bottom. Math. Proc. Camb. Phil. Soc. 49, 704–706, appendix to Burns (1953).Google Scholar
Lighthill, M. J. 1957 The fundamental solution for small steady three-dimensional disturbances to a two-dimensional parallel shear flow. J. Fluid Mech. 3, 113–144.Google Scholar
Mei, C. C. 1969 Steady free surface flow over wavy bed. J. Engng Mech. Div. 95, 1393–1402.Google Scholar
Mei, C. C. 1986 Radiation of solitons by slender bodies advancing in a shallow channel. J. Fluid Mech. 162, 53–67.Google Scholar
Mizumura, K. 1995 Free-surface profile of open-channel flow with wavy boundary. J. Hydraul. Engng 121, 533–539.Google Scholar
Moisy, F. & Rabaud, M. 2014 Mach-like capillary-gravity wakes. Phys. Rev. E 90, 023009.Google Scholar
Phillips, O. M. 1960 On the dynamics of unsteady gravity waves of finite amplitude. Part 1. The elementary interactions. J. Fluid Mech. 9, 193–217.Google Scholar
Phillips, W. R. C. & Shen, Q. 1996 A family of wave-mean shear interactions and their instability to longitudinal vortex form. Stud. Appl. Maths 96, 143–161.Google Scholar
Phillips, W. R. C., Wu, Z. & Lumley, J. L. 1996 On the formation of longitudinal vortices in a turbulent boundary layer over wavy terrain. J. Fluid Mech. 326, 321–341.Google Scholar
Rayleigh, Lord 1883 The form of standing waves on the surface of running water. Proc. Lond. Math. Soc. 1, 69–78.Google Scholar
Sammarco, P., Mei, C. C. & Trulsen, K. 1994 Nonlinear resonance of free surface waves in a current over a sinusoidal bottom: a numerical study. J. Fluid Mech. 279, 377–405.Google Scholar
Shrira, V. I. 1993 Surface waves on shear currents: solution of the boundary-value problem. J. Fluid Mech. 252, 565–584.Google Scholar
Smeltzer, B. K., Æsøy, E. & Ellingsen, S. Å. 2019 Observation of surface wave patterns modified by sub-surface shear currents. J. Fluid Mech. 873, 508–530.Google Scholar
Stokes, G. G. 1880 Mathematical and Physical Papers, vol. 1. Cambridge University Press.Google Scholar
Thomson, Sir William (Lord Kelvin) 1886 On stationary waves in flowing water. Lond. Edinb. Dubl. Phil. Mag. J. Sci. 22–23, t. xxii, pp. 353, 445, 517 (1886), and t. xxiii, p. 52 (1887).Google Scholar
Vanden-Broeck, J.-M. 1997 Numerical calculations of the free-surface flow under a sluice gate. J. Fluid Mech. 330, 339–347.Google Scholar
West, B. J. 1981 On the Simpler Aspects of Nonlinear Fluctuating Deep Water Gravity Waves (Weak Interaction Theory). Springer.Google Scholar
Wu, T. Y.-T. 1987 Generation of upstream advancing solitons by moving disturbances. J. Fluid Mech. 184, 75–99.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.Google Scholar
Zakharov, V. E. & Ostrovsky, L. A. 2009 Modulation instability: the beginning. Physica D 238 (5), 540–548.Google Scholar
Zakharov, V. E. & Shrira, V. I. 1990 About the formation of angular spectrum of wind waves. Zh. Exper. Teor. Fiz. 98, 1941–1958.Google Scholar
Zhang, Y. & Zhu, S. 1996 Open channel flow past a bottom obstruction. J. Engng Maths 30, 487–499.Google Scholar