Published online by Cambridge University Press: 09 January 2013
A concept which explains unstable modes by resonance between two neutral waves is applied to instability in shear flows with non-uniform potential vorticity distribution. In basic flows where shear instability occurs, a pair of neutral waves which should resonate to form an unstable mode does not exist mathematically unless the basic potential vorticity is uniform, owing to the shear of the basic flow. However, if a small window region is made where the potential vorticity of the basic flow is uniform, regular neutral modes can exist. The neutral wave located at the centre of this window region, which corresponds to a mode where the jump in its first derivative at one end of the window region cancels that at the other end, can be considered to be the hidden neutral wave. It is equivalent to a continuous mode which does not have a jump in its first derivative at the critical point even though it can have a singularity of 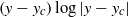 $(y\ensuremath{-} {y}_{c} )\log \vert y\ensuremath{-} {y}_{c} \vert $, in the limit of an infinitely small window region. Thus, a method for retrieving neutral waves hidden in the shear of the basic flow is proposed here. By sweeping the basic flow range with this uniform potential vorticity window, all the features of the hidden neutral wave appear. By applying this method, shear instability in a flow with a tanh-shaped basic velocity profile is well explained via the resonance between neutral waves.
$(y\ensuremath{-} {y}_{c} )\log \vert y\ensuremath{-} {y}_{c} \vert $, in the limit of an infinitely small window region. Thus, a method for retrieving neutral waves hidden in the shear of the basic flow is proposed here. By sweeping the basic flow range with this uniform potential vorticity window, all the features of the hidden neutral wave appear. By applying this method, shear instability in a flow with a tanh-shaped basic velocity profile is well explained via the resonance between neutral waves.