Article contents
Shape optimisation for a stochastic two-dimensional cylinder wake using ensemble variation
Published online by Cambridge University Press: 16 March 2023
Abstract
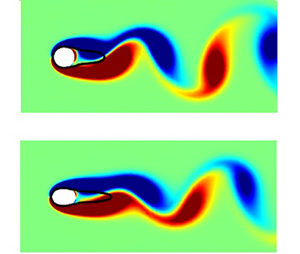
In the present study, the shape of a two-dimensional cylinder is optimised to minimise the mean drag in laminar unsteady flow under a noisy environment. A small inline stochastic oscillation in the free-stream velocity, which follows the Ornstein–Uhlenbeck process, is considered for the noise. The small noise is found to yield a large random fluctuation in instantaneous drag of the cylinder due to the effect of added mass. Subject to the strong random fluctuation of drag, the shape optimisation is performed using an ensemble-variation-based method (EnVar), as the conventional adjoint-based optimisation is not applicable to such a flow environment with unknown free-stream noise. The optimised cylinder geometry is found to be a nearly-symmetric slender oval at a low Reynolds number. As the Reynolds number is increased, two optimal shapes emerge: one is identical to the oval obtained at the low Reynolds number, and the other is an asymmetric oval, the rear side of which is more slender than the front side, reminiscent of an aerofoil. Despite the large random fluctuation in the instantaneous drag, the optimal cylinder shapes obtained for different levels of the upstream noise are found to be almost identical. It is shown that the robust nature of the optimal cylinder shape originates from the limited influence of the small upstream noise on the mean flow properties of the cylinder wake. Finally, the optimised cylinder primarily reduces the pressure component of the drag, associated mainly with vortex shedding in the wake, and this is achieved by marginally increasing the viscous drag through the shape change.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by



