Article contents
Shape dynamics of capsules in two phase-shifted orthogonal ultrasonic standing waves: a numerical investigation
Published online by Cambridge University Press: 30 May 2023
Abstract
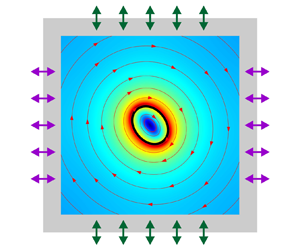
This work investigates the time-averaged shape dynamics of a soft elastic capsule in two phase-shifted orthogonal ultrasonic standing waves. The capsule consists of an elastic membrane that encloses a viscous fluid and is immersed in another viscous fluid. Combining the acoustic perturbation theory of fluid dynamics with the thin-shell mechanics of capsule membrane deformation, two sets of equations are established to govern the ultrasonic propagation and the time-averaged response of the fluid–capsule system, respectively. These governing equations are solved numerically based on the finite element method. Numerical simulations show that the ultrasonic standing waves have pure elongation and pure rotation effects on the initially circular capsule when the phase difference is 0 and  ${\rm \pi}/2$, respectively. By setting the phase difference between 0 and
${\rm \pi}/2$, respectively. By setting the phase difference between 0 and  ${\rm \pi}/2$, it is found that the initially circular capsule exhibits a tank-treading motion due to the combined effect of the elongation and rotation. The capsule membrane elasticity and internal fluid viscosity have significant effects on the tank-treading behaviour of the initially circular capsule, including elongation deformation, inclination angle and tank-treading velocity. For the initially non-circular capsule, three types of dynamical states, including stable orientation, swinging and tumbling, are predicted by varying the phase difference and intensity of the ultrasonic standing waves, as well as the initial shape, membrane elasticity and internal fluid viscosity of the initially non-circular capsule. This work enriches the cell manipulation capabilities of ultrasonic standing wave micro-acoustofluidics and may inspire new biological applications.
${\rm \pi}/2$, it is found that the initially circular capsule exhibits a tank-treading motion due to the combined effect of the elongation and rotation. The capsule membrane elasticity and internal fluid viscosity have significant effects on the tank-treading behaviour of the initially circular capsule, including elongation deformation, inclination angle and tank-treading velocity. For the initially non-circular capsule, three types of dynamical states, including stable orientation, swinging and tumbling, are predicted by varying the phase difference and intensity of the ultrasonic standing waves, as well as the initial shape, membrane elasticity and internal fluid viscosity of the initially non-circular capsule. This work enriches the cell manipulation capabilities of ultrasonic standing wave micro-acoustofluidics and may inspire new biological applications.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by



