Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-27T02:26:03.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Shape design for stabilizing microparticles in inertial microfluidic flows

Published online by Cambridge University Press:  14 January 2020

Aditya Kommajosula Open the ORCID record for Aditya Kommajosula [Opens in a new window] ,
Daniel Stoecklein ,
Dino Di Carlo  and
Baskar Ganapathysubramanian
Aditya Kommajosula
Affiliation:
Department of Mechanical Engineering, Iowa State University, Ames, IA50011, USA
Daniel Stoecklein
Affiliation:
Department of Bioengineering, University of California, Los Angeles, CA90095, USA
Dino Di Carlo
Affiliation:
Department of Bioengineering, University of California, Los Angeles, CA90095, USA
Baskar Ganapathysubramanian*
Affiliation:
Department of Mechanical Engineering, Iowa State University, Ames, IA50011, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Design of isolated microparticles which stabilize at the centreline of a channel flow is examined numerically, for moderate Reynolds numbers ($10\leqslant Re\leqslant 80$). This problem is motivated by the need for the design of shaped particle carriers for use in next generation microfluidic cell analysis devices. Stability metrics for particles with arbitrary shapes are formulated based on linear stability theory. Particle shape is parametrized by a compact, non-uniform rational B-spline-based representation. Shape design is posed as an optimization problem and solved using adaptive Bayesian optimization. We focus on designing particles for stability at the channel centreline robust to perturbations. Our results indicate that centreline focusing particles are families of characteristic ‘fish’/‘bottle’/‘dumbbell’-like shapes, exhibiting fore–aft asymmetry. A parametric exploration is then performed to identify stable particle designs at different $k$ values (particle chord-to-channel width ratio) and $Re$ values ($0.1\leqslant k\leqslant 0.4,10\leqslant Re\leqslant 80$). Particles at high $k$ values and $Re$ values are highly stabilized when compared to those at low $k$ values and $Re$ values. We validate the performance of designed particles to perturbations in flow using detailed fluid–structure interaction simulations over different $k$ values and $Re$ values. We identify a basin of attraction around the centreline, within which any arbitrary release results in rotationally stable centreline focusing. We find that this basin spans larger release angle ranges and lateral locations (tending to the channel width) for narrower channels. This effectively standardizes the notion of global focusing using the current stability paradigm in narrow channels, which eliminates the need for an independent design for global focusing in such configurations. The framework detailed in this work is illustrated for two-dimensional cases and is generalizable to stability in three-dimensional flow fields. The current formulation is agnostic to $Re$ and particle/channel geometry, which indicates substantial potential for integration with imaging flow cytometry tools and microfluidic biosensing assays.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Mathematical Foundations: Computational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 886 , 10 March 2020 , A14
Copyright
© 2020 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmolov, E. S. 1999 The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 381, 63–87.CrossRefGoogle Scholar
Bingol, O. R. & Krishnamurthy, A. 2019 NURBS-Python: An open-source object-oriented NURBS modeling framework in Python. SoftwareX 9, 85–94.CrossRefGoogle Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14 (1956), 284–304.CrossRefGoogle Scholar
Chwang, A. T. 1975 Hydromechanics of low-Reynolds-number flow. Part 3. Motion of a spheroidal particle in quadratic flows. J. Fluid Mech. 72 (01), 17.CrossRefGoogle Scholar
Coclite, A., de Tullio, M. D., Pascazio, G. & Decuzzi, P. 2016 A combined lattice Boltzmann and immersed boundary approach for predicting the vascular transport of differently shaped particles. Comput. Fluids 136, 260–271.CrossRefGoogle Scholar
Crowe, C. T., Chung, J. N. & Troutt, T. R. 1988 Particle mixing in free shear flows. Prog. Energy Combust. Sci. 14 (3), 171–194.CrossRefGoogle Scholar
Dendukuri, D., Gu, S. S., Pregibon, D. C., Hatton, T. A. & Doyle, P. S. 2007 Stop-flow lithography in a microfluidic device. Lab on a Chip 7 (7), 818–828.CrossRefGoogle Scholar
Di Carlo, D. 2009 Inertial microfluidics. Lab on a Chip 9 (21), 3038–3046.CrossRefGoogle ScholarPubMed
Di Carlo, D., Edd, J. F., Humphry, K. J., Stone, H. A. & Toner, M. 2009 Particle segregation and dynamics in confined flows. Phys. Rev. Lett. 102 (9), 094503.CrossRefGoogle ScholarPubMed
Dupire, J., Socol, M. & Viallat, A. 2012 Full dynamics of a red blood cell in shear flow. Proc. Natl Acad. Sci. USA 109 (51), 20808–20813.CrossRefGoogle ScholarPubMed
Einarsson, J., Mihiretie, B. M., Laas, A., Ankardal, S., Angilella, J. R., Hanstorp, D. & Mehlig, B. 2016 Tumbling of asymmetric microrods in a microchannel flow. Phys. Fluids 28 (1), 013302.CrossRefGoogle Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010 A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 98 (10), 2215–2225.CrossRefGoogle ScholarPubMed
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 1. Sedimentation. J. Fluid Mech. 261, 95–134.CrossRefGoogle Scholar
Feng, J., Huang, P. Y. & Joseph, D. D. 1995 Dynamic simulation of the motion of capsules in pipelines. J. Fluid Mech. 286, 201–227.CrossRefGoogle Scholar
Forrester, A., Sobester, A. & Keane, A. 2008 Engineering Design via Surrogate Modelling: A Practical Guide. John Wiley & Sons.CrossRefGoogle Scholar
Golden, J. P., Kim, J. S., Erickson, J. S., Hilliard, L. R., Howell, P. B., Anderson, G. P., Nasir, M. & Ligler, F. S. 2009 Multi-wavelength microflow cytometer using groove-generated sheath flow. Lab on a Chip 9 (13), 1942–1950.CrossRefGoogle ScholarPubMed
Hood, K., Lee, S. & Roper, M. 2015 Inertial migration of a rigid sphere in three-dimensional Poiseuille flow. J. Fluid Mech. 765, 452–479.CrossRefGoogle Scholar
Hughes, T. J. R., Cottrell, J. A. & Bazilevs, Y. 2005 Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Meth. Appl. Mech. Engng 194 (39-41), 4135–4195.CrossRefGoogle Scholar
Hur, S. C., Choi, S.-E., Kwon, S. & Carlo, D. D. 2011 Inertial focusing of non-spherical microparticles. Appl. Phys. Lett. 99 (4), 044101.CrossRefGoogle Scholar
Kilimnik, A., Mao, W. & Alexeev, A. 2011 Inertial migration of deformable capsules in channel flow. Phys. Fluids 23 (12), 123302.CrossRefGoogle Scholar
Kim, J.-A., Lee, J., Wu, C., Nam, S., Di Carlo, D. & Lee, W. 2016 Inertial focusing in non-rectangular cross-section microchannels and manipulation of accessible focusing positions. Lab on a Chip 16 (6), 992–1001.CrossRefGoogle ScholarPubMed
Kommajosula, A., Kim, J., Lee, W. & Ganapathysubramanian, B.2019 High-throughput, automated prediction of focusing-patterns for inertial microfluidics. arXiv:1901.05561.Google Scholar
Lee, W., Amini, H., Stone, H. A. & Di Carlo, D. 2010 Dynamic self-assembly and control of microfluidic particle crystals. Proc. Natl Acad. Sci. USA 107 (52), 22413–22418.CrossRefGoogle ScholarPubMed
Leith, D. 1987 Drag on nonspherical objects. Aerosol Sci. Technol. 6 (2), 153–161.CrossRefGoogle Scholar
McLaughlin, J. B. 1993 The lift on a small sphere in wall-bounded linear shear flows. J. Fluid Mech. 246, 249–265.CrossRefGoogle Scholar
Nitta, N., Sugimura, T., Isozaki, A., Mikami, H., Hiraki, K., Sakuma, S., Iino, T., Arai, F., Endo, T., Fujiwaki, Y. et al. 2018 Intelligent image-activated cell sorting. Cell 175 (1), 266–276.CrossRefGoogle ScholarPubMed
Oberbeck, A. 1876 Ueber stationäre Flüssigkeitsbewegungen mit Berücksichtigung der inneren Reibung. J. für die reine und angewandte Mathematik 81, 62–80.Google Scholar
Paulsen, K.2017 Complex-shaped particle fabrication from inertial microfluidics. PhD thesis, Rensselaer Polytechnic Institute, Troy, NY.Google Scholar
Paulsen, K. S., Di Carlo, D. & Chung, A. J. 2015 Optofluidic fabrication for 3D-shaped particles. Nature Commun. 6, 6976.CrossRefGoogle ScholarPubMed
Pham, D. T. & Gault, R. S. 1998 A comparison of rapid prototyping technologies. Intl J. Machine Tools Manufacture 38 (10–11), 1257–1287.CrossRefGoogle Scholar
Piva, M. F. & Gabbanelli, S. 2003 A single dumbbell falling under gravity in a cellular flow field. J. Phys. A: Math. Gen. 36 (15), 4291.Google Scholar
Piva, M. F. & Martino, G. R. 2008 A rigid dumbbell settling under gravity in a periodic flow field. J. Phys. A: Math. Theor. 42 (2), 025501.Google Scholar
Pokuri, B. S. S., Lofquist, A., Risko, C. M. & Ganapathysubramanian, B.2018 PARyOpt: a software for Parallel Asynchronous Remote Bayesian Optimization. arXiv:1809.04668.Google Scholar
Prakash, S., Pinti, M. & Bhushan, B. 2012 Theory, fabrication and applications of microfluidic and nanofluidic biosensors. Phil. Trans. R. Soc. Lond. A 370 (1967), 2269–2303.Google ScholarPubMed
Saffman, P. G. T. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.CrossRefGoogle Scholar
Segre, G. & Silberberg, A. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210.CrossRefGoogle Scholar
Segré, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 2. Experimental results and interpretation. J. Fluid Mech. 14 (1), 136–157.CrossRefGoogle Scholar
Shaw, L. A., Chizari, S., Shusteff, M., Naghsh-Nilchi, H., Di Carlo, D. & Hopkins, J. B. 2018 Scanning two-photon continuous flow lithography for synthesis of high-resolution 3D microparticles. Opt. Express 26 (10), 13543–13548.CrossRefGoogle ScholarPubMed
Singh, V., Koch, D. L. & Stroock, A. D. 2013 Rigid ring-shaped particles that align in simple shear flow. J. Fluid Mech. 722, 121–158.CrossRefGoogle Scholar
Singh, V., Koch, D. L., Subramanian, G. & Stroock, A. D. 2014 Rotational motion of a thin axisymmetric disk in a low Reynolds number linear flow. Phys. Fluids 26 (3), 033303.CrossRefGoogle Scholar
Strogatz, S. H. 2018 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. CRC Press.CrossRefGoogle Scholar
Tam, C. K. W. & Hyman, W. A. 1973 Transverse motion of an elastic sphere in a shear field. J. Fluid Mech. 59 (1), 177–185.CrossRefGoogle Scholar
Thaokar, R. M., Schiessel, H. & Kulic, I. M. 2007 Hydrodynamics of a rotating torus. Eur. Phys. J. B 60 (3), 325–336.CrossRefGoogle Scholar
de Tullio, M. D., Pascazio, G. & Napolitano, M. 2012 Arbitrarily shaped particles in shear flow. In Proceedings Seventh International Conference on Computational Fluid Dynamics (ICCFD7), Big Island, HI, USA.Google Scholar
Uspal, W. E. & Doyle, P. S. 2014 Self-organizing microfluidic crystals. Soft Matt. 10 (28), 5177–5191.CrossRefGoogle ScholarPubMed
Wen, B., Chen, H., Qin, Z., He, B. & Zhang, C. 2016 Lateral migration and nonuniform rotation of suspended ellipse in Poiseuille flow. Comput. Math. Appl 78 (4), 1142–1153.CrossRefGoogle Scholar
William, E., Eral, H. B. & Doyle, P. S. 2013 Engineering particle trajectories in microfluidic flows using particle shape. Nature Commun. 4.Google Scholar
Wu, C.-Y., Stoecklein, D., Kommajosula, A., Lin, J., Owsley, K., Ganapathysubramanian, B. & Di Carlo, D. 2018 Shaped 3D microcarriers for adherent cell culture and analysis. Microsystems Nanoengineering 4 (1), 21.CrossRefGoogle ScholarPubMed
Xu, S., Xu, F., Kommajosula, A., Hsu, M.-C. & Ganapathysubramanian, B. 2019 Immersogeometric analysis of moving objects in incompressible flows. Comput. Fluids 189, 24–33.CrossRefGoogle Scholar
Yamada, M., Nakashima, M. & Seki, M. 2004 Pinched flow fractionation: continuous size separation of particles utilizing a laminar flow profile in a pinched microchannel. Analyt. Chem. 76 (18), 5465–5471.CrossRefGoogle Scholar
Yang, B. H., Wang, J., Joseph, D. D., Hu, H. H., Pan, T.-W. & Glowinski, R. 2005 Migration of a sphere in tube flow. J. Fluid Mech. 540, 109–131.CrossRefGoogle Scholar
Yang, B. H., Wang, J., Joseph, D. D., Hu, H. H., Pan, T.-W. & Glowinski, R. 2006 Numerical study of particle migration in tube and plane Poiseuille flows. In IUTAM Symposium on Computational Approaches to Multiphase Flow (ed. Balachandar, S. & Prosperetti, A.), vol. 81, pp. 225–235. Springer.CrossRefGoogle Scholar
Yuan, R., Nagarajan, M. B., Lee, J., Voldman, J., Doyle, P. S. & Fink, Y. 2018 Designable 3D microshapes fabricated at the intersection of structured flow and optical fields. Small 14 (50), 1803585.CrossRefGoogle ScholarPubMed
Zhang, J., Yan, S., Yuan, D., Alici, G., Nguyen, N.-T., Warkiani, M. E. & Li, W. 2016 Fundamentals and applications of inertial microfluidics: a review. Lab on a Chip 16 (1), 10–34.CrossRefGoogle ScholarPubMed

Kommajosula et al. supplementary movie 1

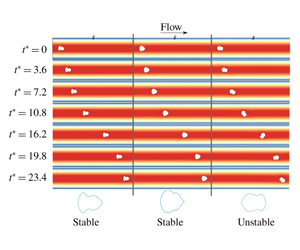
Long channel FSI simulation for highly stable particle at Re = 20, k = 0.3 (angular perturbation)

Download Kommajosula et al. supplementary movie 1(Video)
Video 4.7 MB

Kommajosula et al. supplementary movie 2

Long channel FSI simulation for weakly stable particle at Re = 20, k = 0.3 (angular perturbation)

Download Kommajosula et al. supplementary movie 2(Video)
Video 5.8 MB

Kommajosula et al. supplementary movie 3

Long channel FSI simulation for unstable particle at Re = 20, k = 0.3 (angular perturbation)

Download Kommajosula et al. supplementary movie 3(Video)
Video 5.9 MB

Kommajosula et al. supplementary movie 4

Long channel FSI simulation for stable particle at Re = 20, k = 0.4 (angular perturbation)

Download Kommajosula et al. supplementary movie 4(Video)
Video 3.1 MB

Kommajosula et al. supplementary movie 5

Long channel FSI simulation for unstable particle at Re = 20, k = 0.4 (angular perturbation)

Download Kommajosula et al. supplementary movie 5(Video)
Video 3 MB

Kommajosula et al. supplementary movie 6

Long channel FSI simulation for stable particle at Re = 80, k = 0.4 (angular perturbation)

Download Kommajosula et al. supplementary movie 6(Video)
Video 1.2 MB

Kommajosula et al. supplementary movie 7

Long channel FSI simulation for unstable particle at Re = 80, k = 0.4 (angular perturbation)

Download Kommajosula et al. supplementary movie 7(Video)
Video 1.3 MB

Kommajosula et al. supplementary movie 8

Long channel FSI simulation for stable particle-1 at Re = 20, k = 0.7 (lateral perturbation)

Download Kommajosula et al. supplementary movie 8(Video)
Video 1.6 MB

Kommajosula et al. supplementary movie 9

Long channel FSI simulation for stable particle-2 at Re = 20, k = 0.7 (lateral perturbation)

Download Kommajosula et al. supplementary movie 9(Video)
Video 1.6 MB

Kommajosula et al. supplementary movie 10

Long channel FSI simulation for unstable particle at Re = 20, k = 0.7 (lateral perturbation)

Download Kommajosula et al. supplementary movie 10(Video)
Video 1.7 MB