Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fernando, H. J. S.
Pardyjak, E. R.
Di Sabatino, S.
Chow, F. K.
De Wekker, S. F. J.
Hoch, S. W.
Hacker, J.
Pace, J. C.
Pratt, T.
Pu, Z.
Steenburgh, W. J.
Whiteman, C. D.
Wang, Y.
Zajic, D.
Balsley, B.
Dimitrova, R.
Emmitt, G. D.
Higgins, C. W.
Hunt, J. C. R.
Knievel, J. C.
Lawrence, D.
Liu, Y.
Nadeau, D. F.
Kit, E.
Blomquist, B. W.
Conry, P.
Coppersmith, R. S.
Creegan, E.
Felton, M.
Grachev, A.
Gunawardena, N.
Hang, C.
Hocut, C. M.
Huynh, G.
Jeglum, M. E.
Jensen, D.
Kulandaivelu, V.
Lehner, M.
Leo, L. S.
Liberzon, D.
Massey, J. D.
McEnerney, K.
Pal, S.
Price, T.
Sghiatti, M.
Silver, Z.
Thompson, M.
Zhang, H.
and
Zsedrovits, T.
2015.
The MATERHORN: Unraveling the Intricacies of Mountain Weather.
Bulletin of the American Meteorological Society,
Vol. 96,
Issue. 11,
p.
1945.
Stiperski, Ivana
and
Rotach, Mathias W.
2016.
On the Measurement of Turbulence Over Complex Mountainous Terrain.
Boundary-Layer Meteorology,
Vol. 159,
Issue. 1,
p.
97.
Klipp, Cheryl
2018.
Turbulent Friction Velocity Calculated from the Reynolds Stress Tensor.
Journal of the Atmospheric Sciences,
Vol. 75,
Issue. 4,
p.
1029.
Dimitrieva, N. F.
and
Chashechkin, Yu. D.
2018.
Fine Structure of a Stratified Flow around a Fixed and Slow-Moving Wedge.
Oceanology,
Vol. 58,
Issue. 3,
p.
340.
Hilel Goldshmid, Roni
Bardoel, Stef L.
Hocut, Christopher M.
Zhong, Qiang
Liberzon, Dan
and
Fernando, Harindra J. S.
2018.
Separation of Upslope Flow over a Plateau.
Atmosphere,
Vol. 9,
Issue. 5,
p.
165.
Serafin, Stefano
Adler, Bianca
Cuxart, Joan
De Wekker, Stephan
Gohm, Alexander
Grisogono, Branko
Kalthoff, Norbert
Kirshbaum, Daniel
Rotach, Mathias
Schmidli, Jürg
Stiperski, Ivana
Večenaj, Željko
and
Zardi, Dino
2018.
Exchange Processes in the Atmospheric Boundary Layer Over Mountainous Terrain.
Atmosphere,
Vol. 9,
Issue. 3,
p.
102.
Zhai, Haoyu
Xu, Feng
Saha, Suvash C.
and
Hou, Yudong
2018.
Natural convection and heat transfer on a section-triangular roof.
International Communications in Heat and Mass Transfer,
Vol. 92,
Issue. ,
p.
23.
Dimitrieva, N.
2019.
Flows around a 2D horizontal wedge in a steadily stratified liquid.
Hydrodynamics and Acoustics,
Vol. 1,
Issue. 3,
p.
316.
Zhai, Haoyu
Nie, Bingchuan
Chen, Bo
and
Xu, Feng
2019.
Unsteady flows on a roof imposed by a periodic heat flux: 2D simulation and scaling analysis.
International Journal of Thermal Sciences,
Vol. 145,
Issue. ,
p.
106002.
Throneberry, Glen
Hocut, Christopher M.
Shu, Fangjun
and
Abdelkefi, Abdessattar
2019.
Multi-rotor wake propagation investigation for atmospheric sampling.
Hilel Goldshmid, Roni
and
Liberzon, Dan
2020.
Obtaining turbulence statistics of thermally driven anabatic flow by sonic-hot-film combo anemometer.
Environmental Fluid Mechanics,
Vol. 20,
Issue. 5,
p.
1221.
Pirro, A.
Fernando, H.J.S.
Wijesekera, H.W.
Jensen, T.G.
Centurioni, L.R.
and
Jinadasa, S.U.P.
2020.
Eddies and currents in the Bay of Bengal during summer monsoons.
Deep Sea Research Part II: Topical Studies in Oceanography,
Vol. 172,
Issue. ,
p.
104728.
Radünz, William Corrêa
Sakagami, Yoshiaki
Haas, Reinaldo
Petry, Adriane Prisco
Passos, Júlio César
Miqueletti, Mayara
and
Dias, Eduardo
2020.
The variability of wind resources in complex terrain and its relationship with atmospheric stability.
Energy Conversion and Management,
Vol. 222,
Issue. ,
p.
113249.
Repina, Irina А.
Shestakova, Anna А.
Bedanokov, Murat K.
Berzegova, Roza B.
and
Lebedev, Sergey A.
2021.
The Republic of Adygea Environment.
Vol. 106,
Issue. ,
p.
359.
Zhai, Haoyu
Torres, Juan F.
Zhao, Yongling
and
Xu, Feng
2021.
Transition from steady to chaotic flow of natural convection on a section-triangular roof.
Physical Review Fluids,
Vol. 6,
Issue. 1,
Payne, Cory M.
Passner, Jeffrey E.
Dumais, Robert E.
Abdelkefi, Abdessattar
and
Hocut, Christopher M.
2021.
Presence of Longitudinal Roll Structures during Synoptic Forced Conditions in Complex Terrain.
Atmosphere,
Vol. 12,
Issue. 6,
p.
737.
Cintolesi, Carlo
Di Santo, Dario
Barbano, Francesco
and
Di Sabatino, Silvana
2021.
Anabatic Flow along a Uniformly Heated Slope Studied through Large-Eddy Simulation.
Atmosphere,
Vol. 12,
Issue. 7,
p.
850.
Radünz, William Corrêa
Sakagami, Yoshiaki
Haas, Reinaldo
Petry, Adriane Prisco
Passos, Júlio César
Miqueletti, Mayara
and
Dias, Eduardo
2021.
Influence of atmospheric stability on wind farm performance in complex terrain.
Applied Energy,
Vol. 282,
Issue. ,
p.
116149.
Farina, Sofia
and
Zardi, Dino
2023.
Understanding Thermally Driven Slope Winds: Recent Advances and Open Questions.
Boundary-Layer Meteorology,
Vol. 189,
Issue. 1-3,
p.
5.
Dumais, Robert E.
Spade, Daniela M.
and
Gill, Thomas E.
2023.
Simulations of Mesoscale Flow Systems around Dugway Proving Ground Using the WRF Modeling System.
Atmosphere,
Vol. 14,
Issue. 2,
p.
251.
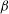 ${\it\beta}$ larger than a critical value
${\it\beta}$ larger than a critical value 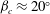 ${\it\beta}_{c}\approx 20^{\circ }$, the separated flow generated a rising plume completely fed by the anterior upslope flow. For this case, a simple model based on a balance between the opposing vorticities of baroclinicity and shear was proposed to predict the location of the separation point relative to the mountain base. The model also predicts the velocity and length scales at separation as well as those of the rising plume after separation. In the second regime,
${\it\beta}_{c}\approx 20^{\circ }$, the separated flow generated a rising plume completely fed by the anterior upslope flow. For this case, a simple model based on a balance between the opposing vorticities of baroclinicity and shear was proposed to predict the location of the separation point relative to the mountain base. The model also predicts the velocity and length scales at separation as well as those of the rising plume after separation. In the second regime, 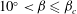 $10^{\circ }<{\it\beta}\leqslant {\it\beta}_{c}$, the volume flow of the separated plume was not fully supplied by the upslope flow, requiring entrainment of additional ambient fluid at the base of the plume source. The third regime occurred when
$10^{\circ }<{\it\beta}\leqslant {\it\beta}_{c}$, the volume flow of the separated plume was not fully supplied by the upslope flow, requiring entrainment of additional ambient fluid at the base of the plume source. The third regime occurred when 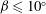 ${\it\beta}\leqslant 10^{\circ }$, wherein the plume almost completely engulfed the slope, similar to a buoyant plume emanating from a source of finite dimensions, thus overshadowing the upslope flow. Measurements of the separation point conducted during the MATERHORN field research program were consistent with the results of the laboratory experiments and modelling.
${\it\beta}\leqslant 10^{\circ }$, wherein the plume almost completely engulfed the slope, similar to a buoyant plume emanating from a source of finite dimensions, thus overshadowing the upslope flow. Measurements of the separation point conducted during the MATERHORN field research program were consistent with the results of the laboratory experiments and modelling.


