1 Introduction
Turbulent boundary-layer separation has an immediate impact on the aerodynamic performance of high-speed vehicles and is an intrinsically unsteady phenomenon. At supersonic speeds, it is commonly induced by adverse pressure gradients in regions of surface deflection or interference – e.g. flaps, fins, protuberances – as well as by the impingement of external shocks originating in other parts of the vehicle. The separated high-speed boundary layer is in strong interaction with the shock structure, arising from the local deflection of the separating and reattaching flow, with a further incident shock in cases where that is the cause of separation. Regions of shock-wave/turbulent-boundary-layer interaction (STBLI) whereby a strong adverse pressure gradient induces separation are typically associated with drastic variations in surface flow properties, including local enhancements in pressure and heat transfer, and are of particular complexity given the turbulent nature of the flow. More details on the different forms in which these interactions may in practice take place can be found in Babinsky & Harvey (Reference Babinsky and Harvey2014).
While upstream turbulent boundary-layer time scales are typically large – with frequencies of order of the ratio of edge velocity to boundary-layer thickness
![]() $O(U_{e}/\unicode[STIX]{x1D6FF}_{o})$
– STBLIs involving separation have been widely documented to exhibit frequencies approximately three to two orders of magnitude lower,
$O(U_{e}/\unicode[STIX]{x1D6FF}_{o})$
– STBLIs involving separation have been widely documented to exhibit frequencies approximately three to two orders of magnitude lower,
![]() $O((10^{-3}-10^{-2})U_{e}/\unicode[STIX]{x1D6FF}_{o})$
. A number of sources have been suggested as the origin of their low-frequency unsteadiness but there is no clear consensus on their cause, in part due to the somewhat disparate findings when contrasting the variety of configurations and flow conditions across studies (Gaitonde Reference Gaitonde2015). This broadly leads to undesired unknowns in aerodynamic design, whereby flow unsteadiness, e.g. on control surfaces or even leading to fatigue and with the potential of approaching structural resonance, may require special scrutiny (e.g. Sandham Reference Sandham2011).
$O((10^{-3}-10^{-2})U_{e}/\unicode[STIX]{x1D6FF}_{o})$
. A number of sources have been suggested as the origin of their low-frequency unsteadiness but there is no clear consensus on their cause, in part due to the somewhat disparate findings when contrasting the variety of configurations and flow conditions across studies (Gaitonde Reference Gaitonde2015). This broadly leads to undesired unknowns in aerodynamic design, whereby flow unsteadiness, e.g. on control surfaces or even leading to fatigue and with the potential of approaching structural resonance, may require special scrutiny (e.g. Sandham Reference Sandham2011).
Early literature on STBLI unsteadiness is often found to look into whether the low-frequency pulsations are driven by incoming turbulence or via an upstream feedback mechanism through the subsonic separation region; a detailed account on some of the main arguments may be found in the review by Dolling (Reference Dolling2001), and more recently by Clemens & Narayanaswamy (Reference Clemens and Narayanaswamy2014), amongst others. Both influences have been extensively documented in past experimental and numerical studies and may be expected to be always at play to some extent. On the one hand, incoming turbulence is an unequivocal source of unsteadiness and a link between upstream fluctuations associated with turbulent superstructures, with a typical length
![]() ${\sim}30\unicode[STIX]{x1D6FF}_{o}$
, and low-frequency separation-shock motions has been noted in weakly separated flows at relatively high Reynolds numbers
${\sim}30\unicode[STIX]{x1D6FF}_{o}$
, and low-frequency separation-shock motions has been noted in weakly separated flows at relatively high Reynolds numbers
![]() $Re_{\unicode[STIX]{x1D6FF}}\approx 5\times 10^{5}$
(Ganapathisubramani, Clemens & Dolling Reference Ganapathisubramani, Clemens and Dolling2007, Reference Ganapathisubramani, Clemens and Dolling2009; Humble et al.
Reference Humble, Elsinga, Scarano and Van Oudheusden2009), where
$Re_{\unicode[STIX]{x1D6FF}}\approx 5\times 10^{5}$
(Ganapathisubramani, Clemens & Dolling Reference Ganapathisubramani, Clemens and Dolling2007, Reference Ganapathisubramani, Clemens and Dolling2009; Humble et al.
Reference Humble, Elsinga, Scarano and Van Oudheusden2009), where
![]() $Re_{\unicode[STIX]{x1D6FF}}=U_{e}\unicode[STIX]{x1D6FF}_{o}/\unicode[STIX]{x1D708}_{e}$
and
$Re_{\unicode[STIX]{x1D6FF}}=U_{e}\unicode[STIX]{x1D6FF}_{o}/\unicode[STIX]{x1D708}_{e}$
and
![]() $\unicode[STIX]{x1D708}_{e}$
is kinematic viscosity at the boundary-layer edge. Similar turbulent superstructures have been documented in subsonic boundary layers (e.g. Kim & Adrian Reference Kim and Adrian1999, Adrian, Meinhart & Tomkins Reference Adrian, Meinhart and Tomkins2000) and, within the current limitations on their scaling and statistical behaviour, it seems plausible they could excite the interaction at frequencies of order
$\unicode[STIX]{x1D708}_{e}$
is kinematic viscosity at the boundary-layer edge. Similar turbulent superstructures have been documented in subsonic boundary layers (e.g. Kim & Adrian Reference Kim and Adrian1999, Adrian, Meinhart & Tomkins Reference Adrian, Meinhart and Tomkins2000) and, within the current limitations on their scaling and statistical behaviour, it seems plausible they could excite the interaction at frequencies of order
![]() $O((10^{-2}-10^{-1})U_{e}/\unicode[STIX]{x1D6FF}_{o})$
.
$O((10^{-2}-10^{-1})U_{e}/\unicode[STIX]{x1D6FF}_{o})$
.
Other cases to have instead sustained the dominance of a downstream mechanism include the Mach 2.3 incident shock STBLI experiments by Dupont, Haddad & Debiève (Reference Dupont, Haddad and Debiève2006), at relatively lower Reynolds numbers (
![]() $Re_{\unicode[STIX]{x1D6FF}}\approx 5\times 10^{4}$
), and where a shift from high to medium frequencies over approximately the first half of the recirculation was attributed to the development of a shear layer. Stemming from these observations, Piponniau et al. (Reference Piponniau, Dussauge, Debiève and Dupont2009) went on to propose a model which described low-frequency pulsations through a mechanism of bubble breathing countering the shear layer’s entrainment. Both the upstream and downstream influences above were evaluated for varying interaction strengths in the particle image velocimetry experiments by Humble, Scarano & van Oudheusden (Reference Humble, Scarano and Van Oudheusden2009) and Souverein et al. (Reference Souverein, Dupont, Debiève, Dussauge, Van Oudheusden and Scarano2010). The latter observed a correlation with incoming fluctuations, with velocity conditionally higher by approximately
$Re_{\unicode[STIX]{x1D6FF}}\approx 5\times 10^{4}$
), and where a shift from high to medium frequencies over approximately the first half of the recirculation was attributed to the development of a shear layer. Stemming from these observations, Piponniau et al. (Reference Piponniau, Dussauge, Debiève and Dupont2009) went on to propose a model which described low-frequency pulsations through a mechanism of bubble breathing countering the shear layer’s entrainment. Both the upstream and downstream influences above were evaluated for varying interaction strengths in the particle image velocimetry experiments by Humble, Scarano & van Oudheusden (Reference Humble, Scarano and Van Oudheusden2009) and Souverein et al. (Reference Souverein, Dupont, Debiève, Dussauge, Van Oudheusden and Scarano2010). The latter observed a correlation with incoming fluctuations, with velocity conditionally higher by approximately
![]() $4\,\%U_{e}$
when the bubble was contracted for weakly separated interactions
$4\,\%U_{e}$
when the bubble was contracted for weakly separated interactions
![]() $L/\unicode[STIX]{x1D6FF}_{o}\approx 2.2$
(where
$L/\unicode[STIX]{x1D6FF}_{o}\approx 2.2$
(where
![]() $L$
is separation length); stronger separations, with
$L$
is separation length); stronger separations, with
![]() $L/\unicode[STIX]{x1D6FF}_{o}\approx 4.2$
and 6.5, instead exhibited a poorer link (
$L/\unicode[STIX]{x1D6FF}_{o}\approx 4.2$
and 6.5, instead exhibited a poorer link (
![]() ${\sim}1\,\%U_{e}$
) and suggested the dominance of a stronger downstream mechanism.
${\sim}1\,\%U_{e}$
) and suggested the dominance of a stronger downstream mechanism.

Figure 1. Schlieren image of highly separated axisymmetric step STBLI (
![]() $h=22.5~\text{mm}$
,
$h=22.5~\text{mm}$
,
![]() $\unicode[STIX]{x1D6FF}_{o}=3.8~\text{mm}$
), at
$\unicode[STIX]{x1D6FF}_{o}=3.8~\text{mm}$
), at
![]() $M_{e}=3.9$
and
$M_{e}=3.9$
and
![]() $Re_{e}=6.1\times 10^{7}~\text{m}^{-1}$
. Upstream separation and reattachment indicated as
$Re_{e}=6.1\times 10^{7}~\text{m}^{-1}$
. Upstream separation and reattachment indicated as
![]() $S_{1}$
(
$S_{1}$
(
![]() $X_{U}^{\ast }=0$
),
$X_{U}^{\ast }=0$
),
![]() $R_{1}$
(
$R_{1}$
(
![]() $X_{U}^{\ast }=1$
) and respective downstream locations as
$X_{U}^{\ast }=1$
) and respective downstream locations as
![]() $S_{2}$
(
$S_{2}$
(
![]() $X_{D}^{\ast }=0$
),
$X_{D}^{\ast }=0$
),
![]() $R_{2}$
(
$R_{2}$
(
![]() $X_{D}^{\ast }=1$
).
$X_{D}^{\ast }=1$
).
Recent numerical studies appear to have increasingly pointed at a dominant downstream influence via different mechanisms. The direct numerical simulation (DNS) studies by Pirozzoli & Grasso (Reference Pirozzoli and Grasso2006), considering a similar incident shock case as that above, noted bubble instabilities at specific tones likely attributable to Rossiter modes of the local cavity effect, which were in turn suggested to act through acoustic feedback on interaction unsteadiness. Later DNS by Priebe & Martin (Reference Priebe and Martin2012), on a Mach 2.9 compression corner interaction, further documented a correlation between a flapping of the reattachment line and separation shock motions, sustaining the dominance of a downstream forcing mechanism as well. In more recent analysis by Priebe et al. (Reference Priebe, Tu, Rowley and Martin2016), Görtler-type vortices associated with local centrifugal forces in the separated flow were also suggested to play an important role in interaction unsteadiness. An alternate view may be found in the numerical studies by Touber & Sandham (Reference Touber and Sandham2011), which modelled the STBLI as a reduced-order dynamical system and noted a low-frequency global instability mode when the upstream boundary layer was simulated as a white-noise spectrum, i.e. without the need for incoming long coherent structures; when applying a high-pass filter on the boundary layer, low-frequency bubble pulsations were instead found to be suppressed. From this, it was suggested that the coupled boundary-layer/separation-shock system may effectively act as a low-pass filter, possibly driven by low-frequency fluctuations at the natural frequency of the system (be it as broadband environmental noise, or as coherent or incoherent fluctuations). The view of the STBLI as a forced dynamical system is common to most of these different mechanisms and studies seem to generally point at a reduced influence of the upstream boundary layer in stronger interactions, for separation scales
![]() $L/\unicode[STIX]{x1D6FF}_{o}\gtrsim 4$
(Clemens & Narayanaswamy Reference Clemens and Narayanaswamy2014). As further noted in the scaling analysis by Souverein, Bakker & Dupont (Reference Souverein, Bakker and Dupont2013), cases to have reported a strong downstream influence generally involve relatively low Reynolds numbers, in part linked to separation scale too. It however remains unclear how strong an impact these different factors may bear on the low-frequency unsteadiness and to what extent their influence may vary amongst cases.
$L/\unicode[STIX]{x1D6FF}_{o}\gtrsim 4$
(Clemens & Narayanaswamy Reference Clemens and Narayanaswamy2014). As further noted in the scaling analysis by Souverein, Bakker & Dupont (Reference Souverein, Bakker and Dupont2013), cases to have reported a strong downstream influence generally involve relatively low Reynolds numbers, in part linked to separation scale too. It however remains unclear how strong an impact these different factors may bear on the low-frequency unsteadiness and to what extent their influence may vary amongst cases.
The present research follows from our recent experimental studies on a highly separated axisymmetric Mach 3.9 STBLI, at high Reynolds number
![]() $Re_{e}=6.1\times 10^{7}~\text{m}^{-1}$
(
$Re_{e}=6.1\times 10^{7}~\text{m}^{-1}$
(
![]() $Re_{\unicode[STIX]{x1D6FF}}=2.3\times 10^{5}$
), where we looked at the unsteady nature of a step-induced separation of length
$Re_{\unicode[STIX]{x1D6FF}}=2.3\times 10^{5}$
), where we looked at the unsteady nature of a step-induced separation of length
![]() ${\sim}30\unicode[STIX]{x1D6FF}_{o}$
upstream of the step and extending
${\sim}30\unicode[STIX]{x1D6FF}_{o}$
upstream of the step and extending
![]() ${\sim}10\unicode[STIX]{x1D6FF}_{o}$
behind it (Chandola, Huang & Estruch-Samper Reference Chandola, Huang and Estruch-Samper2017). The characteristic flow organisation may be seen in the schlieren image in figure 1. The boundary layer first separates at
${\sim}10\unicode[STIX]{x1D6FF}_{o}$
behind it (Chandola, Huang & Estruch-Samper Reference Chandola, Huang and Estruch-Samper2017). The characteristic flow organisation may be seen in the schlieren image in figure 1. The boundary layer first separates at
![]() $S_{1}$
well upstream of the step – of height
$S_{1}$
well upstream of the step – of height
![]() $h=22.5~\text{mm}$
(
$h=22.5~\text{mm}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
) – and reattaches at its upper edge
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
) – and reattaches at its upper edge
![]() $R_{1}$
, leading to the formation of an upstream oblique shock with origin near separation and a detached reattachment shock close ahead of the step, given the high deflection experienced by the reattaching flow. Downstream of the step, a second separation region develops between its trailing edge
$R_{1}$
, leading to the formation of an upstream oblique shock with origin near separation and a detached reattachment shock close ahead of the step, given the high deflection experienced by the reattaching flow. Downstream of the step, a second separation region develops between its trailing edge
![]() $S_{2}$
and downstream reattachment at the wall
$S_{2}$
and downstream reattachment at the wall
![]() $R_{2}$
(base cylinder), where a weaker shock is induced. Also indicated in the image are the normalised locations
$R_{2}$
(base cylinder), where a weaker shock is induced. Also indicated in the image are the normalised locations
![]() $X^{\ast }=X/L$
, where
$X^{\ast }=X/L$
, where
![]() $X=x-x_{o}$
is the distance from the respective mean separation locations: with
$X=x-x_{o}$
is the distance from the respective mean separation locations: with
![]() $X_{U}^{\ast }=0$
and 1 referring to the upstream region (
$X_{U}^{\ast }=0$
and 1 referring to the upstream region (
![]() $S_{1},R_{1}$
) and
$S_{1},R_{1}$
) and
![]() $X_{D}^{\ast }=0$
and 1 to that behind the step (
$X_{D}^{\ast }=0$
and 1 to that behind the step (
![]() $S_{2}$
,
$S_{2}$
,
![]() $R_{2}$
). Despite early tests initially contemplating the possibility of a prevalent influence of upstream superstructures, results led us to shift our focus to the shear layer arising between the inner separation region and the outer high-speed flow – as clearly evidenced in the schlieren as well.
$R_{2}$
). Despite early tests initially contemplating the possibility of a prevalent influence of upstream superstructures, results led us to shift our focus to the shear layer arising between the inner separation region and the outer high-speed flow – as clearly evidenced in the schlieren as well.
Having noted the above, we thus set off to characterise the shear layer’s influence on interaction unsteadiness as the separation scale is varied by over an order of magnitude in § 3. Subsequently, in order to further evaluate the role of the shear layer at different flow conditions, the effects of Mach number and Reynolds number are investigated in § 4. Before proceeding with the results, details on the experimental procedures are first given in the following section.
2 Methodology
2.1 Experimental programme
Experiments were conducted in a high-speed intermittent blowdown wind tunnel with a 1.22 m
![]() $\times$
1.22 m test section (4 ft
$\times$
1.22 m test section (4 ft
![]() $\times$
4 ft) and using air as the test gas (the ‘trisonic’ Singapore National Wind Tunnel Facility). The test model consists of a stainless steel ogive cylinder body with a base cylinder diameter of
$\times$
4 ft) and using air as the test gas (the ‘trisonic’ Singapore National Wind Tunnel Facility). The test model consists of a stainless steel ogive cylinder body with a base cylinder diameter of
![]() $D_{B}=75~\text{mm}$
, nose radius
$D_{B}=75~\text{mm}$
, nose radius
![]() $R_{N}=655.7~\text{mm}$
and length
$R_{N}=655.7~\text{mm}$
and length
![]() $L_{N}=218.6~\text{mm}$
(
$L_{N}=218.6~\text{mm}$
(
![]() $1/3R_{N}$
), aligned at zero incidence to the free stream. The complete test model dimensions are indicated in the schematic in figure 2, where the geometry is shown parametrised as a function of base cylinder diameter
$1/3R_{N}$
), aligned at zero incidence to the free stream. The complete test model dimensions are indicated in the schematic in figure 2, where the geometry is shown parametrised as a function of base cylinder diameter
![]() $D_{B}$
. The model has a total length of 0.9 m (
$D_{B}$
. The model has a total length of 0.9 m (
![]() $12D_{B}$
) from the nose to the beginning of sting mount and is comprised of a number of modules, with instrumentation fitted within the base cylindrical body and model surface highly polished as an ensemble. Axisymmetric step height is changed between tests by replacing a disk of diameter
$12D_{B}$
) from the nose to the beginning of sting mount and is comprised of a number of modules, with instrumentation fitted within the base cylindrical body and model surface highly polished as an ensemble. Axisymmetric step height is changed between tests by replacing a disk of diameter
![]() $D_{S}$
which is located over the cylindrical section of the body at
$D_{S}$
which is located over the cylindrical section of the body at
![]() $x_{S}=450~\text{mm}$
(
$x_{S}=450~\text{mm}$
(
![]() $6D_{B}$
) from the nose leading edge, with modules routinely detached at the step location only. Measurements were taken over the cylindrical surface on the two sides of the step to document both the upstream forward-facing step (FFS) and downstream backward-facing step (BFS) regions. The results for both regions are presented in the following section to assess the overall dynamics of the supersonic step flow (including downstream influence). The low-frequency unsteadiness analysis thereafter centres on the axisymmetric FFS as a canonical configuration with fully undisturbed (reference) incoming conditions.
$6D_{B}$
) from the nose leading edge, with modules routinely detached at the step location only. Measurements were taken over the cylindrical surface on the two sides of the step to document both the upstream forward-facing step (FFS) and downstream backward-facing step (BFS) regions. The results for both regions are presented in the following section to assess the overall dynamics of the supersonic step flow (including downstream influence). The low-frequency unsteadiness analysis thereafter centres on the axisymmetric FFS as a canonical configuration with fully undisturbed (reference) incoming conditions.

Figure 2. Test model diagram with dimensions parametrised as a function of base cylinder diameter
![]() $D_{B}$
: ogive nose length (
$D_{B}$
: ogive nose length (
![]() $3D_{B}$
), upstream cylinder section (
$3D_{B}$
), upstream cylinder section (
![]() $3D_{B}$
), downstream cylinder section (
$3D_{B}$
), downstream cylinder section (
![]() $4.35D_{B}$
) and sting mount adaptor (
$4.35D_{B}$
) and sting mount adaptor (
![]() $4.6D_{B}$
).
$4.6D_{B}$
).
![]() $R_{N}$
and
$R_{N}$
and
![]() $D_{S}$
are nose radius and axisymmetric step (
$D_{S}$
are nose radius and axisymmetric step (
![]() $90^{\circ }$
-disk) diameter. Length from step leading to trailing edge is
$90^{\circ }$
-disk) diameter. Length from step leading to trailing edge is
![]() $l_{S}=0.3D_{B}$
and height
$l_{S}=0.3D_{B}$
and height
![]() $h=(D_{S}-D_{B})/2$
, where
$h=(D_{S}-D_{B})/2$
, where
![]() $D_{B}=75~\text{mm}$
. Sting mount starts 0.45 m (
$D_{B}=75~\text{mm}$
. Sting mount starts 0.45 m (
![]() $6D_{B}$
) from step leading edge. Model at
$6D_{B}$
) from step leading edge. Model at
![]() $0^{\circ }$
-incidence and centred within 1.22 m
$0^{\circ }$
-incidence and centred within 1.22 m
![]() $\times$
1.22 m (4 ft
$\times$
1.22 m (4 ft
![]() $\times$
4 ft) test section.
$\times$
4 ft) test section.
The scaling of the mean separation bubble poses a number of experimental challenges, with features such as recirculation height often proving difficult to estimate (Souverein et al.
Reference Souverein, Bakker and Dupont2013). The choice for an axisymmetric FFS here aimed at producing a well-defined and scalable recirculation region, with bubble height effectively altered through step height
![]() $h$
variations and separation length
$h$
variations and separation length
![]() $L$
accurately identifiable from the results, thus enabling a systematic investigation with sensible estimates of the mean flow organisation and mass in the bubble
$L$
accurately identifiable from the results, thus enabling a systematic investigation with sensible estimates of the mean flow organisation and mass in the bubble
![]() $M_{B}$
(§ 5). A total of 15 disks with a diameter range of
$M_{B}$
(§ 5). A total of 15 disks with a diameter range of
![]() $D_{S}=78$
–120 mm were used to alter the interaction scale, yielding
$D_{S}=78$
–120 mm were used to alter the interaction scale, yielding
![]() $\unicode[STIX]{x0394}h=1.5~\text{mm}$
variations between the shortest
$\unicode[STIX]{x0394}h=1.5~\text{mm}$
variations between the shortest
![]() $h=1.5~\text{mm}$
step and up to
$h=1.5~\text{mm}$
step and up to
![]() $h=22.5~\text{mm}$
, where axisymmetric step height is
$h=22.5~\text{mm}$
, where axisymmetric step height is
![]() $h=(D_{S}-D_{B})/2$
. The tallest step corresponds to the highly separated interaction in figure 1 (
$h=(D_{S}-D_{B})/2$
. The tallest step corresponds to the highly separated interaction in figure 1 (
![]() $h=22.5~\text{mm}$
, at Mach 3.9), which serves as a reference across the study. Test model cross-sectional area for this larger configuration is 0.8 % of the tunnel test section and the step length-to-height ratio for the same is
$h=22.5~\text{mm}$
, at Mach 3.9), which serves as a reference across the study. Test model cross-sectional area for this larger configuration is 0.8 % of the tunnel test section and the step length-to-height ratio for the same is
![]() $l_{S}/h=1$
, with
$l_{S}/h=1$
, with
![]() $l_{S}=22.5~\text{mm}$
kept constant for all cases. As established for the reference case, a reduction in step length down to
$l_{S}=22.5~\text{mm}$
kept constant for all cases. As established for the reference case, a reduction in step length down to
![]() $1/3l_{S}$
bears no influence on the upstream separation, i.e. reattachment
$1/3l_{S}$
bears no influence on the upstream separation, i.e. reattachment
![]() $R_{1}$
effectively takes place at step leading edge (upper lip) for all the interactions considered here,
$R_{1}$
effectively takes place at step leading edge (upper lip) for all the interactions considered here,
![]() $l_{S}/h\geqslant 1$
.
$l_{S}/h\geqslant 1$
.
Figure 3 presents the total pressure
![]() $P_{o,\infty }$
and temperature
$P_{o,\infty }$
and temperature
![]() $T_{o,\infty }$
traces for the different free-stream Mach numbers considered in the experiments:
$T_{o,\infty }$
traces for the different free-stream Mach numbers considered in the experiments:
![]() $M_{\infty }=3.93$
, 2.95 and 1.97. The conditions shown here were selected at a common free-stream Reynolds number of
$M_{\infty }=3.93$
, 2.95 and 1.97. The conditions shown here were selected at a common free-stream Reynolds number of
![]() $Re_{\infty }/m=70.1\times 10^{6}$
, as achieved with total pressures accordingly of
$Re_{\infty }/m=70.1\times 10^{6}$
, as achieved with total pressures accordingly of
![]() $P_{o,\infty }=1543$
kPa, 915 kPa and 553 kPa, from higher to lower Mach number and within
$P_{o,\infty }=1543$
kPa, 915 kPa and 553 kPa, from higher to lower Mach number and within
![]() $\pm 0.2$
%–0.7 % uncertainty. The total temperatures for the same cases were
$\pm 0.2$
%–0.7 % uncertainty. The total temperatures for the same cases were
![]() $T_{o,\infty }=308~\text{K}$
, 303 K and 302 K (
$T_{o,\infty }=308~\text{K}$
, 303 K and 302 K (
![]() $\pm 1.5\,\%$
); wall temperature is adiabatic at
$\pm 1.5\,\%$
); wall temperature is adiabatic at
![]() $T_{w}\approx 284~\text{K}$
for the reference undisturbed flow at
$T_{w}\approx 284~\text{K}$
for the reference undisturbed flow at
![]() $M_{\infty }=3.93$
;
$M_{\infty }=3.93$
;
![]() $T_{w}\approx 282~\text{K}$
at
$T_{w}\approx 282~\text{K}$
at
![]() $M_{\infty }=2.95$
and
$M_{\infty }=2.95$
and
![]() $M_{\infty }=1.97$
. The measurement windows were taken respectively at 15 s, 8.5 s and 6 s from tunnel start (from higher to lower
$M_{\infty }=1.97$
. The measurement windows were taken respectively at 15 s, 8.5 s and 6 s from tunnel start (from higher to lower
![]() $M_{\infty }$
) with a duration of 5.24 s for all cases. The highest Mach number condition is the same as that for the reference highly separated case and serves for the investigation of the interaction scale effect (§ 3). The other two conditions are then used to study the effect of Mach number, with two further cases later used where Reynolds number is varied as well (§ 4).
$M_{\infty }$
) with a duration of 5.24 s for all cases. The highest Mach number condition is the same as that for the reference highly separated case and serves for the investigation of the interaction scale effect (§ 3). The other two conditions are then used to study the effect of Mach number, with two further cases later used where Reynolds number is varied as well (§ 4).
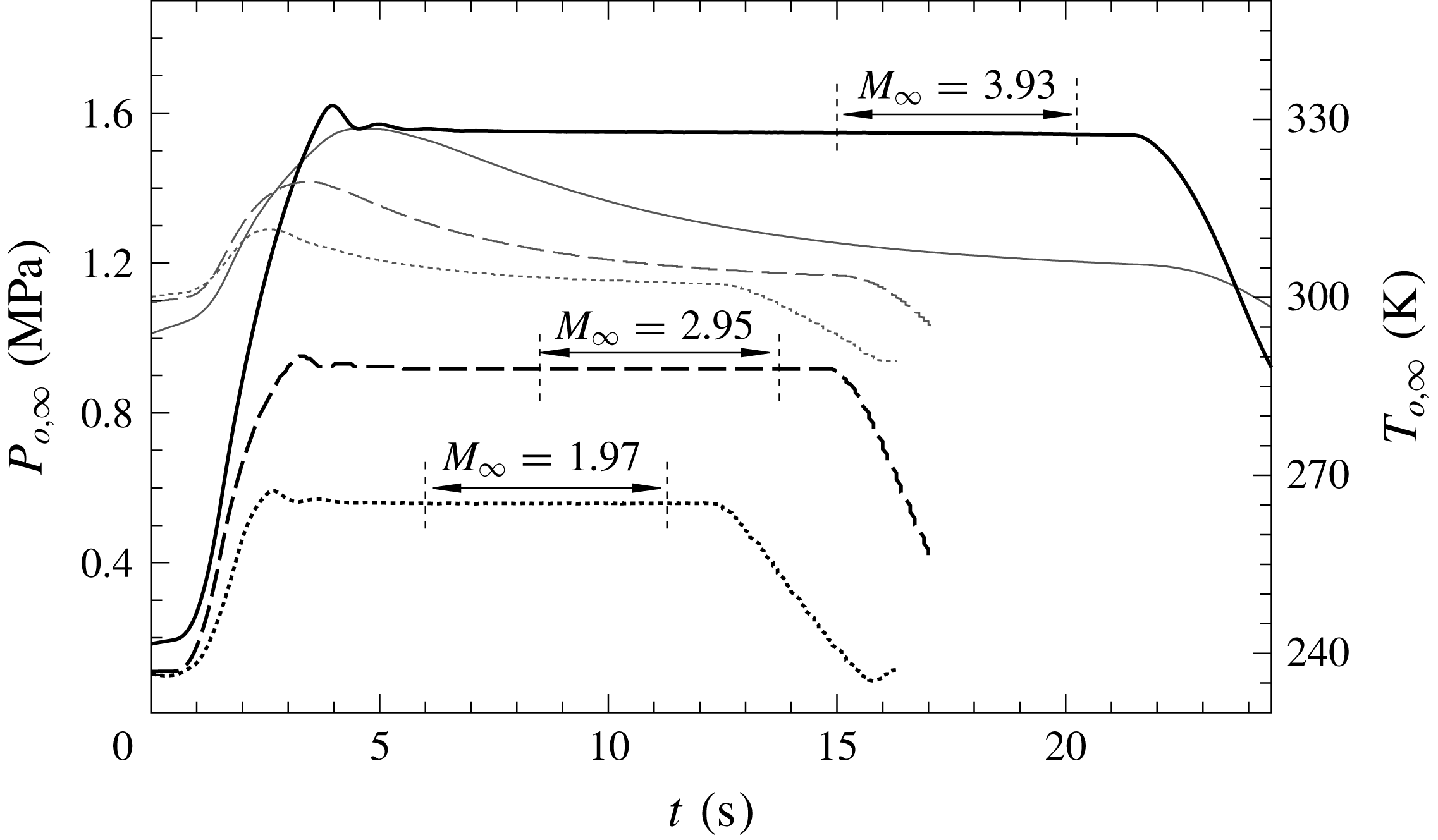
Figure 3. Free-stream total pressure
![]() $P_{o,\infty }$
(black lines, left axis) and total temperature
$P_{o,\infty }$
(black lines, left axis) and total temperature
![]() $T_{o,\infty }$
(grey lines, right axis) at
$T_{o,\infty }$
(grey lines, right axis) at
![]() $M_{\infty }=3.93$
,
$M_{\infty }=3.93$
,
![]() $Re_{\infty }=70.1\times 10^{6}~\text{m}^{-1}$
(solid lines),
$Re_{\infty }=70.1\times 10^{6}~\text{m}^{-1}$
(solid lines),
![]() $M_{\infty }=2.95$
,
$M_{\infty }=2.95$
,
![]() $Re_{\infty }=70.1\times 10^{6}~\text{m}^{-1}$
(long dashed lines) and
$Re_{\infty }=70.1\times 10^{6}~\text{m}^{-1}$
(long dashed lines) and
![]() $M_{\infty }=1.97$
,
$M_{\infty }=1.97$
,
![]() $Re_{\infty }=70.1\times 10^{6}~\text{m}^{-1}$
(short dashed lines). Test window is taken respectively at 15–20.24 s, 8.5–13.74 s and 6–11.24 s as indicated over the
$Re_{\infty }=70.1\times 10^{6}~\text{m}^{-1}$
(short dashed lines). Test window is taken respectively at 15–20.24 s, 8.5–13.74 s and 6–11.24 s as indicated over the
![]() $P_{o,\infty }$
traces (kept with a common duration of 5.24 s for unsteadiness analysis).
$P_{o,\infty }$
traces (kept with a common duration of 5.24 s for unsteadiness analysis).
2.2 Undisturbed axisymmetric boundary layer
The reference flow conditions were characterised during the experimental design stages of the study using computational fluid dynamics (CFD) with the aim of establishing a simplified base geometry, common across tests, and with minimal flow gradients over the measurement region. Simulations modelled the complete ogive cylinder body, without a step, using a Reynolds-averaged Navier–Stokes (RANS) numerical procedure with the algebraic turbulence model of Baldwin & Lomax (Reference Baldwin and Lomax1978), using a similar approach as in the axisymmetric STBLI studies by Murray, Hillier & Williams (Reference Murray, Hillier and Williams2013). For all cases, three mesh levels were considered, each with successive halving of cell dimensions (structured, with quadrilateral cells and adapted to trace the flow close upstream of the nose leading edge shock); the results presented in figure 4(a–c) correspond to both the coarsest and the finest meshes in the study, with grid details as specified in the figure caption. Following the compression and expansion effects over the nose and nose/cylinder junction, the surface flow conditions over the cylindrical section are then seen to become established, with the edge Mach number along the measurement region upstream of the step decreasing slightly by under
![]() $\unicode[STIX]{x0394}M_{e}<0.9\,\%$
,
$\unicode[STIX]{x0394}M_{e}<0.9\,\%$
,
![]() ${<}1.0\,\%$
and
${<}1.0\,\%$
and
![]() ${<}1.1\,\%$
from higher to lower
${<}1.1\,\%$
from higher to lower
![]() $M_{\infty }$
(over
$M_{\infty }$
(over
![]() $-1.92D_{B}<x<x_{S}$
, as concerned in the low-frequency analysis, § 5). Edge Reynolds number instead increases by
$-1.92D_{B}<x<x_{S}$
, as concerned in the low-frequency analysis, § 5). Edge Reynolds number instead increases by
![]() $\unicode[STIX]{x0394}Re_{e}<1.6\,\%$
,
$\unicode[STIX]{x0394}Re_{e}<1.6\,\%$
,
![]() ${<}1.5\,\%$
and
${<}1.5\,\%$
and
![]() ${<}0.8\,\%$
accordingly, with pressure following a similar tendency.
${<}0.8\,\%$
accordingly, with pressure following a similar tendency.

Figure 4. Reference pressure
![]() $p$
(solid lines, left axis), edge Mach number
$p$
(solid lines, left axis), edge Mach number
![]() $M_{e}$
(short dashed lines, right axis) and Reynolds number
$M_{e}$
(short dashed lines, right axis) and Reynolds number
![]() $Re_{e}$
(long dashed lines, right axis) for: (a)
$Re_{e}$
(long dashed lines, right axis) for: (a)
![]() $M_{\infty }=3.93$
,
$M_{\infty }=3.93$
,
![]() $Re_{\infty }=7.0\times 10^{7}~\text{m}^{-1}$
, (b)
$Re_{\infty }=7.0\times 10^{7}~\text{m}^{-1}$
, (b)
![]() $M_{\infty }=2.95$
,
$M_{\infty }=2.95$
,
![]() $Re_{\infty }=7.0\times 10^{7}~\text{m}^{-1}$
and (c)
$Re_{\infty }=7.0\times 10^{7}~\text{m}^{-1}$
and (c)
![]() $M_{\infty }=1.97$
,
$M_{\infty }=1.97$
,
![]() $Re_{\infty }=7.0\times 10^{7}~\text{m}^{-1}$
. Based on turbulent CFD (
$Re_{\infty }=7.0\times 10^{7}~\text{m}^{-1}$
. Based on turbulent CFD (
![]() $N_{x}\times N_{y}=1301\times 1500$
,
$N_{x}\times N_{y}=1301\times 1500$
,
![]() $y^{+}=1$
for fine resolution mesh in black;
$y^{+}=1$
for fine resolution mesh in black;
![]() $N_{x}\times N_{y}=323\times 374$
,
$N_{x}\times N_{y}=323\times 374$
,
![]() $y^{+}=4$
for coarse mesh in grey). Medium case (
$y^{+}=4$
for coarse mesh in grey). Medium case (
![]() $N_{x}\times N_{y}=647\times 747$
,
$N_{x}\times N_{y}=647\times 747$
,
![]() $y^{+}=2$
) not shown for illustration purposes. Grey square marks step location during the experiments (typical CFD domain schematic as shown on the top, with mesh fitted to ogive nose leading edge shock wave for each case).
$y^{+}=2$
) not shown for illustration purposes. Grey square marks step location during the experiments (typical CFD domain schematic as shown on the top, with mesh fitted to ogive nose leading edge shock wave for each case).
![]() $p_{\infty }=11.16$
kPa, 26.85 kPa and 74.05 kPa from higher to lower Mach number.
$p_{\infty }=11.16$
kPa, 26.85 kPa and 74.05 kPa from higher to lower Mach number.

Figure 5. Incoming boundary-layer profiles: (a) velocity
![]() $u$
and (b) Mach number
$u$
and (b) Mach number
![]() $M$
, (c) close up to log-law region and comparison with past studies and (d) spectra based on wall measurements
$M$
, (c) close up to log-law region and comparison with past studies and (d) spectra based on wall measurements
![]() $y=0$
and ‘high-frequency Pitot’ measurements with probe head at
$y=0$
and ‘high-frequency Pitot’ measurements with probe head at
![]() $y\approx (0.7\pm 0.2)\unicode[STIX]{x1D6FF}_{o}$
. Experimental measurements in panels (a–c) taken with miniature probe in
$y\approx (0.7\pm 0.2)\unicode[STIX]{x1D6FF}_{o}$
. Experimental measurements in panels (a–c) taken with miniature probe in
![]() $\unicode[STIX]{x0394}y=0.2~\text{mm}$
steps (symbols) and numerical predictions indicated with lines as:
$\unicode[STIX]{x0394}y=0.2~\text{mm}$
steps (symbols) and numerical predictions indicated with lines as:
![]() $M_{\infty }=3.93$
(solid line),
$M_{\infty }=3.93$
(solid line),
![]() $M_{\infty }=2.95$
(long dashed line) and
$M_{\infty }=2.95$
(long dashed line) and
![]() $M_{\infty }=1.97$
(short dashed line); with reference one-seventh power-law velocity profiles in grey
$M_{\infty }=1.97$
(short dashed line); with reference one-seventh power-law velocity profiles in grey
![]() $u/U_{e}=(y/\unicode[STIX]{x1D6FF}_{o})^{1/7}$
. Respective
$u/U_{e}=(y/\unicode[STIX]{x1D6FF}_{o})^{1/7}$
. Respective
![]() $\unicode[STIX]{x1D6FF}_{3.9}$
,
$\unicode[STIX]{x1D6FF}_{3.9}$
,
![]() $\unicode[STIX]{x1D6FF}_{3.0}$
and
$\unicode[STIX]{x1D6FF}_{3.0}$
and
![]() $\unicode[STIX]{x1D6FF}_{2.0}$
levels indicate local boundary-layer thickness taken at
$\unicode[STIX]{x1D6FF}_{2.0}$
levels indicate local boundary-layer thickness taken at
![]() $y=99.5\,\%U_{e}$
. Lines in panel (d) correspond to
$y=99.5\,\%U_{e}$
. Lines in panel (d) correspond to
![]() $M_{\infty }=3.93$
(black),
$M_{\infty }=3.93$
(black),
![]() $M_{\infty }=2.95$
(dark grey) and
$M_{\infty }=2.95$
(dark grey) and
![]() $M_{\infty }=1.97$
(light grey) cases, with grey area indicating region outside sensor range (
$M_{\infty }=1.97$
(light grey) cases, with grey area indicating region outside sensor range (
![]() ${>}50~\text{kHz}$
). All measurements taken at
${>}50~\text{kHz}$
). All measurements taken at
![]() $x=336~\text{mm}$
on base model without the step, as per table 1.
$x=336~\text{mm}$
on base model without the step, as per table 1.
The undisturbed boundary-layer profiles were measured using an in-house Pitot tube, probing the near-wall flow in
![]() $\unicode[STIX]{x0394}y=0.2~\text{mm}$
steps (
$\unicode[STIX]{x0394}y=0.2~\text{mm}$
steps (
![]() $\pm 1.3\,\%$
). As a common reference, measurements were obtained at the
$\pm 1.3\,\%$
). As a common reference, measurements were obtained at the
![]() $S_{1}$
location for the reference highly separated test case (
$S_{1}$
location for the reference highly separated test case (
![]() $h=22.5~\text{mm}$
,
$h=22.5~\text{mm}$
,
![]() $M_{e}=3.9$
), corresponding to
$M_{e}=3.9$
), corresponding to
![]() $x=336~\text{mm}$
(
$x=336~\text{mm}$
(
![]() $x_{S}$
–
$x_{S}$
–
![]() $30\unicode[STIX]{x1D6FF}_{o}$
) from the nose leading edge, and without a step on the model (base body only). As shown in figure 5, both the CFD estimates and experimental measurements follow closely a power-law velocity profile,
$30\unicode[STIX]{x1D6FF}_{o}$
) from the nose leading edge, and without a step on the model (base body only). As shown in figure 5, both the CFD estimates and experimental measurements follow closely a power-law velocity profile,
![]() $u/U_{e}=(y/\unicode[STIX]{x1D6FF}_{o})^{1/n}$
, precisely with
$u/U_{e}=(y/\unicode[STIX]{x1D6FF}_{o})^{1/n}$
, precisely with
![]() $n=6.5\pm 0.5$
, and the Mach number trends are also as expected for a high Mach number turbulent boundary layer, with the growth downstream of the measurement location being thereafter estimated from theory/CFD. For the highly separated cases, the reference boundary-layer thickness with the edge taken at
$n=6.5\pm 0.5$
, and the Mach number trends are also as expected for a high Mach number turbulent boundary layer, with the growth downstream of the measurement location being thereafter estimated from theory/CFD. For the highly separated cases, the reference boundary-layer thickness with the edge taken at
![]() $99.5\,\%U_{e}$
is respectively
$99.5\,\%U_{e}$
is respectively
![]() $\unicode[STIX]{x1D6FF}_{o}=3.8~\text{mm}$
(for
$\unicode[STIX]{x1D6FF}_{o}=3.8~\text{mm}$
(for
![]() $M_{e}=3.9$
),
$M_{e}=3.9$
),
![]() $\unicode[STIX]{x1D6FF}_{o}=3.2~\text{mm}$
(
$\unicode[STIX]{x1D6FF}_{o}=3.2~\text{mm}$
(
![]() $M_{e}=3.0$
) and
$M_{e}=3.0$
) and
![]() $\unicode[STIX]{x1D6FF}_{o}=2.8~\text{mm}$
(
$\unicode[STIX]{x1D6FF}_{o}=2.8~\text{mm}$
(
![]() $M_{e}=2.0$
). Further reference conditions, including temperature and velocity at the boundary-layer edge
$M_{e}=2.0$
). Further reference conditions, including temperature and velocity at the boundary-layer edge
![]() $T_{e}$
and
$T_{e}$
and
![]() $U_{e}$
, are given in table 1.
$U_{e}$
, are given in table 1.
Table 1. Nominal flow conditions: free-stream Mach number
![]() $M_{\infty }$
and total pressure
$M_{\infty }$
and total pressure
![]() $P_{o,\infty }$
; edge Mach number
$P_{o,\infty }$
; edge Mach number
![]() $M_{e}$
, static temperature
$M_{e}$
, static temperature
![]() $T_{e}$
, velocity
$T_{e}$
, velocity
![]() $U_{e}$
, unit Reynolds number
$U_{e}$
, unit Reynolds number
![]() $Re_{e}/m$
and boundary-layer thickness
$Re_{e}/m$
and boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{o}$
. Reference conditions taken at
$\unicode[STIX]{x1D6FF}_{o}$
. Reference conditions taken at
![]() $S_{1}$
(
$S_{1}$
(
![]() $X_{U}^{\ast }=0$
) for Mach 3.9
$X_{U}^{\ast }=0$
) for Mach 3.9
![]() $h=22.5$
mm case (reference highly separated STBLI), i.e. at
$h=22.5$
mm case (reference highly separated STBLI), i.e. at
![]() $x=336~\text{mm}$
on the ogive cylinder body without the step.
$x=336~\text{mm}$
on the ogive cylinder body without the step.

Comparison with the velocity profiles documented for other high-speed turbulent boundary layers – at Mach 2.3 in the experiments by Dupont et al. (Reference Dupont, Haddad and Debiève2006) and Mach 5.8 in the DNS by Duan, Choudhari & Zhang (Reference Duan, Choudhari and Zhang2016) – finds the reference flow to comply with the expected linear trend in the log-law region, with a similar tendency across the
![]() $M_{e}=2.0$
–3.9 range. For all cases, and consistently with the trends noted in the latter DNS studies, as well as in other high-speed turbulent boundary-layer assessments (e.g. see Beresh et al.
Reference Beresh, Henfling, Spillers and Pruett2011), the wall-pressure spectrum for the undisturbed boundary layer remains broadband at the lower-frequency range (
$M_{e}=2.0$
–3.9 range. For all cases, and consistently with the trends noted in the latter DNS studies, as well as in other high-speed turbulent boundary-layer assessments (e.g. see Beresh et al.
Reference Beresh, Henfling, Spillers and Pruett2011), the wall-pressure spectrum for the undisturbed boundary layer remains broadband at the lower-frequency range (
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
, where
$\unicode[STIX]{x1D714}\rightarrow 0$
, where
![]() $\unicode[STIX]{x1D714}$
is angular frequency) and then exhibits a
$\unicode[STIX]{x1D714}$
is angular frequency) and then exhibits a
![]() $\unicode[STIX]{x1D714}^{-1}$
dependence at higher frequencies. Measurements subsequently taken within the log-law region, with an in-house ‘high-frequency Pitot tube’ using a fast-response piezoresistive silicon pressure transducer (Kulite XCQ-055), find the onset for the latter trend delayed to higher frequencies; this is consistent with the
$\unicode[STIX]{x1D714}^{-1}$
dependence at higher frequencies. Measurements subsequently taken within the log-law region, with an in-house ‘high-frequency Pitot tube’ using a fast-response piezoresistive silicon pressure transducer (Kulite XCQ-055), find the onset for the latter trend delayed to higher frequencies; this is consistent with the
![]() $\unicode[STIX]{x1D714}^{-1}$
tendency at mid-frequencies being attributed to the acoustic influence of eddies in the logarithmic region and with length scale proportional to distance from the wall (Bradshaw Reference Bradshaw1967). At frequencies above the documented range (
$\unicode[STIX]{x1D714}^{-1}$
tendency at mid-frequencies being attributed to the acoustic influence of eddies in the logarithmic region and with length scale proportional to distance from the wall (Bradshaw Reference Bradshaw1967). At frequencies above the documented range (
![]() ${\gtrsim}50~\text{kHz}$
), the spectra would then be expected to switch to a
${\gtrsim}50~\text{kHz}$
), the spectra would then be expected to switch to a
![]() $\unicode[STIX]{x1D714}^{-7/3}$
tendency, followed by
$\unicode[STIX]{x1D714}^{-7/3}$
tendency, followed by
![]() $\unicode[STIX]{x1D714}^{-5}$
, up to a dominant frequency of order
$\unicode[STIX]{x1D714}^{-5}$
, up to a dominant frequency of order
![]() ${\sim}U_{e}/\unicode[STIX]{x1D6FF}_{o}$
(
${\sim}U_{e}/\unicode[STIX]{x1D6FF}_{o}$
(
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}_{o}/U_{e}\approx 2\unicode[STIX]{x03C0}$
) at the characteristic frequency of the energetic vortical structures within the boundary layer (e.g. see Smits & Dussauge Reference Smits and Dussauge2006b
). Overall, the incoming boundary layer is established to be at equilibrium upstream of the interaction and naturally developed to a fully turbulent state for the conditions hereby considered.
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}_{o}/U_{e}\approx 2\unicode[STIX]{x03C0}$
) at the characteristic frequency of the energetic vortical structures within the boundary layer (e.g. see Smits & Dussauge Reference Smits and Dussauge2006b
). Overall, the incoming boundary layer is established to be at equilibrium upstream of the interaction and naturally developed to a fully turbulent state for the conditions hereby considered.
2.3 Wall-pressure measurements
The immediate impact of STBLI unsteadiness on surface pressure renders this property both a relevant and sensitive measure for the present purposes. The fast-response piezoresistive silicon pressure transducers used for the study (Kulite XCQ-055, rated at 25 psi absolute and
![]() $f_{n}=210~\text{kHz}$
natural frequency) were selected for their high spatial resolution and frequency response; they use a Kulite ‘b-screen’ composed of eight 0.15 mm-diameter tappings in a circular arrangement of diameter
$f_{n}=210~\text{kHz}$
natural frequency) were selected for their high spatial resolution and frequency response; they use a Kulite ‘b-screen’ composed of eight 0.15 mm-diameter tappings in a circular arrangement of diameter
![]() $d_{\unicode[STIX]{x1D705},1}=0.87~\text{mm}$
and with sensor outer diameter
$d_{\unicode[STIX]{x1D705},1}=0.87~\text{mm}$
and with sensor outer diameter
![]() $d_{\unicode[STIX]{x1D705},2}=1.40~\text{mm}$
. The high elastic modulus of the silicon diaphragm, combined with its small mass and high stiffness, is designed to yield a flat frequency response (
$d_{\unicode[STIX]{x1D705},2}=1.40~\text{mm}$
. The high elastic modulus of the silicon diaphragm, combined with its small mass and high stiffness, is designed to yield a flat frequency response (
![]() $0\pm 2$
dB) up to
$0\pm 2$
dB) up to
![]() ${\sim}0.2f_{n}$
, with gain progressively enhanced towards
${\sim}0.2f_{n}$
, with gain progressively enhanced towards
![]() $f_{n}$
, with approximately
$f_{n}$
, with approximately
![]() $+3$
dB by 50 kHz. Based on assessments on the more widely validated XCQ-062 type transducers (e.g. Hurst et al.
Reference Hurst, Olsen, Goodman, Vandeweert and Shang2014), and noting the cavity volume is nearly halved in this latest design, the resonance frequency is safely estimated at the upper end of the range, with no evidence of a signature noted within 0–50 kHz in the results – e.g. as established from the practically flat spectral levels prior to shear layer inception – and with a steep roll-off thereafter (55–70 kHz). Spatial resolution in terms of
$+3$
dB by 50 kHz. Based on assessments on the more widely validated XCQ-062 type transducers (e.g. Hurst et al.
Reference Hurst, Olsen, Goodman, Vandeweert and Shang2014), and noting the cavity volume is nearly halved in this latest design, the resonance frequency is safely estimated at the upper end of the range, with no evidence of a signature noted within 0–50 kHz in the results – e.g. as established from the practically flat spectral levels prior to shear layer inception – and with a steep roll-off thereafter (55–70 kHz). Spatial resolution in terms of
![]() $\unicode[STIX]{x1D714}d_{\unicode[STIX]{x1D705},2}/2U_{c}$
, where
$\unicode[STIX]{x1D714}d_{\unicode[STIX]{x1D705},2}/2U_{c}$
, where
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $U_{c}$
are angular frequency and convection velocity, suggests minimal attenuation of energy scales much smaller than the sensor size, with the
$U_{c}$
are angular frequency and convection velocity, suggests minimal attenuation of energy scales much smaller than the sensor size, with the
![]() $-3$
dB point (at
$-3$
dB point (at
![]() $\unicode[STIX]{x1D714}d_{\unicode[STIX]{x1D705},2}/2U_{c}=1$
, as per Corcos Reference Corcos1963) well above the 50 kHz threshold considered here.
$\unicode[STIX]{x1D714}d_{\unicode[STIX]{x1D705},2}/2U_{c}=1$
, as per Corcos Reference Corcos1963) well above the 50 kHz threshold considered here.
For each test, the output of 32 sensors was simultaneously acquired at a sampling rate of
![]() $200~\text{kS}~\text{s}^{-1}$
per channel at 24-bit (DeweSoft SIRIUSi system), with a cutoff at 100 kHz prior to digitisation. Sensors were flush mounted on the model surface and spaced at
$200~\text{kS}~\text{s}^{-1}$
per channel at 24-bit (DeweSoft SIRIUSi system), with a cutoff at 100 kHz prior to digitisation. Sensors were flush mounted on the model surface and spaced at
![]() $\unicode[STIX]{x1D709}=4.5~\text{mm}$
, axially aligned starting 2.25 mm from the step (
$\unicode[STIX]{x1D709}=4.5~\text{mm}$
, axially aligned starting 2.25 mm from the step (
![]() $\unicode[STIX]{x1D709}=9~\text{mm}$
for simultaneous FFS/BFS measurements). Unsteady data analysis considers test windows with a duration of 5.24 s in all cases and spectral quantities are obtained by ensemble averaging 64 segments of
$\unicode[STIX]{x1D709}=9~\text{mm}$
for simultaneous FFS/BFS measurements). Unsteady data analysis considers test windows with a duration of 5.24 s in all cases and spectral quantities are obtained by ensemble averaging 64 segments of
![]() $2^{14}$
samples at 50 % overlap (Hanning window) yielding a frequency resolution of
$2^{14}$
samples at 50 % overlap (Hanning window) yielding a frequency resolution of
![]() $\unicode[STIX]{x0394}f=12.2$
Hz. Total measurement error accounting for sensor calibration, system error and test conditions is
$\unicode[STIX]{x0394}f=12.2$
Hz. Total measurement error accounting for sensor calibration, system error and test conditions is
![]() $\pm 2\,\%$
(
$\pm 2\,\%$
(
![]() $\pm 2.5\,\%$
at Mach 2). A more extensive account of the experimental procedures and early test rig development can be found in Chandola, Xin & Estruch-Samper (Reference Chandola, Huang and Estruch-Samper2017).
$\pm 2.5\,\%$
at Mach 2). A more extensive account of the experimental procedures and early test rig development can be found in Chandola, Xin & Estruch-Samper (Reference Chandola, Huang and Estruch-Samper2017).
3 Multi-scale interaction at Mach 3.9
3.1 Separation scaling approach
We start with the shortest step of
![]() $h=1.5~\text{mm}$
(
$h=1.5~\text{mm}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=0.3$
) and go on to progressively alter the scale of separation through
$h/\unicode[STIX]{x1D6FF}_{o}=0.3$
) and go on to progressively alter the scale of separation through
![]() $\unicode[STIX]{x0394}h=1.5~\text{mm}$
increments in step height and up to
$\unicode[STIX]{x0394}h=1.5~\text{mm}$
increments in step height and up to
![]() $h=22.5~\text{mm}$
for the reference highly separated case (
$h=22.5~\text{mm}$
for the reference highly separated case (
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
). The incoming flow conditions are hereby kept at
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
). The incoming flow conditions are hereby kept at
![]() $M_{e}=3.9$
, with undisturbed boundary-layer thickness growing from
$M_{e}=3.9$
, with undisturbed boundary-layer thickness growing from
![]() $\unicode[STIX]{x1D6FF}_{o}=3.8~\text{mm}$
to 4.5 mm within the range of reference separation locations – taken at the respective
$\unicode[STIX]{x1D6FF}_{o}=3.8~\text{mm}$
to 4.5 mm within the range of reference separation locations – taken at the respective
![]() $X_{U}^{\ast }=0$
for each case (see table 2). For presentation purposes, the following discussion centres around a selection of step heights, showing alternate cases in § 3; results for the complete range are then subsequently examined in the low-frequency analysis in § 5.
$X_{U}^{\ast }=0$
for each case (see table 2). For presentation purposes, the following discussion centres around a selection of step heights, showing alternate cases in § 3; results for the complete range are then subsequently examined in the low-frequency analysis in § 5.

Figure 6. Wall-pressure measurements: (a) mean axial pressure for alternate step heights in the range
![]() $0.3\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
and with edge Mach number
$0.3\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
and with edge Mach number
![]() $M_{e}=3.9$
(pressure at
$M_{e}=3.9$
(pressure at
![]() $\unicode[STIX]{x1D711}=180^{\circ }$
for
$\unicode[STIX]{x1D711}=180^{\circ }$
for
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
case shown with empty diamond symbols for reference), and (b) time-dependent pressure near separation
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
case shown with empty diamond symbols for reference), and (b) time-dependent pressure near separation
![]() $S_{1}$
for the reference case
$S_{1}$
for the reference case
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
(
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
(
![]() $\unicode[STIX]{x1D6FF}_{o,ref}=3.8~\text{mm}$
) and similar samples for (c) shortest step case with well-developed separation
$\unicode[STIX]{x1D6FF}_{o,ref}=3.8~\text{mm}$
) and similar samples for (c) shortest step case with well-developed separation
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
. Panel (a) shows alternate cases only; results on the total of 15 step heights (
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
. Panel (a) shows alternate cases only; results on the total of 15 step heights (
![]() $\unicode[STIX]{x0394}h/\unicode[STIX]{x1D6FF}_{o}\approx 0.4$
) at this Mach number are presented later in § 5.
$\unicode[STIX]{x0394}h/\unicode[STIX]{x1D6FF}_{o}\approx 0.4$
) at this Mach number are presented later in § 5.

Figure 7. Schlieren images of
![]() $M_{e}=3.9$
interactions with step height: (a)
$M_{e}=3.9$
interactions with step height: (a)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
, (b)
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
, (b)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.8$
, (c)
$h/\unicode[STIX]{x1D6FF}_{o}=1.8$
, (c)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=2.5$
, (d)
$h/\unicode[STIX]{x1D6FF}_{o}=2.5$
, (d)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=3.3$
, (e)
$h/\unicode[STIX]{x1D6FF}_{o}=3.3$
, (e)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=4.1$
and (f)
$h/\unicode[STIX]{x1D6FF}_{o}=4.1$
and (f)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.0$
; see figure 1 for
$h/\unicode[STIX]{x1D6FF}_{o}=5.0$
; see figure 1 for
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
case. Obtained using fine-resolution multiband horizontal filter and converted to grey scale; negative wall-normal density gradients
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
case. Obtained using fine-resolution multiband horizontal filter and converted to grey scale; negative wall-normal density gradients
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}y<0$
across separation shock and positive across shear layer
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}y<0$
across separation shock and positive across shear layer
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}y>0$
.
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}y>0$
.
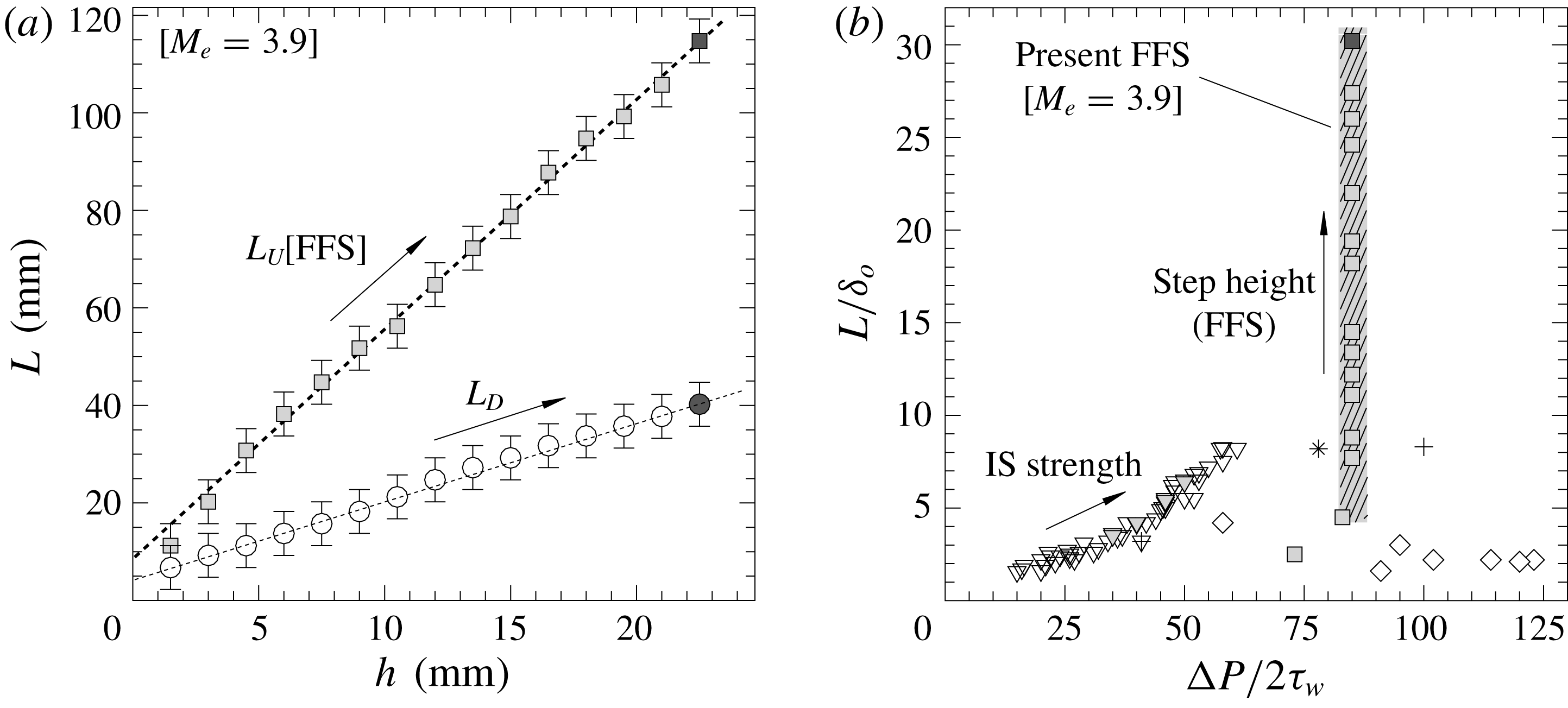
Figure 8. Variation in separation scale for complete range of
![]() $M_{e}=3.9$
interactions: (a) mean upstream and downstream separation lengths
$M_{e}=3.9$
interactions: (a) mean upstream and downstream separation lengths
![]() $L_{U}$
(squares) and
$L_{U}$
(squares) and
![]() $L_{D}$
(circles), with best linear fits indicated with dashed lines; (b) upstream separation length normalised by local boundary-layer thickness
$L_{D}$
(circles), with best linear fits indicated with dashed lines; (b) upstream separation length normalised by local boundary-layer thickness
![]() $L/\unicode[STIX]{x1D6FF}_{o}$
and plotted with respect to normalised shock intensity as
$L/\unicode[STIX]{x1D6FF}_{o}$
and plotted with respect to normalised shock intensity as
![]() $\unicode[STIX]{x0394}P/2\unicode[STIX]{x1D70F}_{w}$
together with incident shock cases (IS, gradient symbols) for different interaction strengths and further reference cases with symbols as listed in table 2. Arrows indicate tendency with increasing separation scale (see table 1). Reference highly separated case indicated with dark symbols.
$\unicode[STIX]{x0394}P/2\unicode[STIX]{x1D70F}_{w}$
together with incident shock cases (IS, gradient symbols) for different interaction strengths and further reference cases with symbols as listed in table 2. Arrows indicate tendency with increasing separation scale (see table 1). Reference highly separated case indicated with dark symbols.
The mean pressure levels along the interaction are presented in figure 6(a), with distance from step as
![]() $X_{S}=x$
–
$X_{S}=x$
–
![]() $x_{S}$
. The pressure rise upon separation remains similar for steps taller than the boundary-layer thickness, in all cases leading to a ratio
$x_{S}$
. The pressure rise upon separation remains similar for steps taller than the boundary-layer thickness, in all cases leading to a ratio
![]() $p_{p}/p_{u}=2.85$
between the undisturbed level of
$p_{p}/p_{u}=2.85$
between the undisturbed level of
![]() $p_{u}=9.84$
kPa and up to a common plateau
$p_{u}=9.84$
kPa and up to a common plateau
![]() $p_{p}$
. In accordance with free-interaction theory, the separating flow thus proves to be effectively independent of the source of separation – generally either due to an incident shock or surface geometry as in the present tests (e.g. see Delery & Marvin (Reference Delery and Marvin1986) for further insights on the free-interaction concept). The length of the isobaric (plateau) region is thus accordingly reduced for shorter steps and extends down to a location close near the corner, where a smaller – presumably counter-rotating – recirculation is formed (measurements over the step surface may be found in our earlier studies on the reference case
$p_{p}$
. In accordance with free-interaction theory, the separating flow thus proves to be effectively independent of the source of separation – generally either due to an incident shock or surface geometry as in the present tests (e.g. see Delery & Marvin (Reference Delery and Marvin1986) for further insights on the free-interaction concept). The length of the isobaric (plateau) region is thus accordingly reduced for shorter steps and extends down to a location close near the corner, where a smaller – presumably counter-rotating – recirculation is formed (measurements over the step surface may be found in our earlier studies on the reference case
![]() $h=22.5~\text{mm}$
,
$h=22.5~\text{mm}$
,
![]() $L/\unicode[STIX]{x1D6FF}_{o}=30.2$
). Following the compression across reattachment
$L/\unicode[STIX]{x1D6FF}_{o}=30.2$
). Following the compression across reattachment
![]() $R_{1}$
and the subsequent expansion over the step, another plateau is again found within the separation region behind, at
$R_{1}$
and the subsequent expansion over the step, another plateau is again found within the separation region behind, at
![]() ${\sim}0.2p_{u}$
; a last recompression then takes place upon downstream reattachment
${\sim}0.2p_{u}$
; a last recompression then takes place upon downstream reattachment
![]() $R_{2}$
as the flow recovers towards the undisturbed level.
$R_{2}$
as the flow recovers towards the undisturbed level.
As evidenced in the time-dependent pressure traces for the reference highly separated case in figure 6(b) (
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
), low-frequency fluctuations near the upstream separation location exhibit large-scale excursions between
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
), low-frequency fluctuations near the upstream separation location exhibit large-scale excursions between
![]() $p_{u}$
and higher levels approaching the plateau across
$p_{u}$
and higher levels approaching the plateau across
![]() $-0.04\leqslant X_{U}^{\ast }\leqslant 0.12$
– at a characteristic time scale of bubble pulsations
$-0.04\leqslant X_{U}^{\ast }\leqslant 0.12$
– at a characteristic time scale of bubble pulsations
![]() $T_{o}=1/f_{o}$
. For this case, the dominant low-frequency unsteadiness was found to be
$T_{o}=1/f_{o}$
. For this case, the dominant low-frequency unsteadiness was found to be
![]() $f_{o}=391$
Hz (
$f_{o}=391$
Hz (
![]() $St_{o,L}=0.070$
, with reference to velocity behind the shock, i.e. at outer shear layer edge
$St_{o,L}=0.070$
, with reference to velocity behind the shock, i.e. at outer shear layer edge
![]() $St_{o,L}=f_{o}L/U_{b}$
) and extending over several sensors along the upstream intermittency length
$St_{o,L}=f_{o}L/U_{b}$
) and extending over several sensors along the upstream intermittency length
![]() $L_{i}$
– defined as the length over which the separation-shock foot oscillates. Figure 6(c) further presents the respective signals for the
$L_{i}$
– defined as the length over which the separation-shock foot oscillates. Figure 6(c) further presents the respective signals for the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
interaction, i.e. the shortest step to exhibit a full rise to plateau. The plot here covers a period several times shorter than that above, both capturing an estimated 80 cycles each (
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
interaction, i.e. the shortest step to exhibit a full rise to plateau. The plot here covers a period several times shorter than that above, both capturing an estimated 80 cycles each (
![]() $t/T_{o}=80$
). While this offers some first evidence of the relatively higher pulsation frequencies
$t/T_{o}=80$
). While this offers some first evidence of the relatively higher pulsation frequencies
![]() $f_{o}$
for the shorter case, further insights are next to be drawn through spectral analysis.
$f_{o}$
for the shorter case, further insights are next to be drawn through spectral analysis.
Table 2. Reference STBLIs from past studies together with selection of present results. Configurations include: compression corner (CC), incident shock (IS), overexpanded nozzle (ON), blunt fin (BF) and forward-facing step (FFS).
![]() $Re_{h}$
,
$Re_{h}$
,
![]() $Re_{\unicode[STIX]{x1D6FF}}$
and
$Re_{\unicode[STIX]{x1D6FF}}$
and
![]() $Re_{\unicode[STIX]{x1D703}}$
are respectively with reference to step height
$Re_{\unicode[STIX]{x1D703}}$
are respectively with reference to step height
![]() $h$
, boundary-layer thickness
$h$
, boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}_{o}$
and momentum thickness
$\unicode[STIX]{x1D6FF}_{o}$
and momentum thickness
![]() $\unicode[STIX]{x1D703}_{o}$
, with conditions taken at the boundary-layer edge.
$\unicode[STIX]{x1D703}_{o}$
, with conditions taken at the boundary-layer edge.

a Indicates reports cited in the paper.
b Indicates cases to have documented an analogue shift from high to mid-frequencies over the separation and more closely evaluated in § 5.
In the schlieren images in figure 7, the separation shock is seen to maintain effectively the same angle of
![]() ${\sim}21^{\circ }$
for the different steps; a shear layer similar to that found in figure 1 develops upon separation and extends just over the upper edge of the step across all cases here as well. Increases in step height are seen to lead to an upstream shift of the separation location, with practically constant separation-shock strength – consistently with the associated pressure rise in figure 6(a) – thus producing an interaction of similar characteristics across multiple spatial scales. The variation in interaction scale attained over the complete range of configurations is summarised in figure 8(a) in terms of both the upstream FFS and downstream BFS separation lengths,
${\sim}21^{\circ }$
for the different steps; a shear layer similar to that found in figure 1 develops upon separation and extends just over the upper edge of the step across all cases here as well. Increases in step height are seen to lead to an upstream shift of the separation location, with practically constant separation-shock strength – consistently with the associated pressure rise in figure 6(a) – thus producing an interaction of similar characteristics across multiple spatial scales. The variation in interaction scale attained over the complete range of configurations is summarised in figure 8(a) in terms of both the upstream FFS and downstream BFS separation lengths,
![]() $L_{U}$
and
$L_{U}$
and
![]() $L_{D}$
, and where the respective mean locations (
$L_{D}$
, and where the respective mean locations (
![]() $X_{U}^{\ast }=0$
and
$X_{U}^{\ast }=0$
and
![]() $X_{D}^{\ast }=1$
) are selected based on the relative standard deviation maxima
$X_{D}^{\ast }=1$
) are selected based on the relative standard deviation maxima
![]() $(\unicode[STIX]{x1D70E}_{p}/p)_{max}$
within the intermittency range. Both are found to increase proportionally with step height across the complete range, starting with
$(\unicode[STIX]{x1D70E}_{p}/p)_{max}$
within the intermittency range. Both are found to increase proportionally with step height across the complete range, starting with
![]() $L_{U}/\unicode[STIX]{x1D6FF}_{o}=3.0$
for the shortest step (
$L_{U}/\unicode[STIX]{x1D6FF}_{o}=3.0$
for the shortest step (
![]() $h=1.5~\text{mm}$
,
$h=1.5~\text{mm}$
,
![]() $h/\unicode[STIX]{x1D6FF}_{o}=0.3$
), and up to an order of magnitude greater for the reference case
$h/\unicode[STIX]{x1D6FF}_{o}=0.3$
), and up to an order of magnitude greater for the reference case
![]() $L_{U}/\unicode[STIX]{x1D6FF}_{o}=30.2$
(
$L_{U}/\unicode[STIX]{x1D6FF}_{o}=30.2$
(
![]() $h=22.5~\text{mm}$
,
$h=22.5~\text{mm}$
,
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
). The downstream separation length scales approximately as
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
). The downstream separation length scales approximately as
![]() $L_{D}\approx 1/3L_{U}$
.
$L_{D}\approx 1/3L_{U}$
.
A number of reference studies to have documented STBLI unsteadiness through different approaches/configurations are listed in table 2. Figure 8(b) plots the
![]() $L/\unicode[STIX]{x1D6FF}_{o}$
ratio across these studies as a function of
$L/\unicode[STIX]{x1D6FF}_{o}$
ratio across these studies as a function of
![]() $\unicode[STIX]{x0394}P/2\unicode[STIX]{x1D70F}_{w}$
– taken as a measure of separation-shock intensity, where
$\unicode[STIX]{x0394}P/2\unicode[STIX]{x1D70F}_{w}$
– taken as a measure of separation-shock intensity, where
![]() $\unicode[STIX]{x1D70F}_{w}$
is wall shear stress (a practical parameter consistent with free-interaction considerations, though simplistic in the scaling of separation). The plot incorporates a particularly large compilation of incident shock interactions considered in the scaling analysis of Souverein et al. (Reference Souverein, Bakker and Dupont2013), at Mach 2.3 and
$\unicode[STIX]{x1D70F}_{w}$
is wall shear stress (a practical parameter consistent with free-interaction considerations, though simplistic in the scaling of separation). The plot incorporates a particularly large compilation of incident shock interactions considered in the scaling analysis of Souverein et al. (Reference Souverein, Bakker and Dupont2013), at Mach 2.3 and
![]() $Re_{e}/m=5.3\times 10^{6}$
(
$Re_{e}/m=5.3\times 10^{6}$
(
![]() $Re_{\unicode[STIX]{x1D6FF}}=5.8\times 10^{4}$
) and with different incident shock strengths. Further comparison with other configurations and at a wider range of flow conditions (see table 2) finds separation lengths also within
$Re_{\unicode[STIX]{x1D6FF}}=5.8\times 10^{4}$
) and with different incident shock strengths. Further comparison with other configurations and at a wider range of flow conditions (see table 2) finds separation lengths also within
![]() $L/\unicode[STIX]{x1D6FF}_{o}\approx 1$
–8 and with varying shock intensities. Here, the flow upon separation (across
$L/\unicode[STIX]{x1D6FF}_{o}\approx 1$
–8 and with varying shock intensities. Here, the flow upon separation (across
![]() $S_{1}$
) is subjected to a common
$S_{1}$
) is subjected to a common
![]() $\unicode[STIX]{x0394}P/2\unicode[STIX]{x1D70F}_{w}$
for cases
$\unicode[STIX]{x0394}P/2\unicode[STIX]{x1D70F}_{w}$
for cases
![]() $h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
, thus decoupling the change in interaction scale from the upstream separation-shock intensity and other related variables of importance e.g. velocity behind the shock
$h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
, thus decoupling the change in interaction scale from the upstream separation-shock intensity and other related variables of importance e.g. velocity behind the shock
![]() $U_{b}$
, associated pressure rise
$U_{b}$
, associated pressure rise
![]() $p_{p}/p_{u}$
, density rise across the shock
$p_{p}/p_{u}$
, density rise across the shock
![]() $\unicode[STIX]{x1D70C}_{b}/\unicode[STIX]{x1D70C}_{e}$
, etc. This is in part achieved given the high deflection angle of
$\unicode[STIX]{x1D70C}_{b}/\unicode[STIX]{x1D70C}_{e}$
, etc. This is in part achieved given the high deflection angle of
![]() $\unicode[STIX]{x1D6FC}=90^{\circ }$
(FFS), where
$\unicode[STIX]{x1D6FC}=90^{\circ }$
(FFS), where
![]() $\unicode[STIX]{x1D6FC}$
is well above the inviscid detached shock condition and renders obstacle height
$\unicode[STIX]{x1D6FC}$
is well above the inviscid detached shock condition and renders obstacle height
![]() $h$
as the primary variable dictating interaction scale, and hence separated mass (§ 5.1). The present cases are also characterised for the high Reynolds number of
$h$
as the primary variable dictating interaction scale, and hence separated mass (§ 5.1). The present cases are also characterised for the high Reynolds number of
![]() $Re_{e}/m=6.1\times 10^{7}$
(
$Re_{e}/m=6.1\times 10^{7}$
(
![]() $Re_{\unicode[STIX]{x1D6FF}}=2.3\times 10^{5}$
).
$Re_{\unicode[STIX]{x1D6FF}}=2.3\times 10^{5}$
).
3.2 Unsteadiness of step-induced separation

Figure 9. Pressure power spectral density (PSD) within upstream separation region for
![]() $M_{e}=3.9$
cases with step height: (a)
$M_{e}=3.9$
cases with step height: (a)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
, (b)
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
, (b)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.8$
, (c)
$h/\unicode[STIX]{x1D6FF}_{o}=1.8$
, (c)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=2.5$
, (d)
$h/\unicode[STIX]{x1D6FF}_{o}=2.5$
, (d)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=3.3$
, (e)
$h/\unicode[STIX]{x1D6FF}_{o}=3.3$
, (e)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=4.1$
and (f)
$h/\unicode[STIX]{x1D6FF}_{o}=4.1$
and (f)
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.0$
.
$h/\unicode[STIX]{x1D6FF}_{o}=5.0$
.
![]() $X_{U}^{\ast }$
locations are normalised with the respective
$X_{U}^{\ast }$
locations are normalised with the respective
![]() $L_{U}$
(within
$L_{U}$
(within
![]() $\pm 0.05$
accuracy). Arrows follow shear layer evolution and grey line indicates PSD levels immediately preceding the shear layer’s inception.
$\pm 0.05$
accuracy). Arrows follow shear layer evolution and grey line indicates PSD levels immediately preceding the shear layer’s inception.
Figure 9 presents the pressure power spectral density (PSD) in premultiplied form
![]() $fG_{xx}$
for alternate cases within the range of scales involving well-developed separation,
$fG_{xx}$
for alternate cases within the range of scales involving well-developed separation,
![]() $h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
. For direct comparison with the reference highly separated interaction, the spectra are scaled with respect to the maximum PSD levels just ahead of the step for this case,
$h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
. For direct comparison with the reference highly separated interaction, the spectra are scaled with respect to the maximum PSD levels just ahead of the step for this case,
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
(at
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
(at
![]() $X_{U}^{\ast }\approx 0.98$
). Each of the panels in the figure corresponds to a different step height and presents the spectra in
$X_{U}^{\ast }\approx 0.98$
). Each of the panels in the figure corresponds to a different step height and presents the spectra in
![]() $\unicode[STIX]{x0394}X_{U}^{\ast }\approx 0.2$
steps between separation (
$\unicode[STIX]{x0394}X_{U}^{\ast }\approx 0.2$
steps between separation (
![]() $X_{U}^{\ast }=0$
) and just ahead of the step (
$X_{U}^{\ast }=0$
) and just ahead of the step (
![]() $X_{U}^{\ast }\approx 0.98$
) – with locations selected within
$X_{U}^{\ast }\approx 0.98$
) – with locations selected within
![]() $\pm 0.05$
accuracy. For the
$\pm 0.05$
accuracy. For the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
case (figure 9
a), the high frequencies associated with the shear layer appear relatively weak as it starts to be incipiently formed; the narrowband shear layer levels are then enhanced for taller steps (figure 9(b, c) as the shift to lower frequencies becomes more clearly defined. This tendency is maintained with subsequent increases in step height,
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
case (figure 9
a), the high frequencies associated with the shear layer appear relatively weak as it starts to be incipiently formed; the narrowband shear layer levels are then enhanced for taller steps (figure 9(b, c) as the shift to lower frequencies becomes more clearly defined. This tendency is maintained with subsequent increases in step height,
![]() $h/\unicode[STIX]{x1D6FF}_{o}=4.1$
to 5.0 (figure 9
d–f), with different sensors capturing analogue stages of its growth across tests. For all the cases, the spectra at separation
$h/\unicode[STIX]{x1D6FF}_{o}=4.1$
to 5.0 (figure 9
d–f), with different sensors capturing analogue stages of its growth across tests. For all the cases, the spectra at separation
![]() $X_{U}^{\ast }=0$
is primarily concentrated at low frequencies (
$X_{U}^{\ast }=0$
is primarily concentrated at low frequencies (
![]() $10^{2}$
–
$10^{2}$
–
![]() $10^{3}$
Hz), with similar low-frequency levels obtained (integrated up to
$10^{3}$
Hz), with similar low-frequency levels obtained (integrated up to
![]() $10^{3}$
Hz) just upstream of the step, yet following a more broadband distribution and superimposed on the shear layer spectra. The bulk of the energy is thus primarily associated with shear layer disturbance levels at the mid/high range of the spectrum (
$10^{3}$
Hz) just upstream of the step, yet following a more broadband distribution and superimposed on the shear layer spectra. The bulk of the energy is thus primarily associated with shear layer disturbance levels at the mid/high range of the spectrum (
![]() $10^{4}$
–
$10^{4}$
–
![]() $10^{5}$
Hz) and with negligible low-frequency component. As seen in the schlieren, shocklets effectively emanate from shear layer eddies due to their supersonic convection velocity, i.e. relative to the inner (reverse) and outer flow. The shear layer overall remains well defined, with the trends evidencing the influence of local perturbations radiated by large-scale eddy structures as they evolve along the bubble, expectedly with streamwise directivity – hence the cumulative enhancement in spectral levels – and with point-to-point coherence remaining at
$10^{5}$
Hz) and with negligible low-frequency component. As seen in the schlieren, shocklets effectively emanate from shear layer eddies due to their supersonic convection velocity, i.e. relative to the inner (reverse) and outer flow. The shear layer overall remains well defined, with the trends evidencing the influence of local perturbations radiated by large-scale eddy structures as they evolve along the bubble, expectedly with streamwise directivity – hence the cumulative enhancement in spectral levels – and with point-to-point coherence remaining at
![]() $C_{x,1-x}\approx 0.65$
.
$C_{x,1-x}\approx 0.65$
.

Figure 10. Contours of pressure PSD in the (f,x)-plane over axisymmetric step at Mach 3.9 (FFS as per figure 9), together with cross-correlation at selected locations and with respect to separation
![]() $\unicode[STIX]{x1D70C}_{ox}$
(near plateau start
$\unicode[STIX]{x1D70C}_{ox}$
(near plateau start
![]() $X_{U}^{\ast }=0.2$
, just ahead of step
$X_{U}^{\ast }=0.2$
, just ahead of step
![]() $X_{U}^{\ast }\approx 0.98$
and at downstream reattachment
$X_{U}^{\ast }\approx 0.98$
and at downstream reattachment
![]() $X_{D}^{\ast }=1$
). Detailed cross-correlations may be found in Chandola et al. (Reference Chandola, Huang and Estruch-Samper2017) for the reference large-scale interaction,
$X_{D}^{\ast }=1$
). Detailed cross-correlations may be found in Chandola et al. (Reference Chandola, Huang and Estruch-Samper2017) for the reference large-scale interaction,
![]() $L/\unicode[STIX]{x1D6FF}_{o}=30.2$
.
$L/\unicode[STIX]{x1D6FF}_{o}=30.2$
.
The contour maps in figure 10 comprise the PSD of the signals over the complete measurement range and capture in detail the separated shear layer’s influence, seen to emerge at locations close downstream of separation and then extending along the recirculation length. In the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
case (
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
case (
![]() $L_{U}=8\unicode[STIX]{x1D6FF}_{o}$
), the shear layer is relatively short but its effect becomes more clearly defined as the scale of separation increases with taller steps. The low-frequency pulsations near separation
$L_{U}=8\unicode[STIX]{x1D6FF}_{o}$
), the shear layer is relatively short but its effect becomes more clearly defined as the scale of separation increases with taller steps. The low-frequency pulsations near separation
![]() $X_{U}^{\ast }=0$
, of order
$X_{U}^{\ast }=0$
, of order
![]() $10^{2}$
–
$10^{2}$
–
![]() $10^{3}$
Hz, remain narrowband and shift to lower frequencies for larger scales (see figure 9). The dominant distribution at low frequencies, due to the large-scale bubble pulsations, is consistently documented over several sensors along the upstream intermittency length – increasing from
$10^{3}$
Hz, remain narrowband and shift to lower frequencies for larger scales (see figure 9). The dominant distribution at low frequencies, due to the large-scale bubble pulsations, is consistently documented over several sensors along the upstream intermittency length – increasing from
![]() $L_{i}=10~\text{mm}$
to
$L_{i}=10~\text{mm}$
to
![]() $17~\text{mm}$
between
$17~\text{mm}$
between
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
and 5.9 – based on a combined wall-pressure and schlieren-based analysis (Estruch-Samper et al.
Reference Estruch-Samper, Lawson, Macmanus, Garry and Stollery2008). To be specific, it is worth noting that the wall spectra not only reflect a low-frequency dominance over the (shock foot’s) intermittency length but also slightly downstream of it, where large fluctuations above the reference level (
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
and 5.9 – based on a combined wall-pressure and schlieren-based analysis (Estruch-Samper et al.
Reference Estruch-Samper, Lawson, Macmanus, Garry and Stollery2008). To be specific, it is worth noting that the wall spectra not only reflect a low-frequency dominance over the (shock foot’s) intermittency length but also slightly downstream of it, where large fluctuations above the reference level (
![]() ${>}p_{u}$
) are induced. The low-frequency unsteadiness associated with separation bubble pulsations is as well evidenced close ahead of the step
${>}p_{u}$
) are induced. The low-frequency unsteadiness associated with separation bubble pulsations is as well evidenced close ahead of the step
![]() $X_{U}^{\ast }\approx 0.98$
, found relatively broadband below
$X_{U}^{\ast }\approx 0.98$
, found relatively broadband below
![]() ${\sim}10^{3}$
Hz and overlapped with the local shear layer instabilities. The flow in the relaxation region downstream of reattachment then progressively adopts a higher-frequency dominance as it returns to the base levels. The spectra near
${\sim}10^{3}$
Hz and overlapped with the local shear layer instabilities. The flow in the relaxation region downstream of reattachment then progressively adopts a higher-frequency dominance as it returns to the base levels. The spectra near
![]() $X_{D}^{\ast }=1$
also exhibit a tendency towards lower pulsation frequencies for larger BFS scales, yet at approximately an order of magnitude higher than in the upstream separation (FFS).
$X_{D}^{\ast }=1$
also exhibit a tendency towards lower pulsation frequencies for larger BFS scales, yet at approximately an order of magnitude higher than in the upstream separation (FFS).
Also shown beside the contours are the cross-correlations with respect to separation
![]() $\unicode[STIX]{x1D70C}_{ox}(\unicode[STIX]{x1D70F})$
, which rely on prior low-pass filtering of the signals at 1 kHz to assess the low-frequency dynamics along the interaction (figure 10). Both the pressure near shear layer inception and downstream reattachment,
$\unicode[STIX]{x1D70C}_{ox}(\unicode[STIX]{x1D70F})$
, which rely on prior low-pass filtering of the signals at 1 kHz to assess the low-frequency dynamics along the interaction (figure 10). Both the pressure near shear layer inception and downstream reattachment,
![]() $X_{U}^{\ast }=0.2$
and
$X_{U}^{\ast }=0.2$
and
![]() $X_{D}^{\ast }=1$
, are in positive correlation with separation
$X_{D}^{\ast }=1$
, are in positive correlation with separation
![]() $\unicode[STIX]{x1D70C}_{ox}>0$
, with upstream shifts of the separation shock (hence pressure increases at
$\unicode[STIX]{x1D70C}_{ox}>0$
, with upstream shifts of the separation shock (hence pressure increases at
![]() $X_{U}^{\ast }=0$
) briefly preceded by upstream travelling perturbations, felt near shear layer inception, and subsequently leading to a shrinking of the downstream BFS (pressure at
$X_{U}^{\ast }=0$
) briefly preceded by upstream travelling perturbations, felt near shear layer inception, and subsequently leading to a shrinking of the downstream BFS (pressure at
![]() $X_{D}^{\ast }=1$
increases). Consistently across the range, the signal just ahead of the step
$X_{D}^{\ast }=1$
increases). Consistently across the range, the signal just ahead of the step
![]() $X_{U}^{\ast }\approx 0.98$
instead remains in negative correlation and time delay (
$X_{U}^{\ast }\approx 0.98$
instead remains in negative correlation and time delay (
![]() $\unicode[STIX]{x1D70C}_{ox}<0$
,
$\unicode[STIX]{x1D70C}_{ox}<0$
,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}<0$
) – i.e. with downstream separation-shock displacements being quickly followed with pressure increases near the step. For all cases, the separation/reattachment shock motions upstream of the step (
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}<0$
) – i.e. with downstream separation-shock displacements being quickly followed with pressure increases near the step. For all cases, the separation/reattachment shock motions upstream of the step (
![]() $S_{1}$
,
$S_{1}$
,
![]() $R_{1}$
) are thus characterised for their out-of-phase dynamics throughout the separation’s decay–growth cycle, with upstream shock displacements in synchronisation with downstream motions of the reattachment shock and vice versa.
$R_{1}$
) are thus characterised for their out-of-phase dynamics throughout the separation’s decay–growth cycle, with upstream shock displacements in synchronisation with downstream motions of the reattachment shock and vice versa.
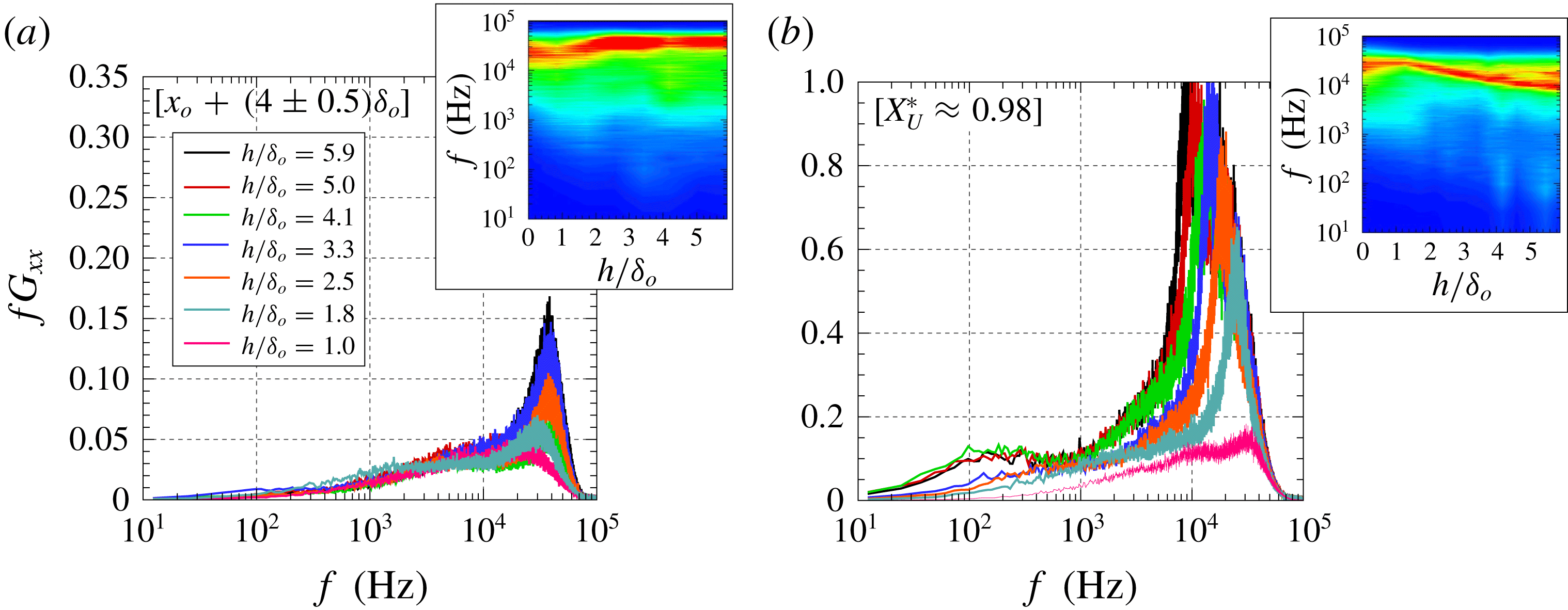
Figure 11. Pressure PSD for
![]() $M_{e}=3.9$
interaction cases in the range
$M_{e}=3.9$
interaction cases in the range
![]() $1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
: (a) at shear layer inception
$1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
: (a) at shear layer inception
![]() $x_{o}+(4\pm 0.5)\unicode[STIX]{x1D6FF}_{o}$
and (b) just ahead of the step
$x_{o}+(4\pm 0.5)\unicode[STIX]{x1D6FF}_{o}$
and (b) just ahead of the step
![]() $X_{U}^{\ast }\approx 0.98$
(at its departure from the bubble). Levels in pressure PSD contours match the respective
$X_{U}^{\ast }\approx 0.98$
(at its departure from the bubble). Levels in pressure PSD contours match the respective
![]() $\log (fG_{xx})$
range up to given maxima. Inception correspond to locations ranging from
$\log (fG_{xx})$
range up to given maxima. Inception correspond to locations ranging from
![]() $X_{U}^{\ast }=0.16$
to 0.53 (from
$X_{U}^{\ast }=0.16$
to 0.53 (from
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
to 1.0).
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
to 1.0).

Figure 12. Pressure PSD for
![]() $M_{e}=3.9$
interaction cases in the range
$M_{e}=3.9$
interaction cases in the range
![]() $1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
at: (a) upstream separation
$1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
at: (a) upstream separation
![]() $X_{U}^{\ast }=0$
and (b) downstream reattachment locations
$X_{U}^{\ast }=0$
and (b) downstream reattachment locations
![]() $X_{D}^{\ast }=1$
. Normalised with respect to local variance (
$X_{D}^{\ast }=1$
. Normalised with respect to local variance (
![]() $\unicode[STIX]{x1D70E}_{S}^{2}$
,
$\unicode[STIX]{x1D70E}_{S}^{2}$
,
![]() $\unicode[STIX]{x1D70E}_{R}^{2}$
), where subscripts
$\unicode[STIX]{x1D70E}_{R}^{2}$
), where subscripts
![]() $_{S}$
and
$_{S}$
and
![]() $_{R}$
refer accordingly to upstream separation (
$_{R}$
refer accordingly to upstream separation (
![]() $S_{1}$
) and downstream reattachment (
$S_{1}$
) and downstream reattachment (
![]() $R_{2}$
). Line legends as per figure 11; arrows indicate shift to lower frequencies with increasing step height and grey region delimits dominant frequencies between the
$R_{2}$
). Line legends as per figure 11; arrows indicate shift to lower frequencies with increasing step height and grey region delimits dominant frequencies between the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
and
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
and
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
cases (from higher to lower characteristic frequencies).
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
cases (from higher to lower characteristic frequencies).
Figure 11(a) presents an overlap of the spectra at the inception location, where the onset of high-frequency instabilities is first documented, at approximately
![]() ${\sim}0.5L_{i}+2\unicode[STIX]{x1D6FF}_{o}$
downstream of
${\sim}0.5L_{i}+2\unicode[STIX]{x1D6FF}_{o}$
downstream of
![]() $X_{U}^{\ast }=0$
(where
$X_{U}^{\ast }=0$
(where
![]() $L_{i}/\unicode[STIX]{x1D6FF}_{o}=2.4$
to 4.5, accordingly from
$L_{i}/\unicode[STIX]{x1D6FF}_{o}=2.4$
to 4.5, accordingly from
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
to 5.9 as per the schlieren-based analysis), close downstream of the shock’s oscillation range. The distribution remains highly similar for the range of cases here
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
to 5.9 as per the schlieren-based analysis), close downstream of the shock’s oscillation range. The distribution remains highly similar for the range of cases here
![]() $h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
, with an overlap of the inception levels at
$h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
, with an overlap of the inception levels at
![]() $f_{i}=37.5\pm 2~\text{kHz}$
,
$f_{i}=37.5\pm 2~\text{kHz}$
,
![]() $St_{i,\unicode[STIX]{x1D6FF}}=0.21\pm 5\,\%$
(where
$St_{i,\unicode[STIX]{x1D6FF}}=0.21\pm 5\,\%$
(where
![]() $St_{i,\unicode[STIX]{x1D6FF}}=f_{i}\unicode[STIX]{x1D6FF}_{o}/U_{e}$
). Essentially, the incipient development of the shear layer appears to be largely independent of both downstream geometry and the scale of separation, this being also consistent with the negligible variations in separation-shock strength and associated pressure rise (figures 6 and 7) – again in coherence with free-interaction arguments, yet with
$St_{i,\unicode[STIX]{x1D6FF}}=f_{i}\unicode[STIX]{x1D6FF}_{o}/U_{e}$
). Essentially, the incipient development of the shear layer appears to be largely independent of both downstream geometry and the scale of separation, this being also consistent with the negligible variations in separation-shock strength and associated pressure rise (figures 6 and 7) – again in coherence with free-interaction arguments, yet with
![]() $\unicode[STIX]{x1D6FF}_{o}$
being the most immediate reference scale (as later observed, § 5). As shown for the same cases in figure 11(b), a much different tendency is evidenced just ahead of the step
$\unicode[STIX]{x1D6FF}_{o}$
being the most immediate reference scale (as later observed, § 5). As shown for the same cases in figure 11(b), a much different tendency is evidenced just ahead of the step
![]() $X_{U}^{\ast }\approx 0.98$
, where gradually lower shedding frequencies are found for larger interactions, with accordingly enhanced disturbance levels.
$X_{U}^{\ast }\approx 0.98$
, where gradually lower shedding frequencies are found for larger interactions, with accordingly enhanced disturbance levels.
The variation in low-frequency unsteadiness
![]() $f_{o}$
is further evaluated in figure 12, in this instance with premultiplied spectra normalised by local variance
$f_{o}$
is further evaluated in figure 12, in this instance with premultiplied spectra normalised by local variance
![]() $\unicode[STIX]{x1D70E}_{x}^{2}$
to account for relative differences in intermittency with sensor location; the values of
$\unicode[STIX]{x1D70E}_{x}^{2}$
to account for relative differences in intermittency with sensor location; the values of
![]() $f_{o}$
extracted next are within
$f_{o}$
extracted next are within
![]() $\pm 2\,\%$
to
$\pm 2\,\%$
to
![]() $\pm 9\,\%$
uncertainty for the FFS at
$\pm 9\,\%$
uncertainty for the FFS at
![]() $X_{U}^{\ast }=0$
(from shorter to taller steps), and approximately
$X_{U}^{\ast }=0$
(from shorter to taller steps), and approximately
![]() $\pm 10\,\%$
for the BFS at
$\pm 10\,\%$
for the BFS at
![]() $X_{D}^{\ast }=1$
. With increasing interaction scale, upstream bubble pulsations are found to shift rapidly from 1872 Hz to 1250 Hz between
$X_{D}^{\ast }=1$
. With increasing interaction scale, upstream bubble pulsations are found to shift rapidly from 1872 Hz to 1250 Hz between
![]() $h/\unicode[STIX]{x1D6FF}_{o}=0.3$
and
$h/\unicode[STIX]{x1D6FF}_{o}=0.3$
and
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
(
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
(
![]() $St_{o,L}=0.033$
to 0.066). The tendency is then slightly moderated for taller steps as separation length
$St_{o,L}=0.033$
to 0.066). The tendency is then slightly moderated for taller steps as separation length
![]() $L_{U}$
increases by over a factor
$L_{U}$
increases by over a factor
![]() $\times 3$
between the
$\times 3$
between the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
and
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
and
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
cases, with
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
cases, with
![]() $f_{o}$
reduced from 1250 Hz to 391 Hz (
$f_{o}$
reduced from 1250 Hz to 391 Hz (
![]() $St_{o,L}=0.066$
to 0.070). A similar effect is found at
$St_{o,L}=0.066$
to 0.070). A similar effect is found at
![]() $X_{D}^{\ast }=1$
, where the dominant frequency of
$X_{D}^{\ast }=1$
, where the dominant frequency of
![]() $9.27~\text{kHz}$
for the
$9.27~\text{kHz}$
for the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
step drops to 3.55 kHz by
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
step drops to 3.55 kHz by
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
, a high
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
, a high
![]() $St_{o,L}=0.010$
–0.21 taking reference velocity
$St_{o,L}=0.010$
–0.21 taking reference velocity
![]() ${\sim}U_{b}$
(yet noting this is here overestimated given the local expansion upon
${\sim}U_{b}$
(yet noting this is here overestimated given the local expansion upon
![]() $S_{2}$
). Overall, except for the two shorter steps
$S_{2}$
). Overall, except for the two shorter steps
![]() $h<\unicode[STIX]{x1D6FF}_{o}$
(§ 3.4), the Strouhal numbers are for instance much greater than the values of
$h<\unicode[STIX]{x1D6FF}_{o}$
(§ 3.4), the Strouhal numbers are for instance much greater than the values of
![]() $St_{o,L}\approx 0.032\pm 20\,\%$
reported for the incident shock interactions in table 2 – noting relatively enhanced mass depletion is expected here, in part given the later shear layer ejection location
$St_{o,L}\approx 0.032\pm 20\,\%$
reported for the incident shock interactions in table 2 – noting relatively enhanced mass depletion is expected here, in part given the later shear layer ejection location
![]() $X_{ej}^{\ast }=x_{ej}/L$
, as further elaborated in § 5. Estimates based on the upstream intermittency length (an
$X_{ej}^{\ast }=x_{ej}/L$
, as further elaborated in § 5. Estimates based on the upstream intermittency length (an
![]() $St_{o,Li}=f_{o}L_{i}/U_{e}$
of 0.018 for the
$St_{o,Li}=f_{o}L_{i}/U_{e}$
of 0.018 for the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
case and 0.010 for
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
case and 0.010 for
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
) are in closer agreement with the correlations of about
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
) are in closer agreement with the correlations of about
![]() $St_{o,Li}\approx 0.02\pm 0.01$
reported in Clemens & Narayanaswamy (Reference Clemens and Narayanaswamy2014) but increasingly differ for the larger-scale separations. Taking the upstream shock velocity as
$St_{o,Li}\approx 0.02\pm 0.01$
reported in Clemens & Narayanaswamy (Reference Clemens and Narayanaswamy2014) but increasingly differ for the larger-scale separations. Taking the upstream shock velocity as
![]() $v_{S}=2f_{o}L_{i}$
– assuming the shock velocity across
$v_{S}=2f_{o}L_{i}$
– assuming the shock velocity across
![]() $L_{i}$
to be constant during upstream/downstream sweeps – the respective estimates are
$L_{i}$
to be constant during upstream/downstream sweeps – the respective estimates are
![]() $25.4~\text{m}~\text{s}^{-1}$
(
$25.4~\text{m}~\text{s}^{-1}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
) and
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
) and
![]() $13.2~\text{m}~\text{s}^{-1}$
(
$13.2~\text{m}~\text{s}^{-1}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
), accordingly
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
), accordingly
![]() $3.7\,\%U_{e}$
and
$3.7\,\%U_{e}$
and
![]() $1.9\,\%U_{e}$
, with the shock thus oscillating on average at lower speed for larger interactions.
$1.9\,\%U_{e}$
, with the shock thus oscillating on average at lower speed for larger interactions.

Figure 13. Streamwise evolution of the separated shear layer for
![]() $M_{e}=3.9$
interactions: (a) schematic of highly separated interaction (scaled to fit reference highly separated case,
$M_{e}=3.9$
interactions: (a) schematic of highly separated interaction (scaled to fit reference highly separated case,
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
), (b) characteristic frequency
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
), (b) characteristic frequency
![]() $f_{ch}$
, peak from pressure PSD (c) phase velocity associated with dominant disturbance
$f_{ch}$
, peak from pressure PSD (c) phase velocity associated with dominant disturbance
![]() $v_{\unicode[STIX]{x1D719}}$
and (d) associated wavelength
$v_{\unicode[STIX]{x1D719}}$
and (d) associated wavelength
![]() $\unicode[STIX]{x1D706}_{w}$
. Schematic indicates upstream intermittency length
$\unicode[STIX]{x1D706}_{w}$
. Schematic indicates upstream intermittency length
![]() $L_{i,U}$
, downstream intermittency length
$L_{i,U}$
, downstream intermittency length
![]() $L_{i,D}$
and velocity behind separation shock
$L_{i,D}$
and velocity behind separation shock
![]() $U_{b}$
.
$U_{b}$
.
3.3 Shear layer evolution
The evolutions of characteristic shear layer disturbances
![]() $f_{ch}$
, corresponding to the maxima extracted from the premultiplied spectra
$f_{ch}$
, corresponding to the maxima extracted from the premultiplied spectra
![]() $fG_{xx}$
, are presented in figure 13. Upon separation,
$fG_{xx}$
, are presented in figure 13. Upon separation,
![]() $f_{ch}$
rises rapidly by two orders of magnitude between the low-frequency fluctuations associated with bubble pulsations and the shear layer inception frequencies. The latter effectively comprise the highest frequencies along the interaction and emerge close downstream of separation at a similar level (
$f_{ch}$
rises rapidly by two orders of magnitude between the low-frequency fluctuations associated with bubble pulsations and the shear layer inception frequencies. The latter effectively comprise the highest frequencies along the interaction and emerge close downstream of separation at a similar level (
![]() $St_{i,\unicode[STIX]{x1D6FF}}=0.21\pm 5\,\%$
) to then decrease monotonically towards the step. The gradually lower frequencies near reattachment
$St_{i,\unicode[STIX]{x1D6FF}}=0.21\pm 5\,\%$
) to then decrease monotonically towards the step. The gradually lower frequencies near reattachment
![]() $R_{1}$
(figure 11
b) are thus noted to result from the longer shear layer development path (up to its ejection) for larger interaction scales, effectively enabling its evolution to lower rates by the time it approaches this location. Together with the above observations on the shear layer inception frequencies (figure 11
a), this is a key outcome from the present results which later serves to elucidate important aspects of the mass entrainment dynamics (§ 5). A similar tendency is also noted close behind the step, where the frequencies of the downstream separated shear layer appear to decrease at a slower rate (discernible for larger interactions), followed by the lower-frequency unsteadiness associated with downstream bubble pulsations near reattachment
$R_{1}$
(figure 11
b) are thus noted to result from the longer shear layer development path (up to its ejection) for larger interaction scales, effectively enabling its evolution to lower rates by the time it approaches this location. Together with the above observations on the shear layer inception frequencies (figure 11
a), this is a key outcome from the present results which later serves to elucidate important aspects of the mass entrainment dynamics (§ 5). A similar tendency is also noted close behind the step, where the frequencies of the downstream separated shear layer appear to decrease at a slower rate (discernible for larger interactions), followed by the lower-frequency unsteadiness associated with downstream bubble pulsations near reattachment
![]() $R_{2}$
and the eventual return to higher frequencies within the relaxation region.
$R_{2}$
and the eventual return to higher frequencies within the relaxation region.
The phase velocities in figure 13(c) are also found to exhibit a similar trend across the range of interaction scales, with
![]() $v_{\unicode[STIX]{x1D719}}\approx (0.58\pm 0.02)U_{b}$
near the shear layer inception, where
$v_{\unicode[STIX]{x1D719}}\approx (0.58\pm 0.02)U_{b}$
near the shear layer inception, where
![]() $v_{\unicode[STIX]{x1D719}}=2\unicode[STIX]{x03C0}f\unicode[STIX]{x1D709}/\unicode[STIX]{x1D719}$
and
$v_{\unicode[STIX]{x1D719}}=2\unicode[STIX]{x03C0}f\unicode[STIX]{x1D709}/\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}$
is the phase deduced from the cross-spectra between adjacent sensor locations. The subsequent reduction in convection velocity down to
$\unicode[STIX]{x1D719}$
is the phase deduced from the cross-spectra between adjacent sensor locations. The subsequent reduction in convection velocity down to
![]() $(0.42\pm 0.02)U_{b}$
is associated with the dissymmetry of the shear layer, where
$(0.42\pm 0.02)U_{b}$
is associated with the dissymmetry of the shear layer, where
![]() $M_{c}=v_{\unicode[STIX]{x1D719}}/c_{b}$
is convection Mach number (
$M_{c}=v_{\unicode[STIX]{x1D719}}/c_{b}$
is convection Mach number (
![]() $c_{b}$
is speed of sound behind the shock). As such, the relative Mach number with respect to the outer edge
$c_{b}$
is speed of sound behind the shock). As such, the relative Mach number with respect to the outer edge
![]() $\unicode[STIX]{x0394}M_{\unicode[STIX]{x1D719},b}=(U_{b}-v_{\unicode[STIX]{x1D719}})/c_{b}$
in turn increases in the streamwise direction. The dissymmetry is similar in nature to that documented in a number of past mixing layer studies (e.g. Papamoschou & Roshko Reference Papamoschou and Roshko1988, Dimotakis Reference Dimotakis1991, Slessor, Zhuang & Dimotakis Reference Slessor, Zhuang and Dimotakis2000), with the shear layer being here effectively wall bounded below its lower edge and comprising the upper layers of the recirculation. Within the context of STBLIs, the present results find the tendency to attain the symmetry level by the middle of the interaction for all cases (assumed
$\unicode[STIX]{x0394}M_{\unicode[STIX]{x1D719},b}=(U_{b}-v_{\unicode[STIX]{x1D719}})/c_{b}$
in turn increases in the streamwise direction. The dissymmetry is similar in nature to that documented in a number of past mixing layer studies (e.g. Papamoschou & Roshko Reference Papamoschou and Roshko1988, Dimotakis Reference Dimotakis1991, Slessor, Zhuang & Dimotakis Reference Slessor, Zhuang and Dimotakis2000), with the shear layer being here effectively wall bounded below its lower edge and comprising the upper layers of the recirculation. Within the context of STBLIs, the present results find the tendency to attain the symmetry level by the middle of the interaction for all cases (assumed
![]() $v_{c}=U_{b}/2$
, with inner edge near the stagnation line), with a mean shear layer convection Mach number of
$v_{c}=U_{b}/2$
, with inner edge near the stagnation line), with a mean shear layer convection Mach number of
![]() $M_{c}=1.55$
(
$M_{c}=1.55$
(
![]() ${\sim}M_{b}/2$
, where the Mach number behind the separation shock is estimated from the measured pressure rise
${\sim}M_{b}/2$
, where the Mach number behind the separation shock is estimated from the measured pressure rise
![]() $p_{p}/p_{u}$
, at the given
$p_{p}/p_{u}$
, at the given
![]() $M_{e}$
). The streamwise reduction from
$M_{e}$
). The streamwise reduction from
![]() $M_{c}=1.80$
to 1.30, hence increase in
$M_{c}=1.80$
to 1.30, hence increase in
![]() $\unicode[STIX]{x0394}M_{\unicode[STIX]{x1D719},b}$
, further suggests this tendency is not primarily determined by the process of shear layer inception upon separation (which is practically unaltered by downstream effects), but rather scales with the mean recirculation. This may be tentatively explained through comparison with the findings from Papamoschou & Bunyajitradulya (Reference Papamoschou and Bunyajitradulya1997), where fast modes with convection velocity higher than the symmetric value were observed exclusively in supersonic–subsonic shear layers (
$\unicode[STIX]{x0394}M_{\unicode[STIX]{x1D719},b}$
, further suggests this tendency is not primarily determined by the process of shear layer inception upon separation (which is practically unaltered by downstream effects), but rather scales with the mean recirculation. This may be tentatively explained through comparison with the findings from Papamoschou & Bunyajitradulya (Reference Papamoschou and Bunyajitradulya1997), where fast modes with convection velocity higher than the symmetric value were observed exclusively in supersonic–subsonic shear layers (
![]() $v_{\unicode[STIX]{x1D719}}>U_{b}/2$
up to
$v_{\unicode[STIX]{x1D719}}>U_{b}/2$
up to
![]() $X_{U}^{\ast }\approx 0.5$
in our case); slow modes were instead found only in supersonic–supersonic shear layers – here essentially as eddies enter the outer layers of the recirculation, leading to their ejection near
$X_{U}^{\ast }\approx 0.5$
in our case); slow modes were instead found only in supersonic–supersonic shear layers – here essentially as eddies enter the outer layers of the recirculation, leading to their ejection near
![]() $X_{U}^{\ast }\approx 1$
. Behind the step,
$X_{U}^{\ast }\approx 1$
. Behind the step,
![]() $v_{\unicode[STIX]{x1D719}}$
picks up at values nearly twice as high following the local expansion and then recovers towards
$v_{\unicode[STIX]{x1D719}}$
picks up at values nearly twice as high following the local expansion and then recovers towards
![]() ${\sim}U_{e}$
downstream, as generally expected for rearward-facing steps (e.g. Deepak, Gai & Neely Reference Deepak, Gai and Neely2012).
${\sim}U_{e}$
downstream, as generally expected for rearward-facing steps (e.g. Deepak, Gai & Neely Reference Deepak, Gai and Neely2012).
Following the above, the wavelength of the characteristic disturbance at the wall is estimated as
![]() $\unicode[STIX]{x1D706}_{w}=v_{\unicode[STIX]{x1D719}}/f_{ch}$
. As shown in figure 13(d), a wavelength of
$\unicode[STIX]{x1D706}_{w}=v_{\unicode[STIX]{x1D719}}/f_{ch}$
. As shown in figure 13(d), a wavelength of
![]() ${\sim}2\unicode[STIX]{x1D6FF}_{o}$
is first found near shear layer inception, and then grows monotonically as the shear layer develops downstream, attaining accordingly greater values by the ejection location for longer interactions. The aspect ratio of the near-wall disturbance upon inception (induced by local shear layer structures) is therefore approximately
${\sim}2\unicode[STIX]{x1D6FF}_{o}$
is first found near shear layer inception, and then grows monotonically as the shear layer develops downstream, attaining accordingly greater values by the ejection location for longer interactions. The aspect ratio of the near-wall disturbance upon inception (induced by local shear layer structures) is therefore approximately
![]() $\unicode[STIX]{x1D706}_{w}/\unicode[STIX]{x1D6FF}_{o}\approx 2$
; this is near the order of the scales expected for the larger eddies within the incoming turbulent boundary layer (e.g. see Brown & Thomas Reference Brown and Thomas1977, Head & Bandyopadhyay Reference Head and Bandyopadhyay1981, Smits & Dussauge Reference Smits and Dussauge2006b
).
$\unicode[STIX]{x1D706}_{w}/\unicode[STIX]{x1D6FF}_{o}\approx 2$
; this is near the order of the scales expected for the larger eddies within the incoming turbulent boundary layer (e.g. see Brown & Thomas Reference Brown and Thomas1977, Head & Bandyopadhyay Reference Head and Bandyopadhyay1981, Smits & Dussauge Reference Smits and Dussauge2006b
).
3.4 Separation bubble pulsations

Figure 14. Variation in low-frequency unsteadiness
![]() $f_{o}$
for complete range of heights: (a) upstream separation bubble, taken at
$f_{o}$
for complete range of heights: (a) upstream separation bubble, taken at
![]() $X_{U}^{\ast }=0$
(
$X_{U}^{\ast }=0$
(
![]() $S_{1}$
) and (b) downstream bubble, at
$S_{1}$
) and (b) downstream bubble, at
![]() $X_{D}^{\ast }=1$
(
$X_{D}^{\ast }=1$
(
![]() $R_{2}$
). Shown both as a function of
$R_{2}$
). Shown both as a function of
![]() $h/\unicode[STIX]{x1D6FF}_{o}$
(squares, bottom axis) and normalised mass in the bubble
$h/\unicode[STIX]{x1D6FF}_{o}$
(squares, bottom axis) and normalised mass in the bubble
![]() $M_{B}^{\ast }=M_{B}/M_{B,ref}$
(diamond symbols, top axis), where mass per unit span in the separation is estimated as
$M_{B}^{\ast }=M_{B}/M_{B,ref}$
(diamond symbols, top axis), where mass per unit span in the separation is estimated as
![]() $M_{B}=0.5\unicode[STIX]{x1D70C}_{B}Lh$
for the upstream FFS (
$M_{B}=0.5\unicode[STIX]{x1D70C}_{B}Lh$
for the upstream FFS (
![]() ${\sim}0.1\unicode[STIX]{x1D70C}_{e}$
in downstream BFS).
${\sim}0.1\unicode[STIX]{x1D70C}_{e}$
in downstream BFS).
![]() $X_{U}^{\ast }=0$
and
$X_{U}^{\ast }=0$
and
![]() $X_{D}^{\ast }=1$
locations are selected at the local
$X_{D}^{\ast }=1$
locations are selected at the local
![]() $\unicode[STIX]{x1D70E}_{p}/p$
maxima. Mass per unit span for reference highly separated case (
$\unicode[STIX]{x1D70E}_{p}/p$
maxima. Mass per unit span for reference highly separated case (
![]() $h=22.5~\text{mm}$
) is
$h=22.5~\text{mm}$
) is
![]() $M_{B,ref}=0.0004~\text{kg}~\text{m}^{-1}$
, with bubble density
$M_{B,ref}=0.0004~\text{kg}~\text{m}^{-1}$
, with bubble density
![]() $\unicode[STIX]{x1D70C}_{B}=0.31~\text{kg}~\text{m}^{-3}$
(§ 5).
$\unicode[STIX]{x1D70C}_{B}=0.31~\text{kg}~\text{m}^{-3}$
(§ 5).
Figure 14 summarises the variations in characteristic pulsation frequency
![]() $f_{o}$
for the upstream and downstream separation bubbles, with values respectively taken at
$f_{o}$
for the upstream and downstream separation bubbles, with values respectively taken at
![]() $X_{U}^{\ast }=0$
and
$X_{U}^{\ast }=0$
and
![]() $X_{D}^{\ast }=1$
. Together with the effect of step height
$X_{D}^{\ast }=1$
. Together with the effect of step height
![]() $h/\unicode[STIX]{x1D6FF}_{o}$
, both cases are further presented against the respective mass in the bubble normalised by that in the reference case
$h/\unicode[STIX]{x1D6FF}_{o}$
, both cases are further presented against the respective mass in the bubble normalised by that in the reference case
![]() $M_{B}^{\ast }=M_{B}/M_{B,ref}$
(top axis), this being taken at an azimuthal plane with mass per unit span
$M_{B}^{\ast }=M_{B}/M_{B,ref}$
(top axis), this being taken at an azimuthal plane with mass per unit span
![]() $M_{B}=0.5\unicode[STIX]{x1D70C}_{B}Lh$
and where density behind the separation shock is here
$M_{B}=0.5\unicode[STIX]{x1D70C}_{B}Lh$
and where density behind the separation shock is here
![]() $\unicode[STIX]{x1D70C}_{b}=2\unicode[STIX]{x1D70C}_{e}$
(density within the bubble
$\unicode[STIX]{x1D70C}_{b}=2\unicode[STIX]{x1D70C}_{e}$
(density within the bubble
![]() $\unicode[STIX]{x1D70C}_{B}$
scales primarily with density ratio across the shear layer
$\unicode[STIX]{x1D70C}_{B}$
scales primarily with density ratio across the shear layer
![]() $s=\unicode[STIX]{x1D70C}_{B}/\unicode[STIX]{x1D70C}_{b}$
and is effectively constant throughout the range); the density within the downstream BFS is of order
$s=\unicode[STIX]{x1D70C}_{B}/\unicode[STIX]{x1D70C}_{b}$
and is effectively constant throughout the range); the density within the downstream BFS is of order
![]() ${\sim}0.1\unicode[STIX]{x1D70C}_{e}$
. Note the
${\sim}0.1\unicode[STIX]{x1D70C}_{e}$
. Note the
![]() $f_{o}$
variations with
$f_{o}$
variations with
![]() $M_{B}^{\ast }$
are subsequently investigated in further detail through assessment of the bubble breathing dynamics, in § 5. As per figure 14(a), the low-frequency unsteadiness in the upstream FFS drops significantly with increasing step height, particularly for shorter steps as the dominant frequency of 1872 Hz for
$M_{B}^{\ast }$
are subsequently investigated in further detail through assessment of the bubble breathing dynamics, in § 5. As per figure 14(a), the low-frequency unsteadiness in the upstream FFS drops significantly with increasing step height, particularly for shorter steps as the dominant frequency of 1872 Hz for
![]() $h/\unicode[STIX]{x1D6FF}_{o}=0.3$
(
$h/\unicode[STIX]{x1D6FF}_{o}=0.3$
(
![]() $M_{B}^{\ast }=7\times 10^{-3}$
) decreases rapidly down to 1250 Hz by
$M_{B}^{\ast }=7\times 10^{-3}$
) decreases rapidly down to 1250 Hz by
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
(
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
(
![]() $M_{B}^{\ast }=5.4\times 10^{-2}$
). Thereafter,
$M_{B}^{\ast }=5.4\times 10^{-2}$
). Thereafter,
![]() $f_{o}$
is found to decrease gradually all the way down to 391 Hz, involving
$f_{o}$
is found to decrease gradually all the way down to 391 Hz, involving
![]() $M_{B}^{\ast }$
variations of two orders of magnitude as a whole. In the downstream BFS (figure 14
b),
$M_{B}^{\ast }$
variations of two orders of magnitude as a whole. In the downstream BFS (figure 14
b),
![]() $f_{o}$
drops from 19.70 kHz to 9.27 kHz between the
$f_{o}$
drops from 19.70 kHz to 9.27 kHz between the
![]() $h/\unicode[STIX]{x1D6FF}_{o}=0.3$
and
$h/\unicode[STIX]{x1D6FF}_{o}=0.3$
and
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
cases. For taller steps, the frequency at reattachment is found at about 5.5 kHz (cf. gradual drop in
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
cases. For taller steps, the frequency at reattachment is found at about 5.5 kHz (cf. gradual drop in
![]() $f_{o}$
in the upstream separation), attaining a minimum value of 3.55 kHz for the reference case.
$f_{o}$
in the upstream separation), attaining a minimum value of 3.55 kHz for the reference case.
Overall, the shear layer’s effect thus proves particularly critical when the scale of separation is sufficiently large to enable the onset of instabilities, which in turn evolve in the form of coherent eddies along the interaction. In the following, the highly separated case is further investigated at different flow conditions.
4 Separated shear layer characterisation
4.1 Effect of Mach number
Tests were subsequently conducted at Mach 2.0 and 3.0, with the two 22.5 mm-step cases corresponding to a
![]() $h/\unicode[STIX]{x1D6FF}_{o}=7.0$
ratio (at
$h/\unicode[STIX]{x1D6FF}_{o}=7.0$
ratio (at
![]() $M_{e}=3.0$
,
$M_{e}=3.0$
,
![]() $Re_{e}/m=6.1\times 10^{7}$
) and
$Re_{e}/m=6.1\times 10^{7}$
) and
![]() $h/\unicode[STIX]{x1D6FF}_{o}=8.0$
(at
$h/\unicode[STIX]{x1D6FF}_{o}=8.0$
(at
![]() $M_{e}=2.0$
,
$M_{e}=2.0$
,
![]() $Re_{e}/m=6.5\times 10^{7}$
). The boundary layer is again fully turbulent and at a similar unit Reynolds number as in the Mach 3.9 tests (see table 1). For the characterisation of the shear layer’s effect, the analysis hereafter in the paper is centred around the FFS interaction; nomenclature from here on refers solely to the upstream separation.
$Re_{e}/m=6.5\times 10^{7}$
). The boundary layer is again fully turbulent and at a similar unit Reynolds number as in the Mach 3.9 tests (see table 1). For the characterisation of the shear layer’s effect, the analysis hereafter in the paper is centred around the FFS interaction; nomenclature from here on refers solely to the upstream separation.

Figure 15. Mach number effect: (a) mean pressure for
![]() $M_{e}=2.0$
(
$M_{e}=2.0$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=8.0$
),
$h/\unicode[STIX]{x1D6FF}_{o}=8.0$
),
![]() $M_{e}=3.0~(h/\unicode[STIX]{x1D6FF}_{o}=7.0)$
and
$M_{e}=3.0~(h/\unicode[STIX]{x1D6FF}_{o}=7.0)$
and
![]() $M_{e}=3.9$
(
$M_{e}=3.9$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
) FFS interactions, all with tallest step height of
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
) FFS interactions, all with tallest step height of
![]() $h=22.5~\text{mm}$
; and (b) respective schlieren images. Reynolds number kept at
$h=22.5~\text{mm}$
; and (b) respective schlieren images. Reynolds number kept at
![]() $Re_{e}/m=6.1\times 10^{7}$
(
$Re_{e}/m=6.1\times 10^{7}$
(
![]() $^{\ast }6.5\times 10^{7}$
at
$^{\ast }6.5\times 10^{7}$
at
![]() $M_{e}=2.0$
), flow conditions as per table 3. Reference pressure is
$M_{e}=2.0$
), flow conditions as per table 3. Reference pressure is
![]() $p_{u}=9.84$
, 23.26 and 68.37 kPa from higher to lower Mach number (at reference
$p_{u}=9.84$
, 23.26 and 68.37 kPa from higher to lower Mach number (at reference
![]() $S_{1}$
location, no step in the model). Supplementary schlieren movies covering the complete axisymmetric step region are available at https://doi.org/10.1017/jfm.2018.350 as movie 1.
$S_{1}$
location, no step in the model). Supplementary schlieren movies covering the complete axisymmetric step region are available at https://doi.org/10.1017/jfm.2018.350 as movie 1.

Figure 16. Comparison of present
![]() $M_{e}=2.0$
, 3.0 and 3.9 FFS interactions (
$M_{e}=2.0$
, 3.0 and 3.9 FFS interactions (
![]() $h=22.5~\text{mm}$
) with other STBLIs with separation in the literature: (a) separation length with respect to obstacle height
$h=22.5~\text{mm}$
) with other STBLIs with separation in the literature: (a) separation length with respect to obstacle height
![]() $L/h$
for different high deflection corner and step configurations
$L/h$
for different high deflection corner and step configurations
![]() $\unicode[STIX]{x1D6FC}$
(surface deflection angle, see schematic) and (b) plateau to reference pressure levels
$\unicode[STIX]{x1D6FC}$
(surface deflection angle, see schematic) and (b) plateau to reference pressure levels
![]() $p_{p}/p_{u}$
for different Mach number conditions. Adding similar correlations in Knight & Zheltovodov (Reference Knight, Zheltovodov, Babinsky and Harvey2014) and including present dataset as well as finite span ramp cases in Estruch-Samper (Reference Estruch-Samper2016) (Mach 8.2,
$p_{p}/p_{u}$
for different Mach number conditions. Adding similar correlations in Knight & Zheltovodov (Reference Knight, Zheltovodov, Babinsky and Harvey2014) and including present dataset as well as finite span ramp cases in Estruch-Samper (Reference Estruch-Samper2016) (Mach 8.2,
![]() $\ast$
symbols).
$\ast$
symbols).

Figure 17. Pressure PSD within separation region of
![]() $M_{e}=2.0$
(left column) and
$M_{e}=2.0$
(left column) and
![]() $M_{e}=3.0$
(right column) FFS interactions: (a,b) PSD plots, and (c,d) respective contours in the (f,x)-plane. Both at similar Reynolds number and corresponding to cases in figure 15 (refer to caption).
$M_{e}=3.0$
(right column) FFS interactions: (a,b) PSD plots, and (c,d) respective contours in the (f,x)-plane. Both at similar Reynolds number and corresponding to cases in figure 15 (refer to caption).

Figure 18. Reynolds number effect: (a) mean pressure for
![]() $Re_{e}/m=2.7\times 10^{7}$
(
$Re_{e}/m=2.7\times 10^{7}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=6.4$
),
$h/\unicode[STIX]{x1D6FF}_{o}=6.4$
),
![]() $Re_{e}/m=6.1\times 10^{7}$
(
$Re_{e}/m=6.1\times 10^{7}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=7.0$
) and
$h/\unicode[STIX]{x1D6FF}_{o}=7.0$
) and
![]() $Re_{e}/m=8.4\times 10^{7}$
(
$Re_{e}/m=8.4\times 10^{7}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=7.3$
) FFS interactions, for a step height of
$h/\unicode[STIX]{x1D6FF}_{o}=7.3$
) FFS interactions, for a step height of
![]() $h=22.5~\text{mm}$
; with (b) respective schlieren images. Mach number kept constant at
$h=22.5~\text{mm}$
; with (b) respective schlieren images. Mach number kept constant at
![]() $M_{e}=3.0$
; flow conditions as per table 3. Reference pressure is
$M_{e}=3.0$
; flow conditions as per table 3. Reference pressure is
![]() $p_{u}=10.20$
, 23.26 and 32.18 kPa from lower to higher Reynolds number (at reference
$p_{u}=10.20$
, 23.26 and 32.18 kPa from lower to higher Reynolds number (at reference
![]() $S_{1}$
location, no step in the model).
$S_{1}$
location, no step in the model).
As shown in the mean pressure measurements and schlieren in figure 15, the separation length is relatively shorter than that for the reference Mach 3.9 case (figure 8), respectively
![]() $L=87.75~\text{mm}$
at Mach 2.0 and
$L=87.75~\text{mm}$
at Mach 2.0 and
![]() $L=96.75~\text{mm}$
at Mach 3.0; with boundary-layer thickness down to
$L=96.75~\text{mm}$
at Mach 3.0; with boundary-layer thickness down to
![]() $\unicode[STIX]{x1D6FF}_{o}=2.8~\text{mm}$
and 3.2 mm at these lower Mach numbers. The pressure trends are similar to those in figure 6(a) and separation length scales at a practically constant
$\unicode[STIX]{x1D6FF}_{o}=2.8~\text{mm}$
and 3.2 mm at these lower Mach numbers. The pressure trends are similar to those in figure 6(a) and separation length scales at a practically constant
![]() $L/\unicode[STIX]{x1D6FF}_{o}\approx 30$
for this step height. The separation aspect ratios are
$L/\unicode[STIX]{x1D6FF}_{o}\approx 30$
for this step height. The separation aspect ratios are
![]() $L/h=3.9$
and 4.3 (cf.
$L/h=3.9$
and 4.3 (cf.
![]() $L/h=5.1$
for Mach 3.9), falling within the range reported across past studies – see figure 16(a), where this is evaluated for different Mach numbers and ramp deflection angles
$L/h=5.1$
for Mach 3.9), falling within the range reported across past studies – see figure 16(a), where this is evaluated for different Mach numbers and ramp deflection angles
![]() $\unicode[STIX]{x1D6FC}$
(see Knight & Zheltovodov (Reference Knight, Zheltovodov, Babinsky and Harvey2014) for details on the reference cases in the plot). As shown in figure 16(b), the pressure ratio across separation is primarily a function of the Mach number and finds close agreement with the simple empirical correlation
$\unicode[STIX]{x1D6FC}$
(see Knight & Zheltovodov (Reference Knight, Zheltovodov, Babinsky and Harvey2014) for details on the reference cases in the plot). As shown in figure 16(b), the pressure ratio across separation is primarily a function of the Mach number and finds close agreement with the simple empirical correlation
![]() $p_{p}/p_{u}=0.5M_{e}+1$
, as given in the latter reference as well (
$p_{p}/p_{u}=0.5M_{e}+1$
, as given in the latter reference as well (
![]() $p_{u}\approx p_{\infty }$
and
$p_{u}\approx p_{\infty }$
and
![]() $M_{e}\approx M_{\infty }$
for flat plate cases).
$M_{e}\approx M_{\infty }$
for flat plate cases).
The spectra in figure 17(a,b) again reflect the narrowband low-frequency unsteadiness at separation (
![]() $X^{\ast }=0$
), together with a predominant shear layer influence over the recirculation length. For the Mach 2.0 case, further instabilities appear to develop within the separation region, partly attributed to the formation of secondary recirculations (embedded within the bubble), yet with the dominant influence of the separated shear layer with origin close behind
$X^{\ast }=0$
), together with a predominant shear layer influence over the recirculation length. For the Mach 2.0 case, further instabilities appear to develop within the separation region, partly attributed to the formation of secondary recirculations (embedded within the bubble), yet with the dominant influence of the separated shear layer with origin close behind
![]() $X^{\ast }=0$
remaining clearly defined in the contours (figure 17
c,d). The trend overall resembles that obtained at Mach 3.9, with a higher spreading angle in the Mach 2.0 interaction – where the mean shear layer convection velocity falls just within the low-transonic regime, a convection Mach number of
$X^{\ast }=0$
remaining clearly defined in the contours (figure 17
c,d). The trend overall resembles that obtained at Mach 3.9, with a higher spreading angle in the Mach 2.0 interaction – where the mean shear layer convection velocity falls just within the low-transonic regime, a convection Mach number of
![]() $M_{c}\approx 0.8$
(whereby
$M_{c}\approx 0.8$
(whereby
![]() $M_{b}=1.6$
). The Mach 3.0 interaction, with
$M_{b}=1.6$
). The Mach 3.0 interaction, with
![]() $M_{c}\approx 1.25$
(
$M_{c}\approx 1.25$
(
![]() $M_{b}=2.5$
), instead exhibits a similar development as that in the earlier cases and may be seen to represent an effective threshold above which shear layer growth remains practically invariant with further increases in
$M_{b}=2.5$
), instead exhibits a similar development as that in the earlier cases and may be seen to represent an effective threshold above which shear layer growth remains practically invariant with further increases in
![]() $M_{c}$
. As such, it is noted that many of the reference cases in table 2 would fall within
$M_{c}$
. As such, it is noted that many of the reference cases in table 2 would fall within
![]() $M_{c}\approx 0.75$
–1.25, where such variations would likely be significant.
$M_{c}\approx 0.75$
–1.25, where such variations would likely be significant.
Table 3. Nominal flow conditions for study on Reynolds number effect.

4.2 Effect of Reynolds number
Later tests then looked into the effect of Reynolds number for the same configuration (
![]() $h=22.5~\text{mm}$
step). Given the wider
$h=22.5~\text{mm}$
step). Given the wider
![]() $P_{o,\infty }$
range in the facility, experiments were conducted at Mach 3.0, respectively at lower and higher Reynolds numbers of
$P_{o,\infty }$
range in the facility, experiments were conducted at Mach 3.0, respectively at lower and higher Reynolds numbers of
![]() $Re_{e}/m=2.7\times 10^{7}$
and
$Re_{e}/m=2.7\times 10^{7}$
and
![]() $8.4\times 10^{7}$
(
$8.4\times 10^{7}$
(
![]() $h/\unicode[STIX]{x1D6FF}_{o}=6.4$
and 7.3, as per table 3).
$h/\unicode[STIX]{x1D6FF}_{o}=6.4$
and 7.3, as per table 3).

Figure 19. Pressure PSD within separation region of
![]() $Re_{e}/m=2.7\times 10^{7}$
(left column) and
$Re_{e}/m=2.7\times 10^{7}$
(left column) and
![]() $Re_{e}/m=8.4\times 10^{7}$
(right column) FFS interactions: (a,b) PSD plots, and (c,d) respective contours in the (f, x)-plane, both at
$Re_{e}/m=8.4\times 10^{7}$
(right column) FFS interactions: (a,b) PSD plots, and (c,d) respective contours in the (f, x)-plane, both at
![]() $M_{e}=3.0$
. Corresponding to cases in figure 18.
$M_{e}=3.0$
. Corresponding to cases in figure 18.
The mean pressure trends and schlieren images are shown in figure 18, with the shear layer again evidenced in the latter. As such, the unsteadiness along the plateau region is similarly dominated by the high- to mid-frequency instabilities associated with shear layer shedding (figure 19
a,b). The mean organisation of the separated flow intrinsically varies as a function of Reynolds number, which is in part expected to dominate the formation of secondary recirculations, or more – this being of an inherently complex nature itself (e.g. see Delery & Marvin Reference Delery and Marvin1986). For the higher Reynolds number case, the evolution of the shear layer spectra appears disturbed closer to the step, due to the localised corner effects. In the contours (figure 19
c,d), the shift to lower frequencies is once again evidenced across the axial length, with inherent variations in fluctuation intensity. As similarly noted in Souverein et al. (Reference Souverein, Dupont, Debiève, Dussauge, Van Oudheusden and Scarano2010), the global properties of the interaction thus remain practically unaffected across substantial variations in Reynolds number and may overall exhibit a large resemblance in the turbulent field – where here the separated shear layer is found to maintain its dominant influence with its footprint remaining clearly defined throughout the dataset (down to
![]() $Re_{\unicode[STIX]{x1D6FF}}\approx 10^{5}$
for the lower Reynolds number case). This renders the shear layer primarily sensitive to Mach number, with its growth being gradually inhibited with increasing
$Re_{\unicode[STIX]{x1D6FF}}\approx 10^{5}$
for the lower Reynolds number case). This renders the shear layer primarily sensitive to Mach number, with its growth being gradually inhibited with increasing
![]() $M_{c}$
– up to a certain threshold, here for
$M_{c}$
– up to a certain threshold, here for
![]() $M_{e}\geqslant 3.0$
(whereby
$M_{e}\geqslant 3.0$
(whereby
![]() $M_{c}\geqslant 1.25$
).
$M_{c}\geqslant 1.25$
).

Figure 20. Pressure contours in
![]() $(t,x)$
-plane over
$(t,x)$
-plane over
![]() $20T_{o}$
-long sample periods with close up into
$20T_{o}$
-long sample periods with close up into
![]() $5T_{o}$
-window and corresponding signals for the highly separated cases (
$5T_{o}$
-window and corresponding signals for the highly separated cases (
![]() $h=22.5~\text{mm}$
step) at: (a)
$h=22.5~\text{mm}$
step) at: (a)
![]() $M_{e}=3.9$
,
$M_{e}=3.9$
,
![]() $Re_{e}/m=6.1\times 10^{7}$
; (b)
$Re_{e}/m=6.1\times 10^{7}$
; (b)
![]() $M_{e}=3.0$
,
$M_{e}=3.0$
,
![]() $Re_{e}/m=8.4\times 10^{7}$
; (c)
$Re_{e}/m=8.4\times 10^{7}$
; (c)
![]() $M_{e}=3.0$
,
$M_{e}=3.0$
,
![]() $Re_{e}/m=6.1\times 10^{7}$
; (d)
$Re_{e}/m=6.1\times 10^{7}$
; (d)
![]() $M_{e}=3.0$
,
$M_{e}=3.0$
,
![]() $Re_{e}/m=2.7\times 10^{7}$
and (e)
$Re_{e}/m=2.7\times 10^{7}$
and (e)
![]() $M_{e}=2.0$
,
$M_{e}=2.0$
,
![]() $Re_{e}/m=6.5\times 10^{7}$
. Red dashed line indicates separation location
$Re_{e}/m=6.5\times 10^{7}$
. Red dashed line indicates separation location
![]() $x_{o}=0$
and black dashed line is taken at
$x_{o}=0$
and black dashed line is taken at
![]() $5\unicode[STIX]{x1D6FF}_{o}$
downstream (near inception). Characteristic time scales of bubble pulsation
$5\unicode[STIX]{x1D6FF}_{o}$
downstream (near inception). Characteristic time scales of bubble pulsation
![]() $T_{o}$
(
$T_{o}$
(
![]() $f_{o}^{-1}$
) and reference
$f_{o}^{-1}$
) and reference
![]() $\unicode[STIX]{x1D6FF}_{o}$
for each case as listed in table 2. Ejection location
$\unicode[STIX]{x1D6FF}_{o}$
for each case as listed in table 2. Ejection location
![]() $x_{ej}$
taken at measurement station just ahead of the step,
$x_{ej}$
taken at measurement station just ahead of the step,
![]() $X_{ej}^{\ast }=0.98$
.
$X_{ej}^{\ast }=0.98$
.
4.3 Low-frequency decay–growth cycle
The pressure PSDs at separation (
![]() $X^{\ast }=0$
) thus overall exhibit a clear dominance of the low-frequency pulsations as a single ‘global’ mode
$X^{\ast }=0$
) thus overall exhibit a clear dominance of the low-frequency pulsations as a single ‘global’ mode
![]() $f_{o}$
, associated with the bubble’s decay–growth cycle. To further illustrate the process, samples of the pressure contours over the
$f_{o}$
, associated with the bubble’s decay–growth cycle. To further illustrate the process, samples of the pressure contours over the
![]() $(t,x)$
-plane and representative of the highly separated cases are presented in figure 20, with time normalised by the characteristic time scale of bubble breathing
$(t,x)$
-plane and representative of the highly separated cases are presented in figure 20, with time normalised by the characteristic time scale of bubble breathing
![]() $t/T_{o}$
(see the corresponding
$t/T_{o}$
(see the corresponding
![]() $f_{o}$
in table 2). Contours covering the complete FFS region over a sample duration of
$f_{o}$
in table 2). Contours covering the complete FFS region over a sample duration of
![]() $20T_{o}$
evidence the large-scale pulsations near separation, with the respective signals shown on the right (note spectral analysis covers a total
$20T_{o}$
evidence the large-scale pulsations near separation, with the respective signals shown on the right (note spectral analysis covers a total
![]() $2000T_{o}$
–
$2000T_{o}$
–
![]() $10\,000T_{o}$
across the complete dataset, yielding a more precise statistical measure). A look into selected
$10\,000T_{o}$
across the complete dataset, yielding a more precise statistical measure). A look into selected
![]() $5T_{o}$
windows offers a close-up view into the region near separation and early shear layer development, evidencing in further detail the occasional bursts and relatively quiescent stages that appear (rather arbitrarily) over the broadly periodic pulsations. Within the observed irregularities – in part also attributed to small-scale turbulence and shear/dissipation effects – the shear layer is thus remarked to be inherently subjected to large-scale motions over the cycle.
$5T_{o}$
windows offers a close-up view into the region near separation and early shear layer development, evidencing in further detail the occasional bursts and relatively quiescent stages that appear (rather arbitrarily) over the broadly periodic pulsations. Within the observed irregularities – in part also attributed to small-scale turbulence and shear/dissipation effects – the shear layer is thus remarked to be inherently subjected to large-scale motions over the cycle.

Figure 21. Simplified schematic of a characteristic sequence of low-frequency pulsation including: bubble shrinking (
![]() $0\lesssim t\lesssim 0.25T_{o}$
), recharge towards mean (
$0\lesssim t\lesssim 0.25T_{o}$
), recharge towards mean (
![]() $0.25T_{o}\lesssim t\lesssim 0.5T_{o}$
), further expansion of the bubble (
$0.25T_{o}\lesssim t\lesssim 0.5T_{o}$
), further expansion of the bubble (
![]() $0.5T_{o}\lesssim t\lesssim 0.75T_{o}$
) and collapse back to mean state (
$0.5T_{o}\lesssim t\lesssim 0.75T_{o}$
) and collapse back to mean state (
![]() $0.75T_{o}\lesssim t\lesssim T_{o}$
). Schematic not to scale and only representative of ‘characteristic’ contraction–expansion cycle over long periods. Arrows indicate out-of-phase motions between the separation and reattachment shocks, with input mass flow rate
$0.75T_{o}\lesssim t\lesssim T_{o}$
). Schematic not to scale and only representative of ‘characteristic’ contraction–expansion cycle over long periods. Arrows indicate out-of-phase motions between the separation and reattachment shocks, with input mass flow rate
![]() ${\dot{m}}_{in}$
(at recharge) and mass ejection rate
${\dot{m}}_{in}$
(at recharge) and mass ejection rate
![]() ${\dot{m}}_{ej}$
near
${\dot{m}}_{ej}$
near
![]() $X_{ej}^{\ast }\approx 1$
(depletion).
$X_{ej}^{\ast }\approx 1$
(depletion).
Figure 21 represents a characteristic pulsation of the bubble, assuming constant shock velocity and equidistant upstream/downstream displacements, at an estimated
![]() $\pm 2\,\%U_{b}$
(up to
$\pm 2\,\%U_{b}$
(up to
![]() $\pm 4\,\%U_{b}$
for
$\pm 4\,\%U_{b}$
for
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
). As earlier noted, the separation and reattachment shocks oscillate out of phase, with displacements of the latter rapidly succeeding separation-shock motions. The schematic here represents a characteristic pulsation, with times only indicative and where
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
). As earlier noted, the separation and reattachment shocks oscillate out of phase, with displacements of the latter rapidly succeeding separation-shock motions. The schematic here represents a characteristic pulsation, with times only indicative and where
![]() $t/T_{o}=0$
is taken at the mean separation location (
$t/T_{o}=0$
is taken at the mean separation location (
![]() $S_{1}$
at
$S_{1}$
at
![]() $X^{\ast }\approx 0$
). Large-scale shear layer structures, whilst pseudoperiodic in nature, are represented as series of eddies which effectively manifest as trains of turbulent events convecting intermittently along the separation. At
$X^{\ast }\approx 0$
). Large-scale shear layer structures, whilst pseudoperiodic in nature, are represented as series of eddies which effectively manifest as trains of turbulent events convecting intermittently along the separation. At
![]() ${\sim}0.25T_{o}$
into the cycle, the bubble is shown to have contracted, having lost part of its initial mass through eddy entrainment and approaching incipient separation conditions by this stage; a refill mechanism, initiated with the upstream shift of the separation shock, then leads to an influx of flow into the bubble to recover the depleted mass; this would be effectively driven via reattachment, as the incoming separated flow enters the recirculation (
${\sim}0.25T_{o}$
into the cycle, the bubble is shown to have contracted, having lost part of its initial mass through eddy entrainment and approaching incipient separation conditions by this stage; a refill mechanism, initiated with the upstream shift of the separation shock, then leads to an influx of flow into the bubble to recover the depleted mass; this would be effectively driven via reattachment, as the incoming separated flow enters the recirculation (
![]() ${\dot{m}}_{in}$
). During its recharge, the bubble then expands through
${\dot{m}}_{in}$
). During its recharge, the bubble then expands through
![]() $0.5T_{o}$
and towards its most dilated state at about 0.75
$0.5T_{o}$
and towards its most dilated state at about 0.75
![]() $T_{o}$
. As the separation then shifts farther upstream, a longer shear layer path is in turn enabled and, by the end of the cycle
$T_{o}$
. As the separation then shifts farther upstream, a longer shear layer path is in turn enabled and, by the end of the cycle
![]() $t=T_{o}$
, it then returns to its original (mean) state, with separated mass
$t=T_{o}$
, it then returns to its original (mean) state, with separated mass
![]() ${\sim}M_{B}$
.
${\sim}M_{B}$
.
The separation is thus drained across the sequence as a result of the cumulative entrainment by shear layer eddies, which progressively feed from their surrounding flow all the way down to their ejection. The bubble is in turn repetitively recharged to preserve its mass, leading to its growth–decay dynamics. The nature of this low-frequency mechanism is explored in further detail next.

Figure 22. Present dataset (symbols as in figures 15 and 18): (a) variation in mean separated mass per unit span
![]() $M_{B}^{\ast }$
(
$M_{B}^{\ast }$
(
![]() $=M_{B}/M_{B,ref}$
where
$=M_{B}/M_{B,ref}$
where
![]() $M_{B,ref}=0.0004~\text{kg}~\text{m}^{-1}$
for reference case, see figure 14
a) and (b) normalised low-frequency unsteadiness as
$M_{B,ref}=0.0004~\text{kg}~\text{m}^{-1}$
for reference case, see figure 14
a) and (b) normalised low-frequency unsteadiness as
![]() $St_{o,L}$
versus
$St_{o,L}$
versus
![]() $M_{e}$
, compared with the studies in table 2 (see symbols). Velocity behind separation shock is
$M_{e}$
, compared with the studies in table 2 (see symbols). Velocity behind separation shock is
![]() $U_{b}=458~\text{m}~\text{s}^{-1}$
for
$U_{b}=458~\text{m}~\text{s}^{-1}$
for
![]() $M_{e}=2.0$
(
$M_{e}=2.0$
(
![]() $M_{b}=1.6$
),
$M_{b}=1.6$
),
![]() $575~\text{m}~\text{s}^{-1}$
for
$575~\text{m}~\text{s}^{-1}$
for
![]() $M_{e}=3.0$
(
$M_{e}=3.0$
(
![]() $M_{b}=2.5$
) and
$M_{b}=2.5$
) and
![]() $638~\text{m}~\text{s}^{-1}$
for
$638~\text{m}~\text{s}^{-1}$
for
![]() $M_{e}=3.9$
(
$M_{e}=3.9$
(
![]() $M_{b}=3.1$
). Density within the bubble is based on adiabatic assumptions across the shear layer and taken as:
$M_{b}=3.1$
). Density within the bubble is based on adiabatic assumptions across the shear layer and taken as:
![]() $\unicode[STIX]{x1D70C}_{B}=1.62~\text{kg}~\text{m}^{3}$
,
$\unicode[STIX]{x1D70C}_{B}=1.62~\text{kg}~\text{m}^{3}$
,
![]() $0.66~\text{kg}~\text{m}^{-3}$
and
$0.66~\text{kg}~\text{m}^{-3}$
and
![]() $0.31~\text{kg}~\text{m}^{-3}$
(from
$0.31~\text{kg}~\text{m}^{-3}$
(from
![]() $M_{e}=2.0$
to
$M_{e}=2.0$
to
![]() $M_{e}=3.9$
,
$M_{e}=3.9$
,
![]() $Re_{e}/m=6.1\times 10^{7}$
, with the density ratio accordingly
$Re_{e}/m=6.1\times 10^{7}$
, with the density ratio accordingly
![]() $s\approx 0.70$
, 0.48 and 0.34);
$s\approx 0.70$
, 0.48 and 0.34);
![]() $\unicode[STIX]{x1D70C}_{B}=0.29~\text{kg}~\text{m}^{-3}$
(
$\unicode[STIX]{x1D70C}_{B}=0.29~\text{kg}~\text{m}^{-3}$
(
![]() $M_{e}=3.0$
,
$M_{e}=3.0$
,
![]() $Re_{e}/m=2.7\times 10^{7}$
) and
$Re_{e}/m=2.7\times 10^{7}$
) and
![]() $0.92~\text{kg}~\text{m}^{-3}$
(
$0.92~\text{kg}~\text{m}^{-3}$
(
![]() $M_{e}=3.0$
,
$M_{e}=3.0$
,
![]() $Re_{e}/m=8.4\times 10^{7}$
), both with
$Re_{e}/m=8.4\times 10^{7}$
), both with
![]() $s\approx 0.48$
. Dashed lines delimit cases within
$s\approx 0.48$
. Dashed lines delimit cases within
![]() $1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
Mach 3.9 range, reference
$1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
Mach 3.9 range, reference
![]() $h/\unicode[STIX]{x1D6FF}_{o}=5.9$
case indicated as dark square.
$h/\unicode[STIX]{x1D6FF}_{o}=5.9$
case indicated as dark square.
5 Interaction low-frequency unsteadiness
5.1 Separated mass variations
The analysis hereafter goes on to evaluate the mechanism of bubble breathing across the range of separated mass variations in the dataset. As shown in figure 22(a), the mass within the bubble scales roughly as the square of separation length
![]() $M_{B}\propto L^{2}$
over the Mach 3.9 range (as per § 3, and since
$M_{B}\propto L^{2}$
over the Mach 3.9 range (as per § 3, and since
![]() $L\propto h$
), with the values for the highly separated interactions at different flow conditions (§ 4) accordingly falling in the upper range of the plot. The density within the bubble is here estimated through adiabatic assumptions, based on the associated density ratio across the shear layer
$L\propto h$
), with the values for the highly separated interactions at different flow conditions (§ 4) accordingly falling in the upper range of the plot. The density within the bubble is here estimated through adiabatic assumptions, based on the associated density ratio across the shear layer
![]() $s=\unicode[STIX]{x1D70C}_{B}/\unicode[STIX]{x1D70C}_{b}$
(taking the inner bound at
$s=\unicode[STIX]{x1D70C}_{B}/\unicode[STIX]{x1D70C}_{b}$
(taking the inner bound at
![]() $M\approx 0.05$
).
$M\approx 0.05$
).
Figure 22(b) presents the low-frequency unsteadiness in terms of
![]() $St_{o,L}$
together with the reference cases in table 2, finding relatively wide variations and a particularly large spread among the reference compression corner cases. Similar scalings in terms of
$St_{o,L}$
together with the reference cases in table 2, finding relatively wide variations and a particularly large spread among the reference compression corner cases. Similar scalings in terms of
![]() $St_{o,\unicode[STIX]{x1D6FF}}$
and
$St_{o,\unicode[STIX]{x1D6FF}}$
and
![]() $St_{o,Li}$
were noted to exhibit significant variations as well, with the latter term proving slightly more successful and finding a good number of studies to fall within
$St_{o,Li}$
were noted to exhibit significant variations as well, with the latter term proving slightly more successful and finding a good number of studies to fall within
![]() $0.014\pm 0.004$
. As earlier noted, the present cases range between
$0.014\pm 0.004$
. As earlier noted, the present cases range between
![]() $L_{i}/\unicode[STIX]{x1D6FF}_{o}=2.4$
and 4.5 at Mach 3.9 (from
$L_{i}/\unicode[STIX]{x1D6FF}_{o}=2.4$
and 4.5 at Mach 3.9 (from
![]() $h/\unicode[STIX]{x1D6FF}_{o}=1.0$
to 5.9), with
$h/\unicode[STIX]{x1D6FF}_{o}=1.0$
to 5.9), with
![]() $L_{i}/\unicode[STIX]{x1D6FF}_{o}=5.1$
–6.0 for the Mach 2.0 and 3.0 interactions (see table 2) – i.e. the shock foot undergoes larger-scale motions, at lower shock velocity
$L_{i}/\unicode[STIX]{x1D6FF}_{o}=5.1$
–6.0 for the Mach 2.0 and 3.0 interactions (see table 2) – i.e. the shock foot undergoes larger-scale motions, at lower shock velocity
![]() $v_{S}$
, as the scale of separation increases. Further assessments based on the shear layer scalings in Piponniau et al. (Reference Piponniau, Dussauge, Debiève and Dupont2009) – accounting for variations as a function of
$v_{S}$
, as the scale of separation increases. Further assessments based on the shear layer scalings in Piponniau et al. (Reference Piponniau, Dussauge, Debiève and Dupont2009) – accounting for variations as a function of
![]() $M_{c}$
and sensitivities to the velocity and density ratios across it – also noted relatively improved collapse for interactions with fully developed separation (for
$M_{c}$
and sensitivities to the velocity and density ratios across it – also noted relatively improved collapse for interactions with fully developed separation (for
![]() $h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
here), overall pointing at an influence of the shear layer on interaction unsteadiness.
$h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
here), overall pointing at an influence of the shear layer on interaction unsteadiness.
5.2 Scaling of the shear layer effect
The shear layer’s evolution is next evaluated for the different flow conditions, first shown for the highly separated cases (
![]() $L/\unicode[STIX]{x1D6FF}_{o}\approx 30$
,
$L/\unicode[STIX]{x1D6FF}_{o}\approx 30$
,
![]() $h=22.5~\text{mm}$
). As per Dupont et al. (Reference Dupont, Haddad and Debiève2006), this may be assessed through a mixing layer scaling in the form:
$h=22.5~\text{mm}$
). As per Dupont et al. (Reference Dupont, Haddad and Debiève2006), this may be assessed through a mixing layer scaling in the form:
where
![]() $S_{tr}=f\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}/U_{c}$
is the classical Strouhal number for a mixing layer, with thickness
$S_{tr}=f\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}/U_{c}$
is the classical Strouhal number for a mixing layer, with thickness
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D6FF}^{\prime }X$
and spreading rate
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D6FF}^{\prime }X$
and spreading rate
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
. This is then shown normalised as
$\unicode[STIX]{x1D6FF}^{\prime }$
. This is then shown normalised as
![]() $St_{L}^{-1}$
over
$St_{L}^{-1}$
over
![]() $X^{\ast }$
to evaluate streamwise evolution.
$X^{\ast }$
to evaluate streamwise evolution.

Figure 23. Streamwise evolution of shear layer instability along upstream separation for large-scale interactions (
![]() $h=22.5~\text{mm}$
) at varying flow conditions: (a) with inverse of Strouhal number based on separation length
$h=22.5~\text{mm}$
) at varying flow conditions: (a) with inverse of Strouhal number based on separation length
![]() $St_{L}^{-1}$
and as a function of
$St_{L}^{-1}$
and as a function of
![]() $X^{\ast }$
, and (b) based on reference boundary-layer thickness,
$X^{\ast }$
, and (b) based on reference boundary-layer thickness,
![]() $St_{\unicode[STIX]{x1D6FF}}^{-1}$
versus
$St_{\unicode[STIX]{x1D6FF}}^{-1}$
versus
![]() $X^{\ast }$
. *Supersedes reference to
$X^{\ast }$
. *Supersedes reference to
![]() $St_{\unicode[STIX]{x1D703}}^{-1}$
in Chandola et al. (Reference Chandola, Huang and Estruch-Samper2017).
$St_{\unicode[STIX]{x1D703}}^{-1}$
in Chandola et al. (Reference Chandola, Huang and Estruch-Samper2017).
In figure 23, the respective tendencies are found to be effectively linear, with progressive slope variations across the range. Two further STBLI studies to have documented an evolution of shear layer instabilities, earlier highlighted in table 2, are included for comparison: the Mach 1.5 compression corner interaction in Thomas et al. is found to follow a similar trend, slightly offset (
![]() $L/\unicode[STIX]{x1D6FF}_{o}=2.1$
,
$L/\unicode[STIX]{x1D6FF}_{o}=2.1$
,
![]() $M_{b}=0.96$
), while the strongest Mach 2.3 incident shock interaction in Dupont et al. instead falls at a higher
$M_{b}=0.96$
), while the strongest Mach 2.3 incident shock interaction in Dupont et al. instead falls at a higher
![]() $St_{L}^{-1}\approx 1.2$
at inception (
$St_{L}^{-1}\approx 1.2$
at inception (
![]() $L/\unicode[STIX]{x1D6FF}_{o}=6.5$
,
$L/\unicode[STIX]{x1D6FF}_{o}=6.5$
,
![]() $M_{b}=1.84$
), compared to
$M_{b}=1.84$
), compared to
![]() $St_{L}^{-1}\approx 0.15$
here. As shown in figure 23(b), the latter case finds enhanced overlap in terms of
$St_{L}^{-1}\approx 0.15$
here. As shown in figure 23(b), the latter case finds enhanced overlap in terms of
![]() $St_{\unicode[STIX]{x1D6FF}}$
(
$St_{\unicode[STIX]{x1D6FF}}$
(
![]() $=f\unicode[STIX]{x1D6FF}_{o}/U_{b}$
, with reference to velocity behind the separation shock) and up to
$=f\unicode[STIX]{x1D6FF}_{o}/U_{b}$
, with reference to velocity behind the separation shock) and up to
![]() $X_{ej}^{\ast }\approx 0.5$
, where the shear layer leaves the incident shock interaction (cf.
$X_{ej}^{\ast }\approx 0.5$
, where the shear layer leaves the incident shock interaction (cf.
![]() $X_{ej}^{\ast }\approx 1$
in the FFS). As earlier noted (§ 3.2), the inception frequency appears more immediately scaled with the incoming flow so that for
$X_{ej}^{\ast }\approx 1$
in the FFS). As earlier noted (§ 3.2), the inception frequency appears more immediately scaled with the incoming flow so that for
![]() $f_{i}$
we explicitly refer to
$f_{i}$
we explicitly refer to
![]() $St_{i,\unicode[STIX]{x1D6FF}}=St_{\unicode[STIX]{x1D6FF}}$
(
$St_{i,\unicode[STIX]{x1D6FF}}=St_{\unicode[STIX]{x1D6FF}}$
(
![]() $U_{b}/U_{e}$
). While the higher
$U_{b}/U_{e}$
). While the higher
![]() $St_{i,\unicode[STIX]{x1D6FF}}\approx 1$
upon inception in Thomas et al. is in part associated with the low (subsonic) convection Mach number of
$St_{i,\unicode[STIX]{x1D6FF}}\approx 1$
upon inception in Thomas et al. is in part associated with the low (subsonic) convection Mach number of
![]() $M_{c}\approx 0.48$
, compared to
$M_{c}\approx 0.48$
, compared to
![]() $M_{c}=0.80$
–1.55 for the other cases (where
$M_{c}=0.80$
–1.55 for the other cases (where
![]() $St_{i,\unicode[STIX]{x1D6FF}}\approx 0.21$
), the inception process is expected to be influenced by further variables in a lesser extent (local temperature, viscosity, incoming turbulence, etc.).
$St_{i,\unicode[STIX]{x1D6FF}}\approx 0.21$
), the inception process is expected to be influenced by further variables in a lesser extent (local temperature, viscosity, incoming turbulence, etc.).

Figure 24. Streamwise evolution of shear layer instability along upstream separation for step heights in the range
![]() $1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
(showing alternate cases) at
$1.0\leqslant h/\unicode[STIX]{x1D6FF}_{o}\leqslant 5.9$
(showing alternate cases) at
![]() $M_{e}=3.9$
, as: (a)
$M_{e}=3.9$
, as: (a)
![]() $St_{L}^{-1}$
versus
$St_{L}^{-1}$
versus
![]() $X^{\ast }$
and (b)
$X^{\ast }$
and (b)
![]() $St_{\unicode[STIX]{x1D6FF}}^{-1}$
versus
$St_{\unicode[STIX]{x1D6FF}}^{-1}$
versus
![]() $X^{\ast }$
.
$X^{\ast }$
.
A similar scaling assessment is presented for the multi-scale Mach 3.9 interactions in figure 24(a), where the trend is seen to vary accordingly as the separation scale is changed. Following the relation in (5.1), we later refer to the
![]() $St_{L}/X^{\ast -1}$
ratio to evaluate the link with interaction low-frequency unsteadiness (§ 5.3). In
$St_{L}/X^{\ast -1}$
ratio to evaluate the link with interaction low-frequency unsteadiness (§ 5.3). In
![]() $St_{\unicode[STIX]{x1D6FF}}$
form (figure 24
b), the frequencies near separation are captured at the earlier noted common inception levels to then diverge given the scaling with interaction length, accounted within
$St_{\unicode[STIX]{x1D6FF}}$
form (figure 24
b), the frequencies near separation are captured at the earlier noted common inception levels to then diverge given the scaling with interaction length, accounted within
![]() $X^{\ast }$
(note again the
$X^{\ast }$
(note again the
![]() $St_{L}$
and
$St_{L}$
and
![]() $St_{\unicode[STIX]{x1D6FF}}$
scalings in the paper are all with reference to
$St_{\unicode[STIX]{x1D6FF}}$
scalings in the paper are all with reference to
![]() $U_{b}$
, except for the inception instability
$U_{b}$
, except for the inception instability
![]() $St_{i,\unicode[STIX]{x1D6FF}}$
which appears more directly driven by the upstream flow). As per figure 24(b), the
$St_{i,\unicode[STIX]{x1D6FF}}$
which appears more directly driven by the upstream flow). As per figure 24(b), the
![]() $St_{\unicode[STIX]{x1D6FF}}/X^{\ast -1}$
ratio is effectively equivalent to
$St_{\unicode[STIX]{x1D6FF}}/X^{\ast -1}$
ratio is effectively equivalent to
![]() $St_{L}/X^{\ast -1}(L/\unicode[STIX]{x1D6FF}_{o})^{-1}$
and is found to be better suited for extraction of specific values within the interaction length (e.g. at
$St_{L}/X^{\ast -1}(L/\unicode[STIX]{x1D6FF}_{o})^{-1}$
and is found to be better suited for extraction of specific values within the interaction length (e.g. at
![]() $X_{ej}^{\ast }$
), with a scaling at inception consistent with the observations above. Here, shorter interactions are found to attain greater slopes and then go down to
$X_{ej}^{\ast }$
), with a scaling at inception consistent with the observations above. Here, shorter interactions are found to attain greater slopes and then go down to
![]() $St_{L}/X^{\ast -1}\approx 1.5$
–1.8 (
$St_{L}/X^{\ast -1}\approx 1.5$
–1.8 (
![]() $\pm 5\,\%$
) for the large-scale Mach 3.0–3.9 cases, slightly above the
$\pm 5\,\%$
) for the large-scale Mach 3.0–3.9 cases, slightly above the
![]() $St_{L}/X^{\ast -1}\approx 1.2$
in Thomas et al. (
$St_{L}/X^{\ast -1}\approx 1.2$
in Thomas et al. (
![]() $L/\unicode[STIX]{x1D6FF}_{o}=2.1$
) and considerably higher than
$L/\unicode[STIX]{x1D6FF}_{o}=2.1$
) and considerably higher than
![]() $St_{L}/X^{\ast -1}=0.34$
in Dupont et al. (
$St_{L}/X^{\ast -1}=0.34$
in Dupont et al. (
![]() $L/\unicode[STIX]{x1D6FF}_{o}=6.5$
), as well as those in the incompressible flow studies by Cherry et al. (
$L/\unicode[STIX]{x1D6FF}_{o}=6.5$
), as well as those in the incompressible flow studies by Cherry et al. (
![]() $St_{L}/X^{\ast -1}\approx 0.5$
).
$St_{L}/X^{\ast -1}\approx 0.5$
).
5.3 Entrainment–recharge mechanism
The shear layer’s role in the low-frequency mechanism associated with the bubble’s decay–growth dynamics is eventually assessed in figure 25. As such, we hereby refer to the concept of incipient separation as that starting to exhibit mean reverse flow, i.e. whereby a recirculation is incipiently formed (e.g. see Dussauge & Piponniau Reference Dussauge and Piponniau2008, Souverein et al.
Reference Souverein, Dupont, Debiève, Dussauge, Van Oudheusden and Scarano2010). The following analysis thus goes on to evaluate the intuitive scaling of the pulsation time scale as
![]() $T_{o}=M_{B,rev}/{\dot{m}}_{ej}$
, where
$T_{o}=M_{B,rev}/{\dot{m}}_{ej}$
, where
![]() $M_{B,rev}$
is the mean reverse flow mass – that is, with bubble recharge essentially triggered as incipient separation conditions are approached.
$M_{B,rev}$
is the mean reverse flow mass – that is, with bubble recharge essentially triggered as incipient separation conditions are approached.
The
![]() $St_{L}/X^{\ast -1}$
slope is first compared to the interaction low-frequency unsteadiness in the form
$St_{L}/X^{\ast -1}$
slope is first compared to the interaction low-frequency unsteadiness in the form
![]() $St_{o,\unicode[STIX]{x1D6FF}}$
, to account for variations among the different flow conditions (figure 25
b). In those cases sufficiently above the incipience threshold and involving well-developed separation (
$St_{o,\unicode[STIX]{x1D6FF}}$
, to account for variations among the different flow conditions (figure 25
b). In those cases sufficiently above the incipience threshold and involving well-developed separation (
![]() $h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
) both quantities are found to decrease accordingly with interaction scale, thus sustaining a clear link between the two. Effectively,
$h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1.0$
) both quantities are found to decrease accordingly with interaction scale, thus sustaining a clear link between the two. Effectively,
![]() $St_{o,\unicode[STIX]{x1D6FF}}$
complies with the expected increase in pulsation time scales for larger interaction scales whilst the
$St_{o,\unicode[STIX]{x1D6FF}}$
complies with the expected increase in pulsation time scales for larger interaction scales whilst the
![]() $St_{L}/X^{\ast -1}$
ratio (from figures 23
a and 24
a) is in great part reduced through what appears to be an artificial scaling at inception – yet indirectly finding close similarity between the trends. Alternately,
$St_{L}/X^{\ast -1}$
ratio (from figures 23
a and 24
a) is in great part reduced through what appears to be an artificial scaling at inception – yet indirectly finding close similarity between the trends. Alternately,
![]() $St_{o,\unicode[STIX]{x1D6FF}}$
may be expressed to include separation length (from figure 8
a) to yield
$St_{o,\unicode[STIX]{x1D6FF}}$
may be expressed to include separation length (from figure 8
a) to yield
![]() $St_{o,\unicode[STIX]{x1D6FF}}^{-1}\approx 14L/\unicode[STIX]{x1D6FF}_{o}$
across the Mach 3.9 range – i.e. effectively
$St_{o,\unicode[STIX]{x1D6FF}}^{-1}\approx 14L/\unicode[STIX]{x1D6FF}_{o}$
across the Mach 3.9 range – i.e. effectively
![]() $St_{o,L}\approx 0.07$
. As evidenced in figure 25(c),
$St_{o,L}\approx 0.07$
. As evidenced in figure 25(c),
![]() $St_{o,L}$
remains at this level for all the Mach 3.9 cases involving well-developed separation, with similar values at Mach 3.0; the Mach 2.0 case instead differs slightly given the inherent differences at this lower Mach number. The evaluation against the ejection frequencies, accordingly shown here in terms of a Strouhal number
$St_{o,L}$
remains at this level for all the Mach 3.9 cases involving well-developed separation, with similar values at Mach 3.0; the Mach 2.0 case instead differs slightly given the inherent differences at this lower Mach number. The evaluation against the ejection frequencies, accordingly shown here in terms of a Strouhal number
![]() $St_{ej,L}$
(
$St_{ej,L}$
(
![]() $=f_{ej}L/U_{b}$
), finds both frequencies to vary proportionally as
$=f_{ej}L/U_{b}$
), finds both frequencies to vary proportionally as
![]() $St_{o,L}\approx 0.04St_{ej,L}$
, thus confirming a relation between the breathing and ejection rates, i.e. practically at
$St_{o,L}\approx 0.04St_{ej,L}$
, thus confirming a relation between the breathing and ejection rates, i.e. practically at
![]() $f_{o}\approx 0.04f_{ej}$
across the Mach 3.0–3.9 cases (
$f_{o}\approx 0.04f_{ej}$
across the Mach 3.0–3.9 cases (
![]() $M_{c}=1.25$
–1.55); while in the Mach 2.0 interaction (
$M_{c}=1.25$
–1.55); while in the Mach 2.0 interaction (
![]() $M_{c}=0.8$
) this is found to be slightly lower,
$M_{c}=0.8$
) this is found to be slightly lower,
![]() $f_{o}\approx 0.03f_{ej}$
. Despite the noted scaling with
$f_{o}\approx 0.03f_{ej}$
. Despite the noted scaling with
![]() $L$
, it is worth remarking that the mass in the bubble in fact varies effectively as
$L$
, it is worth remarking that the mass in the bubble in fact varies effectively as
![]() $M_{B}$
$M_{B}$
![]() $\propto$
$\propto$
![]() $L^{2}$
(figure 22
a), rendering the bubble recharge mechanism not immediately obvious – in part given the complex nature of the entrainment process, as discussed next.
$L^{2}$
(figure 22
a), rendering the bubble recharge mechanism not immediately obvious – in part given the complex nature of the entrainment process, as discussed next.

Figure 25. STBLI low-frequency unsteadiness: (a) schematic highlighting key flow features, (b) variation in shear layer evolution rate in the form
![]() $St_{L}/X^{\ast -1}$
(grey symbols, left axis) and in low-frequency unsteadiness as
$St_{L}/X^{\ast -1}$
(grey symbols, left axis) and in low-frequency unsteadiness as
![]() $St_{o,\unicode[STIX]{x1D6FF}}$
(white symbols, right axis) for complete range of steps considered in the study and (c) variation in low-frequency unsteadiness as
$St_{o,\unicode[STIX]{x1D6FF}}$
(white symbols, right axis) for complete range of steps considered in the study and (c) variation in low-frequency unsteadiness as
![]() $St_{o,L}$
(white symbols, right axis) to evaluate scaling with separation length, and compared with the respective Strouhal number upon ejection
$St_{o,L}$
(white symbols, right axis) to evaluate scaling with separation length, and compared with the respective Strouhal number upon ejection
![]() $St_{ej,L}$
(grey symbols, left axis). Horizontal and vertical dashed lines in panel (c) indicate
$St_{ej,L}$
(grey symbols, left axis). Horizontal and vertical dashed lines in panel (c) indicate
![]() $f_{o}\approx 0.04f_{ej}$
level and
$f_{o}\approx 0.04f_{ej}$
level and
![]() $h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1$
threshold. Symbol legend in
$h/\unicode[STIX]{x1D6FF}_{o}\geqslant 1$
threshold. Symbol legend in
![]() $St_{i,\unicode[STIX]{x1D6FF}}$
versus
$St_{i,\unicode[STIX]{x1D6FF}}$
versus
![]() $M_{c}$
plot as per figures 23(b) and 24(b) (including present dataset and reference studies marked as b in table 2).
$M_{c}$
plot as per figures 23(b) and 24(b) (including present dataset and reference studies marked as b in table 2).
For turbulent mixing layers (e.g. see the review by Dimotakis Reference Dimotakis2005), the spreading rate and entrainment ratio are widely reported to scale with the geometrical properties of large-scale shear layer structures, and here they practically appear to dominate the process of mass entrainment along the recirculation. This is broadly sustained by a number of studies to have documented the main role of engulfment at the scale of large eddies, generally finding negligible influence of both smaller-scale nibbling and locally induced velocities (e.g. Bisset, Hunt & Rogers Reference Bisset, Hunt and Rogers2002, Philip & Marusic Reference Philip and Marusic2012). It has earlier been established that, for a given convection Mach number
![]() $M_{c}$
, the shear layer’s spreading rate remains practically constant and its thickness grows linearly in the streamwise direction (
$M_{c}$
, the shear layer’s spreading rate remains practically constant and its thickness grows linearly in the streamwise direction (
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D6FF}^{\prime }X$
by definition), whereby eddies convect as intermittent discrete structures – with significant spanwise extent, presumably in the form of rollers covering a substantial portion of the perimeter (of order
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D6FF}^{\prime }X$
by definition), whereby eddies convect as intermittent discrete structures – with significant spanwise extent, presumably in the form of rollers covering a substantial portion of the perimeter (of order
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D711}\approx (10^{1}{-}10^{2})\unicode[STIX]{x1D6FF}_{o}$
, as per the azimuthal measurements in our earlier studies). Since eddy length intrinsically scales with the shear layer’s spreading rate and hence its local thickness
$\unicode[STIX]{x0394}\unicode[STIX]{x1D711}\approx (10^{1}{-}10^{2})\unicode[STIX]{x1D6FF}_{o}$
, as per the azimuthal measurements in our earlier studies). Since eddy length intrinsically scales with the shear layer’s spreading rate and hence its local thickness
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D700}}\propto \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
(defining
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D700}}\propto \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
(defining
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D700}}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
as the aspect ratio of eddy structures), eddy area – or rather their volume per unit span – is thus bound to exhibit a continued growth over the streamwise direction. While eddies are inherently irregular and three-dimensional (often with complex jagged geometry, e.g. as in Clemens & Mungal Reference Clemens and Mungal1995), they may be statistically modelled as large coherent structures with a given length-to-thickness ratio
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D700}}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
as the aspect ratio of eddy structures), eddy area – or rather their volume per unit span – is thus bound to exhibit a continued growth over the streamwise direction. While eddies are inherently irregular and three-dimensional (often with complex jagged geometry, e.g. as in Clemens & Mungal Reference Clemens and Mungal1995), they may be statistically modelled as large coherent structures with a given length-to-thickness ratio
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}$
, from a simplistic approach (next approximated to comply with an elliptical geometry). As discussed in § 4.3, eddy growth is in turn naturally sustained through the progressive entrainment from the surrounding flow, partly from the separation, as structures evolve along the interaction. The basis for these premises fundamentally stems from the incompressible mixing layer studies by Brown & Roshko (Reference Brown and Roshko1974) which, despite the expected inaccuracies given the highly simplified nature of the scalings, are argued to rely on physically correct interpretations, adequate for the assessment of the unfolding tendencies.
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}$
, from a simplistic approach (next approximated to comply with an elliptical geometry). As discussed in § 4.3, eddy growth is in turn naturally sustained through the progressive entrainment from the surrounding flow, partly from the separation, as structures evolve along the interaction. The basis for these premises fundamentally stems from the incompressible mixing layer studies by Brown & Roshko (Reference Brown and Roshko1974) which, despite the expected inaccuracies given the highly simplified nature of the scalings, are argued to rely on physically correct interpretations, adequate for the assessment of the unfolding tendencies.
Describing the process to be physically driven by flow entrainment at the scale of large eddy structures – and following a similar rationale as in Brown & Roshko (Reference Brown and Roshko1974) (in their original form described as circular eddies at low speeds) – we may hereby express the rate of mass ejection as:
where
![]() $\dot{Q}_{ej}$
is the volume flow rate (per unit span) depleted from the separation by an elliptical eddy structure with aspect ratio
$\dot{Q}_{ej}$
is the volume flow rate (per unit span) depleted from the separation by an elliptical eddy structure with aspect ratio
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}$
and at a rate
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}$
and at a rate
![]() $f_{ej}$
(at
$f_{ej}$
(at
![]() ${\sim}X_{ej}^{\ast }$
);
${\sim}X_{ej}^{\ast }$
);
![]() $\unicode[STIX]{x1D709}_{B}$
is the percentage of mass acquired by eddies from the inner separation, i.e. with (1–
$\unicode[STIX]{x1D709}_{B}$
is the percentage of mass acquired by eddies from the inner separation, i.e. with (1–
![]() $\unicode[STIX]{x1D709}_{B}$
) being the contribution from the outer side.
$\unicode[STIX]{x1D709}_{B}$
) being the contribution from the outer side.
The time scale of bubble breathing then becomes:
where the mass of the reverse flow in the bubble is accounted for through a ratio
![]() $\unicode[STIX]{x1D705}_{R}=M_{B,rev}/M_{B}$
, effectively
$\unicode[STIX]{x1D705}_{R}=M_{B,rev}/M_{B}$
, effectively
![]() $\unicode[STIX]{x1D705}_{R}=1/2$
through mass conservation assumptions for a quasi-steady recirculation (here with stagnation line extrapolated to approximately half the step height). Shear layer spreading rate is primarily a function of Mach number and is estimated as
$\unicode[STIX]{x1D705}_{R}=1/2$
through mass conservation assumptions for a quasi-steady recirculation (here with stagnation line extrapolated to approximately half the step height). Shear layer spreading rate is primarily a function of Mach number and is estimated as
![]() $\unicode[STIX]{x1D6FF}^{\prime }=0.05$
across the Mach 3.9 range, and hence
$\unicode[STIX]{x1D6FF}^{\prime }=0.05$
across the Mach 3.9 range, and hence
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},ej}\approx 0.05L$
(Smits & Dussauge Reference Smits and Dussauge2006a
); this is also similar for the
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},ej}\approx 0.05L$
(Smits & Dussauge Reference Smits and Dussauge2006a
); this is also similar for the
![]() $M_{e}=3.0$
cases and approximately twice as high at
$M_{e}=3.0$
cases and approximately twice as high at
![]() $M_{e}=2.0$
(
$M_{e}=2.0$
(
![]() $\unicode[STIX]{x1D6FF}^{\prime }=0.10$
). While entrainment is bound to be locally asymmetric and potentially vary over the shear layer’s path along the bubble, we can cautiously estimate
$\unicode[STIX]{x1D6FF}^{\prime }=0.10$
). While entrainment is bound to be locally asymmetric and potentially vary over the shear layer’s path along the bubble, we can cautiously estimate
![]() $\unicode[STIX]{x1D709}_{B}\approx 50\,\%$
– i.e. with an approximately even contribution to eddy growth between the inner separation and outer sides.
$\unicode[STIX]{x1D709}_{B}\approx 50\,\%$
– i.e. with an approximately even contribution to eddy growth between the inner separation and outer sides.
Interaction low-frequency unsteadiness would therefore comply with:
this appearing broadly consistent with the final correlations in figure 25(c), which have earlier been noted to remain within
![]() $f_{o}\approx 0.04f_{ej}$
across the Mach 3.0–3.9 cases (tentatively conforming to an aspect ratio of eddy structures of order
$f_{o}\approx 0.04f_{ej}$
across the Mach 3.0–3.9 cases (tentatively conforming to an aspect ratio of eddy structures of order
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}\approx 2$
, as based on the given estimates), with a departure from the above relation being instead found for the Mach 2.0 case (
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}\approx 2$
, as based on the given estimates), with a departure from the above relation being instead found for the Mach 2.0 case (
![]() $f_{o}\approx 0.03f_{ej}$
). From an ad hoc approach, this latter equivalence would be effectively met for a circular eddy structure
$f_{o}\approx 0.03f_{ej}$
). From an ad hoc approach, this latter equivalence would be effectively met for a circular eddy structure
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=1$
with reduced relative entrainment
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=1$
with reduced relative entrainment
![]() $\unicode[STIX]{x1D709}_{B}\approx 25\,\%$
(far from a rigorous estimate, but assuming the other constants in equation (5.4) to be less prone to uncertainty). Essentially, while the large eddies could be potentially modelled to adopt a simplified elliptical shape at high convective speeds, where coherent turbulent structures are typically elongated (with relatively reduced lateral spreading rates, e.g. Fiala, Hillier and Estruch-Samper Reference Fiala, Hillier and Estruch-Samper2014), their geometry could be therefore deemed to become accordingly less slender, tending to circular (
$\unicode[STIX]{x1D709}_{B}\approx 25\,\%$
(far from a rigorous estimate, but assuming the other constants in equation (5.4) to be less prone to uncertainty). Essentially, while the large eddies could be potentially modelled to adopt a simplified elliptical shape at high convective speeds, where coherent turbulent structures are typically elongated (with relatively reduced lateral spreading rates, e.g. Fiala, Hillier and Estruch-Samper Reference Fiala, Hillier and Estruch-Samper2014), their geometry could be therefore deemed to become accordingly less slender, tending to circular (
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}\rightarrow 1$
) at lower
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}\rightarrow 1$
) at lower
![]() $M_{c}$
.
$M_{c}$
.
The depletion process is thus sustained to be in essence driven by the state of eddies upon their departure from the separation, rendering the mechanism particularly sensitive to the shear layer spreading rate
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
, as well as to the relative ejection location
$\unicode[STIX]{x1D6FF}^{\prime }$
, as well as to the relative ejection location
![]() $X_{ej}^{\ast }$
specific to the configuration – whereby
$X_{ej}^{\ast }$
specific to the configuration – whereby
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},ej}=\unicode[STIX]{x1D6FF}^{\prime }(LX_{ej}^{\ast })$
. As evidenced in the supplementary high-speed schlieren movie (clip available online), eddies appear practically ejected at this location with negligible re-incidence into the bubble (only apparent in occasional events, at much lower frequencies). Therefore, while the pressure spectra near the step strictly document the perturbations associated with the local eddy ‘passage rate’, it thus seems safe to practically interpret them as a measure of ejection frequency
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},ej}=\unicode[STIX]{x1D6FF}^{\prime }(LX_{ej}^{\ast })$
. As evidenced in the supplementary high-speed schlieren movie (clip available online), eddies appear practically ejected at this location with negligible re-incidence into the bubble (only apparent in occasional events, at much lower frequencies). Therefore, while the pressure spectra near the step strictly document the perturbations associated with the local eddy ‘passage rate’, it thus seems safe to practically interpret them as a measure of ejection frequency
![]() $f_{ej}$
. The simplistic scaling in equation (5.2), viewed from a statistical perspective, may further be seen to attribute a progressive growth in the separated mass carried by eddies as they evolve along the bubble
$f_{ej}$
. The simplistic scaling in equation (5.2), viewed from a statistical perspective, may further be seen to attribute a progressive growth in the separated mass carried by eddies as they evolve along the bubble
![]() $m_{\unicode[STIX]{x1D700}}$
(
$m_{\unicode[STIX]{x1D700}}$
(
![]() $=0.25\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D709}_{B}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}^{2}\unicode[STIX]{x1D70C}_{B}$
), with
$=0.25\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D709}_{B}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}^{2}\unicode[STIX]{x1D70C}_{B}$
), with
![]() $f_{ej}$
in turn determining the shedding rate upon ejection. This may be in part expected since eddies can be safely assumed to be isolated (not coalesced), with local convection time scales several times shorter than the respective lapse times between their passage,
$f_{ej}$
in turn determining the shedding rate upon ejection. This may be in part expected since eddies can be safely assumed to be isolated (not coalesced), with local convection time scales several times shorter than the respective lapse times between their passage,
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D700}}/U_{c}<\unicode[STIX]{x1D70F}_{x}$
(where
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D700}}/U_{c}<\unicode[STIX]{x1D70F}_{x}$
(where
![]() $\unicode[STIX]{x1D70F}_{x}\approx f_{ch}^{-1}$
). From a Eulerian perspective, the entrainment process may therefore be seen to extend from close downstream of separation all the way down to ejection, and a distinction is hereby drawn between the concepts of: (i) local entrainment rate
$\unicode[STIX]{x1D70F}_{x}\approx f_{ch}^{-1}$
). From a Eulerian perspective, the entrainment process may therefore be seen to extend from close downstream of separation all the way down to ejection, and a distinction is hereby drawn between the concepts of: (i) local entrainment rate
![]() ${\dot{m}}_{x}$
(
${\dot{m}}_{x}$
(
![]() $=\text{d}m_{\unicode[STIX]{x1D700}}/\,\text{d}t$
), as the rate of separated mass ingested at a given axial location, and (ii) the separated mass carried/accumulated within eddies
$=\text{d}m_{\unicode[STIX]{x1D700}}/\,\text{d}t$
), as the rate of separated mass ingested at a given axial location, and (ii) the separated mass carried/accumulated within eddies
![]() $m_{\unicode[STIX]{x1D700}}$
, resulting from their integral effect as they evolve along the bubble (
$m_{\unicode[STIX]{x1D700}}$
, resulting from their integral effect as they evolve along the bubble (
![]() $=\int _{0}^{t_{c}}{\dot{m}}_{x}\,\text{d}t$
, where
$=\int _{0}^{t_{c}}{\dot{m}}_{x}\,\text{d}t$
, where
![]() $t_{c}\approx X/U_{c}$
is the convection time since inception). To illustrate the latter, estimates on the
$t_{c}\approx X/U_{c}$
is the convection time since inception). To illustrate the latter, estimates on the
![]() $m_{\unicode[STIX]{x1D700}}$
evolution for different cases are given in figure 26, whereby the rate of mass depletion is noted to be a function of the separated mass cumulatively entrained up to their ejection and the local shedding rate,
$m_{\unicode[STIX]{x1D700}}$
evolution for different cases are given in figure 26, whereby the rate of mass depletion is noted to be a function of the separated mass cumulatively entrained up to their ejection and the local shedding rate,
![]() ${\dot{m}}_{ej}=m_{\unicode[STIX]{x1D700}}f_{ej}$
.
${\dot{m}}_{ej}=m_{\unicode[STIX]{x1D700}}f_{ej}$
.
As per the tendencies in figures 23(b) and 24(b), the rate upon ejection may be seen to be intrinsically dictated by the inception instability
![]() $St_{i,\unicode[STIX]{x1D6FF}}$
and its subsequent evolution as:
$St_{i,\unicode[STIX]{x1D6FF}}$
and its subsequent evolution as:
where the present inception levels of
![]() $St_{i,\unicode[STIX]{x1D6FF}}\approx 0.21$
are relatively close – maybe coincidentally – to those in Dupont et al.’s Mach 2.3 incident shock interactions (
$St_{i,\unicode[STIX]{x1D6FF}}\approx 0.21$
are relatively close – maybe coincidentally – to those in Dupont et al.’s Mach 2.3 incident shock interactions (
![]() $M_{c}\approx 0.92$
). Through analogy with the typical Strouhal numbers reported for the shedding past an obstacle, at
$M_{c}\approx 0.92$
). Through analogy with the typical Strouhal numbers reported for the shedding past an obstacle, at
![]() $Re_{\unicode[STIX]{x1D6FF}}=10^{3}$
–
$Re_{\unicode[STIX]{x1D6FF}}=10^{3}$
–
![]() $10^{5}$
(for a length scale
$10^{5}$
(for a length scale
![]() ${\sim}\unicode[STIX]{x1D6FF}_{o}$
), the origin of the instability could thus be expected to lie in a similar mechanism of locally induced vorticity within the near-wall region, close behind separation – this potentially differing in interactions with relatively small-scale separation or nearing the subsonic shear layer regime (bearing in mind this remains largely unestablished given the limited nature of the dataset). As such, the inception Strouhal numbers
${\sim}\unicode[STIX]{x1D6FF}_{o}$
), the origin of the instability could thus be expected to lie in a similar mechanism of locally induced vorticity within the near-wall region, close behind separation – this potentially differing in interactions with relatively small-scale separation or nearing the subsonic shear layer regime (bearing in mind this remains largely unestablished given the limited nature of the dataset). As such, the inception Strouhal numbers
![]() $St_{i,\unicode[STIX]{x1D6FF}}$
in the available dataset are included in figure 25(a), indicating a tentative tendency towards
$St_{i,\unicode[STIX]{x1D6FF}}$
in the available dataset are included in figure 25(a), indicating a tentative tendency towards
![]() $St_{i,\unicode[STIX]{x1D6FF}}\rightarrow 1$
at low subsonic convection Mach numbers
$St_{i,\unicode[STIX]{x1D6FF}}\rightarrow 1$
at low subsonic convection Mach numbers
![]() $M_{c}$
, where local vorticity near separation would be in principle reduced.
$M_{c}$
, where local vorticity near separation would be in principle reduced.

Figure 26. Estimated evolution of separated mass carried by large shear layer eddies
![]() $m_{\unicode[STIX]{x1D700}}$
(left axis), shown also with reference to ejected mass at
$m_{\unicode[STIX]{x1D700}}$
(left axis), shown also with reference to ejected mass at
![]() $X_{ej}^{\ast }\approx 1$
for the highly separated Mach 3.9 case (
$X_{ej}^{\ast }\approx 1$
for the highly separated Mach 3.9 case (
![]() $m_{\unicode[STIX]{x1D700},ref}\approx 8.5\times 10^{-6}~\text{kg}~\text{m}^{-1}$
, right axis) and whereby the rate of mass ejection is
$m_{\unicode[STIX]{x1D700},ref}\approx 8.5\times 10^{-6}~\text{kg}~\text{m}^{-1}$
, right axis) and whereby the rate of mass ejection is
![]() ${\dot{m}}_{ej}=m_{\unicode[STIX]{x1D700}}f_{ej}$
(
${\dot{m}}_{ej}=m_{\unicode[STIX]{x1D700}}f_{ej}$
(
![]() ${\dot{m}}_{ej,ref}\approx 0.075~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
). Trends assume constant shear layer growth
${\dot{m}}_{ej,ref}\approx 0.075~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
). Trends assume constant shear layer growth
![]() $\unicode[STIX]{x1D6FF}^{\prime }=0.05$
for Mach 3.0–3.9 cases (
$\unicode[STIX]{x1D6FF}^{\prime }=0.05$
for Mach 3.0–3.9 cases (
![]() $M_{c}\geqslant 1.25$
) and
$M_{c}\geqslant 1.25$
) and
![]() $\unicode[STIX]{x1D6FF}^{\prime }=0.10$
at Mach 2.0 (based on (5.2) and taking
$\unicode[STIX]{x1D6FF}^{\prime }=0.10$
at Mach 2.0 (based on (5.2) and taking
![]() $\unicode[STIX]{x1D709}_{B}\approx 0.5$
and
$\unicode[STIX]{x1D709}_{B}\approx 0.5$
and
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=2$
for cases with
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=2$
for cases with
![]() $M_{c}\gg 0.8$
; taking
$M_{c}\gg 0.8$
; taking
![]() $\unicode[STIX]{x1D709}_{B}\approx 0.25$
and
$\unicode[STIX]{x1D709}_{B}\approx 0.25$
and
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=1$
when
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}=1$
when
![]() $M_{c}\leqslant 0.8$
). Figure includes estimates for Thomas et al.’s Mach 1.5 CC interaction where
$M_{c}\leqslant 0.8$
). Figure includes estimates for Thomas et al.’s Mach 1.5 CC interaction where
![]() ${\dot{m}}_{ej}=0.021\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
(
${\dot{m}}_{ej}=0.021\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
(
![]() $\unicode[STIX]{x1D70C}_{B}=0.63~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D70C}_{B}=0.63~\text{kg}~\text{m}^{-3}$
,
![]() $\unicode[STIX]{x1D6FF}^{\prime }=0.13$
, with
$\unicode[STIX]{x1D6FF}^{\prime }=0.13$
, with
![]() $f_{ej}=11~\text{kHz}$
at
$f_{ej}=11~\text{kHz}$
at
![]() $X_{ej}^{\ast }\approx 1$
); Dupont et al.’s Mach 2.3 IS interaction is shown at a factor
$X_{ej}^{\ast }\approx 1$
); Dupont et al.’s Mach 2.3 IS interaction is shown at a factor
![]() $\times 10$
higher for comparison, where
$\times 10$
higher for comparison, where
![]() ${\dot{m}}_{ej}=0.0025\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
(
${\dot{m}}_{ej}=0.0025\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
(
![]() $\unicode[STIX]{x1D70C}_{B}=0.081~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D70C}_{B}=0.081~\text{kg}~\text{m}^{-3}$
,
![]() $\unicode[STIX]{x1D6FF}^{\prime }=0.08$
, with
$\unicode[STIX]{x1D6FF}^{\prime }=0.08$
, with
![]() $f_{ej}=5~\text{kHz}$
at
$f_{ej}=5~\text{kHz}$
at
![]() $X_{ej}^{\ast }\approx 0.5$
). *Perturbations with streamwise directivity. Symbol legend as per figures 23–25.
$X_{ej}^{\ast }\approx 0.5$
). *Perturbations with streamwise directivity. Symbol legend as per figures 23–25.
5.4 Low-frequency unsteadiness prediction
On the whole, the prediction of STBLI low-frequency unsteadiness
![]() $f_{o}$
would thus implicitly rely on accurate estimates of shear layer growth and its entrainment dynamics, to account for
$f_{o}$
would thus implicitly rely on accurate estimates of shear layer growth and its entrainment dynamics, to account for
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
,
$\unicode[STIX]{x1D6FF}^{\prime }$
,
![]() $X_{ej}^{\ast }$
,
$X_{ej}^{\ast }$
,
![]() $f_{ej}$
(hence inception conditions), together with
$f_{ej}$
(hence inception conditions), together with
![]() $\unicode[STIX]{x1D709}_{B}$
and details on the asymmetric evolution of turbulent shear layer structures – in addition to those properties more immediately related to the mean separation (e.g.
$\unicode[STIX]{x1D709}_{B}$
and details on the asymmetric evolution of turbulent shear layer structures – in addition to those properties more immediately related to the mean separation (e.g.
![]() $L$
,
$L$
,
![]() $h$
,
$h$
,
![]() $\unicode[STIX]{x1D705}_{R}$
). With this in mind, a fundamental aim of the investigation has been to obtain accurate measurements of the main quantities involved, with the axisymmetric nature of the dataset further allowing us to discard the influence of added effects to some extent present in planar configurations. To this end, the study has striven to experimentally characterise interaction unsteadiness at relatively high spatial and frequency resolutions (reliably up to 50 kHz, over durations of order
$\unicode[STIX]{x1D705}_{R}$
). With this in mind, a fundamental aim of the investigation has been to obtain accurate measurements of the main quantities involved, with the axisymmetric nature of the dataset further allowing us to discard the influence of added effects to some extent present in planar configurations. To this end, the study has striven to experimentally characterise interaction unsteadiness at relatively high spatial and frequency resolutions (reliably up to 50 kHz, over durations of order
![]() $10^{3}$
–
$10^{3}$
–
![]() $10^{4}T_{o}$
) and through systematic variations in separated mass. Results render the large shear layer eddies as the immediate drivers of the low-frequency mechanism, with the total mass depleted over each cycle deemed to be induced by approximately
$10^{4}T_{o}$
) and through systematic variations in separated mass. Results render the large shear layer eddies as the immediate drivers of the low-frequency mechanism, with the total mass depleted over each cycle deemed to be induced by approximately
![]() $\unicode[STIX]{x1D716}_{ej}=25$
ejection events (eddies leaving the separation per pulsation,
$\unicode[STIX]{x1D716}_{ej}=25$
ejection events (eddies leaving the separation per pulsation,
![]() $\unicode[STIX]{x1D716}_{ej}\approx f_{ej}/f_{o}$
) across the present Mach 3.0–3.9 range. Determining precisely the mass entrained at the scale of large eddies remains particularly challenging – this being here simplistically modelled as per (5.2) for evaluation purposes (and arguably the most complex measure in the analysis).
$\unicode[STIX]{x1D716}_{ej}\approx f_{ej}/f_{o}$
) across the present Mach 3.0–3.9 range. Determining precisely the mass entrained at the scale of large eddies remains particularly challenging – this being here simplistically modelled as per (5.2) for evaluation purposes (and arguably the most complex measure in the analysis).
As further assessed in figure 26, these observations would be consistent with the estimates of
![]() ${\dot{m}}_{ej}=0.021\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
and
${\dot{m}}_{ej}=0.021\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
and
![]() $M_{B,rev}\approx 2.0\times 10^{-5}~\text{kg}~\text{m}^{-1}$
for the Mach 1.5 compression corner interaction from Thomas et al. (
$M_{B,rev}\approx 2.0\times 10^{-5}~\text{kg}~\text{m}^{-1}$
for the Mach 1.5 compression corner interaction from Thomas et al. (
![]() $f_{o}=1~\text{kHz}$
, see table 2); as well as with Dupont et al.’s incident shock interaction (
$f_{o}=1~\text{kHz}$
, see table 2); as well as with Dupont et al.’s incident shock interaction (
![]() $f_{o}=171$
Hz), whereby similar considerations would lead to estimates of
$f_{o}=171$
Hz), whereby similar considerations would lead to estimates of
![]() ${\dot{m}}_{ej}=0.0025\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
and
${\dot{m}}_{ej}=0.0025\pm 10\,\%~\text{kg}~\text{s}^{-1}~\text{m}^{-1}$
and
![]() $M_{B,rev}\approx 1.45\times 10^{-5}~\text{kg}~\text{m}^{-1}$
. Noting the order of magnitude differences in the measured
$M_{B,rev}\approx 1.45\times 10^{-5}~\text{kg}~\text{m}^{-1}$
. Noting the order of magnitude differences in the measured
![]() $f_{o}$
, and being specially cautious with the scalings of
$f_{o}$
, and being specially cautious with the scalings of
![]() ${\dot{m}}_{ej}$
given the highly simplified modelling of their entrainment dynamics (e.g. where
${\dot{m}}_{ej}$
given the highly simplified modelling of their entrainment dynamics (e.g. where
![]() $\unicode[STIX]{x1D709}_{B}$
,
$\unicode[STIX]{x1D709}_{B}$
,
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}$
, etc. are clearly prone to uncertainties), the time scale
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}$
, etc. are clearly prone to uncertainties), the time scale
![]() $T_{o}=M_{B,rev}/{\dot{m}}_{ej}$
thus appears broadly coherent with these estimates as well. On this account, the entrainment–recharge mechanism would in principle apply to other configurations regardless of the source of separation, and to some extent also complies with observations in past incompressible separation studies (e.g. Cherry, Hillier & Latour Reference Cherry, Hillier and Latour1984).
$T_{o}=M_{B,rev}/{\dot{m}}_{ej}$
thus appears broadly coherent with these estimates as well. On this account, the entrainment–recharge mechanism would in principle apply to other configurations regardless of the source of separation, and to some extent also complies with observations in past incompressible separation studies (e.g. Cherry, Hillier & Latour Reference Cherry, Hillier and Latour1984).
Within the noted uncertainties intrinsic to the entrainment–recharge dynamics, results have enabled us to experimentally identify and examine some the fundamental tendencies upon which the proposed views were built. From a broader perspective, it is suggested that high-fidelity predictions of STBLI unsteadiness could greatly benefit from the integration of extended empirical datasets – ideally including both canonical and flight test data – with accurate estimates of the shear layer’s entrainment (and subsequent ejection) process through advanced numerical simulation.
6 Conclusions
An experimental programme has been conducted to investigate the role of the separated shear layer across a range of axisymmetric STBLIs. Having established a dominant influence of shear layer perturbations in interactions with well-developed separation – whereby incoming turbulence takes up a secondary, less prominent role – the link between the shear layer and the low-frequency bubble pulsations has been explored. Results sustain a co-existence of both upstream and downstream influences, with the separated shear layer as the main driver of low-frequency unsteadiness: (i) the incoming boundary layer is suggested to bear an immediate influence on shear layer inception, with the initial shear layer instabilities proving independent of downstream effects – broadly in accordance with free-interaction theory; (ii) thereafter, eddies evolve along the recirculation region, entraining part of the separated flow along their way and depleting the bubble as they are intermittently ejected.
While the shear layer’s spreading rate is practically constant, the mass cumulatively entrained at the scale of large eddies – seen as discrete intermittent structures – increases progressively as they grow in the streamwise direction (deemed roughly proportional to their capacity, with a linear increase in thickness), with their ability to entrain the surrounding flow being enhanced as they evolve. As such, the amount of flow carried with them as they leave the separation is primarily determined by the local shedding rate and is as well intrinsically dependent on shear layer length and other related variables (mean flow organisation, spreading rate, entrainment dynamics, etc.). Having characterised some of the key aspects of the entrainment–recharge mechanism, the frequency of bubble breathing is confirmed to scale effectively as the ratio of ‘mass ejection rate’ to ‘reversed flow mass’,
![]() $f_{o}={\dot{m}}_{ej}/M_{B,rev}$
.
$f_{o}={\dot{m}}_{ej}/M_{B,rev}$
.
This would broadly apply to regions of high-speed turbulent boundary-layer separation, with both upstream and downstream influences playing important roles, as detailed in the hereby proposed view of the mechanism.
Acknowledgements
This research was supported by the Ministry of Education (MOE) Singapore through Academic Research Fund (AcRF) Tier 1 grant R-265-000-482-133. G.C. is a recipient of National University of Singapore (NUS) PhD Scholarship.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/jfm.2018.350.
































