Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T14:50:12.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Sensitivity of stratified turbulence to the buoyancy Reynolds number

Published online by Cambridge University Press:  14 May 2013

P. Bartello  and
S. M. Tobias
P. Bartello*
Affiliation:
Departments of Mathematics & Statistics and Atmospheric & Oceanic Sciences, McGill University, 805 rue Sherbrooke ouest, Montréal, Québec, H3A 0B9 Canada
S. M. Tobias
Affiliation:
Department of Mathematics, University of Leeds, Woodhouse Lane, Leeds, LS2 9JT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we present direct numerical simulations of stratified flow at resolutions of up to $204{8}^{2} \times 513$, to explore scalings for the dynamics of stably stratified turbulence. Recent work suggests that for strong enough stratification, the vertical integral scale of the turbulence adjusts to yield a vertical Froude number, 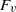${F}_{v} $, of order unity at high enough Reynolds number, whilst the horizontal Froude number, 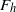${F}_{h} $, decreases as stratification is increased. Our numerical simulations are consistent with predictions by Lindborg (J. Fluid Mech., vol. 550, 2006, pp, 207–242), and with numerical simulations at lower resolution, in that the horizontal kinetic energy spectrum follows a Kolmogorov spectrum (after replacing the wavenumber with the horizontal wavenumber) and that the horizontal potential energy spectrum similarly follows the Corrsin–Obukhov spectrum for a passive scalar. Most importantly, we build upon these previous results by thoroughly exploring the dependence of the horizontal spectrum of horizontal kinetic energy on both the stratification and the relative size of the vertical dissipation terms, as quantified by the buoyancy Reynolds number. Our most important result is that variations in the power-law exponent scale entirely with the buoyancy Reynolds number and not with the stratification itself, lending considerable support to the Lindborg (2006) hypothesis that horizontal spectra are independent of stratification at large Reynolds numbers. We further demonstrate that even at the large numerical resolution of this study, the spectrum and hence the dynamics are affected by the buoyancy Reynolds number unless it is larger than 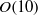$O(10)$, indicating that extreme care must be taken when assessing claims made from previous numerical simulations of stratified flow at low or moderate resolution and extrapolating the results to geophysical or astrophysical Reynolds numbers.

JFM classification

Geophysical and Geological Flows: Stratified flows Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 1 - 22
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babin, A., Mahalov, A. & Nicolaenko, B. 1997 On the asymptotic regimes and the strongly stratified limit of rotating Boussinesq equations. Theor. Comput. Fluid Dyn. 9, 223–251.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Cambon, C. F. & Scott, J. F. 1999 Linear and nonlinear models of anisotropic turbulence. Annu. Rev. Fluid Mech. 31, 1–53.CrossRefGoogle Scholar
Carnevale, G. F., Briscolini, M. & Orlandi, P. 2001 Buoyancy to inertial range transition in forced stratified turbulence. J. Fluid Mech. 427, 205–239.CrossRefGoogle Scholar
Cattaneo, F., Emonet, T. & Weiss, N. 2003 On the interaction between convection and magnetic fields. Astrophys. J. 588, 1183–1198.CrossRefGoogle Scholar
Dewan, E. M. & Good, R. E. 1986 Saturation and the ‘universal’ spectrum for vertical profiles of horizontal scalar winds in the atmosphere. J. Geophys. Res. 91, 2742–2748.CrossRefGoogle Scholar
Gough, D. O. & McIntyre, M. E. 1998 Inevitability of a magnetic field in the Sun’s radiative interior. Nature 394, 755–757.CrossRefGoogle Scholar
Herring, J. R. & Métais, O. 1989 Numerical experiments in forced stably-stratified turbulence. J. Fluid Mech. 202, 97–115.CrossRefGoogle Scholar
Kimura, Y. & Herring, J. R. 2012 Energy spectra of stably stratified turbulence. J. Fluid Mech. 698, 19–50.CrossRefGoogle Scholar
Klymak, J. M. & Moum, J. N. 2007 Oceanic isopycnal slope spectra. Part II: Turbulence. J. Phys. Oceanogr. 37, 1232–1245.CrossRefGoogle Scholar
Laval, J.-P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transitions with Reynolds number. Phys. Rev. E 68, 036308.CrossRefGoogle ScholarPubMed
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Phys. 40, 749–761.2.0.CO;2>CrossRefGoogle Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Lindborg, E. & Brethouwer, G. 2007 Stratified turbulence forced in rotational and divergent modes. J. Fluid Mech. 586, 83–108.CrossRefGoogle Scholar
McIntyre, M. E. 2003 Solar tachocline dynamics: eddy viscosity, anti-friction, or something in between? In Stellar Astrophysical Fluid Dynamics (ed. Thompson, M. J. & Christensen-Dalsgaard, J.), pp. 111–130. Provided by the SAO/NASA Astrophysics Data System. http://adsabs.harvard.edu/abs/2003safd.book..111M.CrossRefGoogle Scholar
Miesch, M. S. 2000 Large-scale dynamics of the convection zone and tachocline. Living Rev. Solar Phys. 2, 1.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.CrossRefGoogle Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.2.0.CO;2>CrossRefGoogle Scholar
Ozmidov, R. V. 1965 On the distribution of energy of motions of various scales in the ocean. Atmos. Ocean. Phys. 1, 257–279.Google Scholar
Read, P. L. 2011 Dynamics and circulation regimes of terrestrial planets. Planet. Space Sci. 59, 900–914.CrossRefGoogle Scholar
Riley, J. J. & deBruynKops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. J. Fluid Mech. 15, 2047–2059.Google Scholar
Riley, J. J., Metcalfe, R. W. & Weissman, M. A. 1981 Direct numerical simulations of homogeneous turbulence in density stratified fluids. In Nonlinear Properties of Internal Waves (ed. West, B. J.), AIP Conf. Proc., vol. 76. pp. 79–112.Google Scholar
Scott, R. K. & Polvani, L. M. 2008 Equatorial superrotation in shallow atmospheres. Geophys. Res. Lett. 352, L24202.Google Scholar
Smyth, W. D. & Moum, J. 2000 Anisotropy of turbulence in stably stratified mixing layers. Phys. Fluids 12, 1343–1362.CrossRefGoogle Scholar
Spiegel, E. A. & Zahn, J.-P. 1992 The solar tachocline. Astron. Astrophys. 265, 106–114.Google Scholar
Tobias, S. M. 2005 The solar tachocline: formation, stability and its role in the solar dynamo. In Fluid Dynamics and Dynamos in Astrophysics and Geophysics (ed. A. M. Soward, C. A. Jones, D. W. Hughes & N. O. Weiss), vol. 193. Provided by the SAO/NASA Astrophysics Data System. http://adsabs.harvard.edu/abs/2005fdda.conf..193T.CrossRefGoogle Scholar
Tobias, S. M., Cattaneo, F. & Brummell, N. H. 2008 Convective dynamos with penetration, rotation, and shear. Astrophys. J. 685, 596–605.CrossRefGoogle Scholar
Tobias, S. M., Diamond, P. H. & Hughes, D. W. 2007 $\beta $ -plane magnetohydrodynamic turbulence in the solar tachocline. Astrophys. Lett. Commun. 667, L113–L116.CrossRefGoogle Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Dynamcs Fundamentals and Large-scale Circulation. Cambridge University Press.Google Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2006 Stratified turbulence generated by internal gravity waves. J. Fluid Mech. 546, 313–339.CrossRefGoogle Scholar
Werne, J. & Fritts, D. C. 1999 Stratified shear turbulence: evolution and statistics. Geophys. Res. Lett. 26 26, 439–441.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar