Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T21:15:47.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similar rupture of thin films of power-law fluids on a substrate

Published online by Cambridge University Press:  04 August 2017

Vishrut Garg ,
Pritish M. Kamat ,
Christopher R. Anthony ,
Sumeet S. Thete  and
Osman A. Basaran Open the ORCID record for Osman A. Basaran [Opens in a new window]
Vishrut Garg
Affiliation:
School of Chemical Engineering, Purdue University, West Lafayette, IN 47907-1283, USA
Pritish M. Kamat
Affiliation:
School of Chemical Engineering, Purdue University, West Lafayette, IN 47907-1283, USA
Christopher R. Anthony
Affiliation:
School of Chemical Engineering, Purdue University, West Lafayette, IN 47907-1283, USA
Sumeet S. Thete
Affiliation:
School of Chemical Engineering, Purdue University, West Lafayette, IN 47907-1283, USA
Osman A. Basaran*
Affiliation:
School of Chemical Engineering, Purdue University, West Lafayette, IN 47907-1283, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Thinning and rupture of a thin film of a power-law fluid on a solid substrate under the balance between destabilizing van der Waals pressure and stabilizing capillary pressure is analysed. In a power-law fluid, viscosity is not constant but is proportional to the deformation rate raised to the 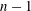$n-1$ power, where 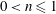$0<n\leqslant 1$ is the power-law exponent (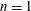$n=1$ for a Newtonian fluid). In the first part of the paper, use is made of the slenderness of the film and the lubrication approximation is applied to the equations of motion to derive a spatially one-dimensional nonlinear evolution equation for film thickness. The variation with time remaining until rupture of the film thickness, the lateral length scale, fluid velocity and viscosity is determined analytically and confirmed by numerical simulations for both line rupture and point rupture. The self-similarity of the numerically computed film profiles in the vicinity of the location where the film thickness is a minimum is demonstrated by rescaling of the transient profiles with the scales deduced from theory. It is then shown that, in contrast to films of Newtonian fluids undergoing rupture for which inertia is always negligible, inertia can become important during thinning of films of power-law fluids in certain situations. The critical conditions for which inertia becomes important and the lubrication approximation is no longer valid are determined analytically. In the second part of the paper, thinning and rupture of thin films of power-law fluids in situations when inertia is important are simulated by solving numerically the spatially two-dimensional, transient Cauchy momentum and continuity equations. It is shown that as such films continue to thin, a change of scaling occurs from a regime in which van der Waals, capillary and viscous forces are important to one where the dominant balance of forces is between van der Waals, capillary and inertial forces while viscous force is negligible.

JFM classification

Interfacial Flows (free surface): Capillary flows Non-Newtonian Flows: Non-Newtonian Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 455 - 483
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajaev, V. S. & Homsy, G. M. 2006 Modeling shapes and dynamics of confined bubbles. Annu. Rev. Fluid Mech. 38, 277–307.Google Scholar
Ambravaneswaran, B., Phillips, S. D. & Basaran, O. A. 2000 Theoretical analysis of a dripping faucet. Phys. Rev. Lett. 85 (25), 5332–5335.Google Scholar
Arora, A. & Doshi, P. 2016 Fingering instability in the flow of a power-law fluid on a rotating disc. Phys. Fluids 28 (1), 013102.CrossRefGoogle Scholar
Barenblatt, G. I. 1996 Scaling, Self-similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics. Cambridge University Press.Google Scholar
Becker, J., Grün, G., Seemann, R., Mantz, H., Jacobs, K., Mecke, K. R. & Blossey, R. 2003 Complex dewetting scenarios captured by thin-film models. Nat. Mater. 2 (1), 59–63.CrossRefGoogle ScholarPubMed
Bhat, P. P., Appathurai, S., Harris, M. T., Pasquali, M., Mckinley, G. H. & Basaran, O. A. 2010 Formation of beads-on-a-string structures during break-up of viscoelastic filaments. Nat. Phys. 6 (8), 625–631.Google Scholar
Bird, R. B., Armstrong, R. C., Hassager, O. & Curtiss, C. F. 1977 Dynamics of Polymeric Liquids. Wiley.Google Scholar
Braun, R. J. 2012 Dynamics of the tear film. Annu. Rev. Fluid Mech. 44, 267–297.Google Scholar
Castrejón-Pita, J. R., Castrejón-Pita, A. A., Thete, S. S., Sambath, K., Hutchings, I. M., Hinch, J., Lister, J. R. & Basaran, O. A. 2015 Plethora of transitions during breakup of liquid filaments. Proc. Natl Acad. Sci. USA 112 (15), 4582–4587.CrossRefGoogle ScholarPubMed
Chen, A. U., Notz, P. K. & Basaran, O. A. 2002 Computational and experimental analysis of pinch-off and scaling. Phys. Rev. Lett. 88 (17), 174501.Google Scholar
Christodoulou, K. N. & Scriven, L. E. 1992 Discretization of free surface flows and other moving boundary problems. J. Comput. Phys. 99 (1), 39–55.CrossRefGoogle Scholar
Cohen-Addad, S., Höhler, R. & Pitois, O. 2013 Flow in foams and flowing foams. Annu. Rev. Fluid Mech. 45 (1), 241–267.Google Scholar
Collins, R. T., Sambath, K., Harris, M. T. & Basaran, O. A. 2013 Universal scaling laws for the disintegration of electrified drops. Proc. Natl Acad. Sci. USA 110 (13), 4905–4910.CrossRefGoogle ScholarPubMed
Dandapat, B. S. & Mukhopadhyay, A. 2003 Waves on the surface of a falling power-law fluid film. Intl J. Non-Linear Mech. 38 (1), 21–38.Google Scholar
De Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.Google Scholar
Deen, W. M. 1998 Analysis of Transport Phenomena. Oxford University Press.Google Scholar
Doshi, P. & Basaran, O. A. 2004 Self-similar pinch-off of power law fluids. Phys. Fluids 16 (3), 585–593.CrossRefGoogle Scholar
Doshi, P., Suryo, R., Yildirim, O. E., McKinley, G. H. & Basaran, O. A. 2003 Scaling in pinch-off of generalized Newtonian fluids. J. Non-Newtonian Fluid Mech. 113 (1), 1–27.Google Scholar
Eggers, J. 1993 Universal pinching of 3d axisymmetric free-surface flow. Phys. Rev. Lett. 71 (21), 3458–3460.CrossRefGoogle ScholarPubMed
Eggers, J. 1997 Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 69 (3), 865–929.Google Scholar
Feng, J. Q. & Basaran, O. A. 1994 Shear-flow over a translationally symmetrical cylindrical bubble pinned on a slot in a plane wall. J. Fluid Mech. 275, 351–378.Google Scholar
Gorla, R. S. R. 2001 Rupture of thin power-law liquid film on a cylinder. J. Appl. Mech. 68 (2), 294–297.Google Scholar
Hasan, S. W., Ghannam, M. T. & Esmail, N. 2010 Heavy crude oil viscosity reduction and rheology for pipeline transportation. Fuel 89 (5), 1095–1100.Google Scholar
Huisman, F. M., Friedman, S. R. & Taborek, P. 2012 Pinch-off dynamics in foams, emulsions and suspensions. Soft Matt. 8 (25), 6767–6774.Google Scholar
Kabov, O. 2000 Breakdown of a liquid film flowing over the surface with a local heat source. Thermophys. Aeromech. 7 (4), 513–520.Google Scholar
Kheshgi, H. S. & Scriven, L. E. 1991 Dewetting: nucleation and growth of dry regions. Chem. Engng Sci. 46 (2), 519–526.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.CrossRefGoogle Scholar
Li, Y. & Sprittles, J. E. 2016 Capillary breakup of a liquid bridge: identifying regimes and transitions. J. Fluid Mech. 797, 29–59.CrossRefGoogle Scholar
Miladinova, S., Lebon, G. & Toshev, E. 2004 Thin-film flow of a power-law liquid falling down an inclined plate. J. Non-Newtonian Fluid Mech. 122 (1), 69–78.Google Scholar
Mitlin, V. S. 1993 Dewetting of solid surface: analogy with spinodal decomposition. J. Colloid. Interface Sci. 156 (2), 491–497.Google Scholar
Munro, J. P., Anthony, C. R., Basaran, O. A. & Lister, J. R. 2015 Thin-sheet flow between coalescing bubbles. J. Fluid Mech. 773, R3.Google Scholar
Nguyen, A. & Schulze, H. J. 2003 Colloidal Science of Flotation. CRC Press.Google Scholar
Notz, P. K. & Basaran, O. A. 2004 Dynamics and breakup of a contracting liquid filament. J. Fluid Mech. 512, 223–256.Google Scholar
Paulsen, J. D., Burton, J. C., Nagel, S. R., Appathuri, S., Harris, M. T. & Basaran, O. A. 2012 The inexorable resistance of inertia determines the initial regime of drop coalescence. Proc. Natl Acad. Sci. USA 109 (18), 6857–6861.CrossRefGoogle ScholarPubMed
Reiter, G. 1992 Dewetting of thin polymer films. Phys. Rev. Lett. 68 (1), 75–78.Google Scholar
Reiter, G., Sharma, A., Casoli, A., David, M., Khanna, R. & Auroy, P. 1999 Thin film instability induced by long-range forces. Langmuir 15 (7), 2551–2558.CrossRefGoogle Scholar
Renardy, M. 2002 Similarity solutions for jet breakup for various models of viscoelastic fluids. J. Non-Newtonian Fluid Mech. 104 (1), 65–74.Google Scholar
Ruckenstein, E. & Jain, R. K. 1974 Spontaneous rupture of thin liquid films. J. Chem. Soc. Faraday Trans. 70, 132–147.Google Scholar
Savage, J. R., Caggioni, M., Spicer, P. T. & Cohen, I. 2010 Partial universality: pinch-off dynamics in fluids with smectic liquid crystalline order. Soft Matt. 6 (5), 892–895.Google Scholar
Stange, T. G., Evans, D. F. & Hendrickson, W. A. 1997 Nucleation and growth of defects leading to dewetting of thin polymer films. Langmuir 13 (16), 4459–4465.Google Scholar
Suryo, R. & Basaran, O. A. 2006 Local dynamics during pinch-off of liquid threads of power law fluids: scaling analysis and self-similarity. J. Non-Newtonian Fluid Mech. 138 (2), 134–160.Google Scholar
Teletzke, G. F., Davis, H. T. & Scriven, L. E. 1987 How liquids spread on solids. Chem. Engng Commun. 55 (1–6), 41–82.Google Scholar
Thete, S. S., Anthony, C., Basaran, O. A. & Doshi, P. 2015 Self-similar rupture of thin free films of power-law fluids. Phys. Rev. E 92 (2), 023014.Google Scholar
Thete, S. S., Anthony, C., Doshi, P., Harris, M. T. & Basaran, O. A. 2016 Self-similarity and scaling transitions during rupture of thin free films of Newtonian fluids. Phys. Fluids 28 (9), 092101.Google Scholar
Timmermans, J. 1960 The Physico-Chemical Constants of Binary Systems in Concentrated Solutions. Interscience.Google Scholar
Vaynblat, D., Lister, J. R. & Witelski, T. P. 2001 Rupture of thin viscous films by van der Waals forces: evolution and self-similarity. Phys. Fluids 13 (5), 1130–1140.CrossRefGoogle Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.Google Scholar
Wilkes, E. D., Phillips, S. D. & Basaran, O. A. 1999 Computational and experimental analysis of dynamics of drop formation. Phys. Fluids 11 (12), 3577–3598.CrossRefGoogle Scholar
Williams, M. B. & Davis, S. H. 1982 Nonlinear theory of film rupture. J. Colloid Interface Sci. 90 (1), 220–228.Google Scholar
Witelski, T. P. & Bernoff, A. J. 1999 Stability of self-similar solutions for van der Waals driven thin film rupture. Phys. Fluids 11 (9), 2443–2445.Google Scholar
Yildirim, O. E. & Basaran, O. A. 2001 Deformation and breakup of stretching bridges of Newtonian and shear-thinning liquids: comparison of one- and two-dimensional models. Chem. Engng Sci. 56 (1), 211–233.Google Scholar
Yildirim, O. E. & Basaran, O. A. 2006 Dynamics of formation and dripping of drops of deformation-rate-thinning and -thickening liquids from capillary tubes. J. Non-Newtonian Fluid Mech. 136 (1), 17–37.Google Scholar
Yoon, Y., Baldessari, F., Ceniceros, H. D. & Leal, L. G. 2007 Coalescence of two equal-sized deformable drops in an axisymmetric flow. Phys. Fluids 19 (10), 102102.CrossRefGoogle Scholar
Zhang, W. W. & Lister, J. R. 1999 Similarity solutions for van der Waals rupture of a thin film on a solid substrate. Phys. Fluids 11 (9), 2454–2462.Google Scholar
Zhang, X., Padgett, R. S. & Basaran, O. A. 1996 Nonlinear deformation and breakup of stretching liquid bridges. J. Fluid Mech. 329, 207–246.Google Scholar
Zhang, Y. L., Matar, O. K. & Craster, R. V. 2003 Analysis of tear film rupture: effect of non-Newtonian rheology. J. Colloid Interface Sci. 262 (1), 130–148.Google Scholar