Article contents
Self-similar kinematics among efficient slender swimmers
Published online by Cambridge University Press: 07 February 2018
Abstract
We present an analysis of efficient undulatory propulsion for slender animals swimming at high Reynolds number. Using Lighthill’s large-amplitude elongated-body theory, we show that optimally efficient swimming kinematics can be characterized through a single dimensionless variable 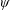 $\unicode[STIX]{x1D713}$. This variable,
$\unicode[STIX]{x1D713}$. This variable, 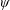 $\unicode[STIX]{x1D713}$, is defined by a simple function of a swimming animal’s body wave properties. Physically,
$\unicode[STIX]{x1D713}$, is defined by a simple function of a swimming animal’s body wave properties. Physically,  $\unicode[STIX]{x1D713}$ characterizes how the velocity of an animal’s tail varies throughout its swimming stroke. Lighthill’s model predicts that swimming efficiency is near optimal in the range
$\unicode[STIX]{x1D713}$ characterizes how the velocity of an animal’s tail varies throughout its swimming stroke. Lighthill’s model predicts that swimming efficiency is near optimal in the range 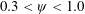 $0.3<\unicode[STIX]{x1D713}<1.0$ and peaks at
$0.3<\unicode[STIX]{x1D713}<1.0$ and peaks at  $\unicode[STIX]{x1D713}=0.87$. At this point, the average magnitude of the tail velocity is minimized and swimming kinematics are tuned such that the thrust coefficient is as close to constant as possible throughout the swimming stroke. We use a compiled dataset of over 250 unique measurements to show that species across a wide range of size and shape fall within the optimal region.
$\unicode[STIX]{x1D713}=0.87$. At this point, the average magnitude of the tail velocity is minimized and swimming kinematics are tuned such that the thrust coefficient is as close to constant as possible throughout the swimming stroke. We use a compiled dataset of over 250 unique measurements to show that species across a wide range of size and shape fall within the optimal region.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 2
- Cited by


