Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Heller, Valentin
2017.
Self-similarity and Reynolds number invariance in Froude modelling.
Journal of Hydraulic Research,
Vol. 55,
Issue. 3,
p.
293.
Kabardin, I.K.
Naumov, I.V.
and
Okulov, V.L.
2017.
An investigation of a self-similarity for local vorticity and velocity components in tip vortex cores of a rotor wake.
Journal of Physics: Conference Series,
Vol. 899,
Issue. ,
p.
022008.
Selçuk, Can
Delbende, Ivan
and
Rossi, Maurice
2017.
Helical vortices: Quasiequilibrium states and their time evolution.
Physical Review Fluids,
Vol. 2,
Issue. 8,
Panossian, Nadia
Herges, Thomas G.
and
Maniaci, David C.
2018.
Wind Turbine Wake Definition and Identification Using Velocity Deficit and Turbulence Profile.
Kabardin, I. K.
Mikkelsen, R. F.
Naumov, I. V.
Okulov, V. L.
Sørensen, J. N.
and
Velte, C. M.
2018.
Self-similarity and helical symmetry of various vortex wakes.
Vol. 2027,
Issue. ,
p.
030115.
Li Gao-Hua
and
Wang Fu-Xin
2018.
Evolution characteristic analysis of double-helical vortex wake of high Reynolds number flow.
Acta Physica Sinica,
Vol. 67,
Issue. 5,
p.
054701.
Okulov, Valery L.
Kabardin, Ivan K.
Mikkelsen, Robert F.
Naumov, Igor V.
and
Sørensen, Jens N.
2019.
Helical self-similarity of tip vortex cores.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
1084.
Okulov, V. L.
and
Fukumoto, Y.
2020.
Analytical solution for self-induced motion of a helical vortex with a Gaussian core.
Thermophysics and Aeromechanics,
Vol. 27,
Issue. 4,
p.
481.
Dierkes, Dominik
Cheviakov, Alexei
and
Oberlack, Martin
2020.
New similarity reductions and exact solutions for helically symmetric viscous flows.
Physics of Fluids,
Vol. 32,
Issue. 5,
Koizumi, Hiroshi
and
Hattori, Yuji
2020.
Structures of wing-tip vortices at low Reynolds numbers and their modelling.
Fluid Dynamics Research,
Vol. 52,
Issue. 4,
p.
045503.
Piqué, A.
Miller, M. A.
and
Hultmark, M.
2022.
Dominant flow features in the wake of a wind turbine at high Reynolds numbers.
Journal of Renewable and Sustainable Energy,
Vol. 14,
Issue. 3,
Xu, Yonghui
Delbende, Ivan
and
Rossi, Maurice
2022.
Quasi-equilibrium states for helical vortices with swirl.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Fakhfekh, Marwa
Ben Amira, Wael
Abid, Malek
and
Maalej, Aref
2023.
Numerical simulations of the wake and deformations of a flexible rotor blade in a turbulent flow.
Physics of Fluids,
Vol. 35,
Issue. 5,
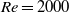 $Re= 2000$ are considered.
$Re= 2000$ are considered.