Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wu, Buchen
Shu, Chang
Lee, HsuChew
and
Wan, Minping
2022.
The effects of caudal fin's bending stiffness on a self-propelled carangiform swimmer.
Physics of Fluids,
Vol. 34,
Issue. 4,
Guvernyuk, S. V.
Dynnikov, Ya. A.
Dynnikova, G. Ya.
and
Malakhova, T. V.
2022.
Hydrodynamic Mechanisms of the Influence of an Elastic Constraint on the Propulsive Force of Airfoil under Semideterministic Oscillations in Viscous Fluid Flow.
Fluid Dynamics,
Vol. 57,
Issue. 5,
p.
549.
Kang, Linlin
Xiong, Shiying
Wu, Buchen
Li, Chao
Ge, Mingming
Yuan, Dehan
Han, Fei
and
Cui, Weicheng
2023.
Force decomposition on flapping flexible plate via impulse theory and dynamic mode decomposition.
Physics of Fluids,
Vol. 35,
Issue. 10,
Xu, MengFan
and
Yu, YongLiang
2023.
Effects of body stiffness on propulsion during fish self-propelled swimming.
Physics of Fluids,
Vol. 35,
Issue. 7,
Luo, Ming
Wu, Zhigang
and
Yang, Chao
2023.
Strongly coupled fluid–structure interaction analysis of aquatic flapping wings based on flexible multibody dynamics and the modified unsteady vortex lattice method.
Ocean Engineering,
Vol. 281,
Issue. ,
p.
114921.
Martínez-Muriel, C.
Arranz, G.
García-Villalba, M.
and
Flores, O.
2023.
Fluid–structure resonance in spanwise-flexible flapping wings.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Kang, Lin-lin
Gong, Shi-xian
Lu, Xi-Yun
Cui, Wei-cheng
and
Fan, Di-xia
2023.
Scaling laws for the intermittent swimming performance of a flexible plate at low Reynolds number.
Journal of Hydrodynamics,
Vol. 35,
Issue. 4,
p.
803.
Jiang, Si-Ying
Yu, Jun
Wang, Jun
Li, Dong-Fang
and
Xu, Yuan-Qing
2023.
A free-swimming tadpole model based on immersed boundary-lattice Boltzmann method and its application.
Physics of Fluids,
Vol. 35,
Issue. 8,
Luo, Ming
Wu, Zhigang
Zhou, Minghao
and
Yang, Chao
2024.
Fluid–Structure Interaction Analysis of Manta-Bots with Self-Induced Vertical Undulations during Fin-Based Locomotion.
Journal of Marine Science and Engineering,
Vol. 12,
Issue. 7,
p.
1165.
Li, Ao
Xu, Du-Chang
and
Xu, Yuan-Qing
2024.
Energy conservation analysis and formation control of multi-tadpoles based on lattice Boltzmann method.
Physics of Fluids,
Vol. 36,
Issue. 8,
Chu, Yong
Gao, Pengcheng
Chen, Xiao
Huang, Qiaogao
Pan, Guang
and
Luo, Yang
2024.
Hydrodynamic performance analysis of swimming processes in self-propelled manta rays.
Physics of Fluids,
Vol. 36,
Issue. 7,
Ji, Xueyu
Jin, Bruce Ruishu
Huang, Qiuxiang
Wang, Li
Ravi, Sridhar
Young, John
Lai, Joseph C.S.
and
Tian, Fang-Bao
2024.
The evolution of vortices determines the aeroacoustics generated by a hovering wing.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Martínez-Muriel, C.
García-Villalba, M.
and
Flores, O.
2024.
On the role of wake-capture and resonance in spanwise-flexible flapping wings in tandem.
Journal of Fluids and Structures,
Vol. 130,
Issue. ,
p.
104175.
Shukla, Sarvesh
Sharma, Atul
Agrawal, Amit
and
Bhardwaj, Rajneesh
2024.
Fish-Inspired Oscillating and/or Undulating Hydrofoil in a Free Stream Flow: A Review on Thrust Generation Mechanisms.
Journal of the Indian Institute of Science,
Vol. 104,
Issue. 1,
p.
147.
Shukla, Sarvesh
Sharma, Atul
Agrawal, Amit
and
Bhardwaj, Rajneesh
2024.
Hydrodynamics and propulsion of a hydrofoil undergoing leading-edge pitching and traveling wave-based surface undulation.
Physics of Fluids,
Vol. 36,
Issue. 4,
Liu, Kui
and
Huang, Haibo
2024.
Wake transition of an unconstrained self-propelled flexible flapping plate.
Physical Review Fluids,
Vol. 9,
Issue. 3,
Liu, Kui
and
Huang, Haibo
2024.
Dynamics of weighted flexible ribbons in a uniform flow.
Journal of Fluid Mechanics,
Vol. 990,
Issue. ,
Zhu, Yi
Kang, Linlin
Tong, Xinyu
Ma, Jingtao
Tian, Fangbao
and
Fan, Dixia
2025.
Intermittent swimmers optimize energy expenditure with flick-to-flick motor control.
Journal of Fluid Mechanics,
Vol. 1006,
Issue. ,
Xu, Mengfan
Zhou, Tianyi
Yu, Yongliang
and
Yin, Bo
2025.
A panel method with resistance correction for a self-propelled bioinspired fish model.
Ocean Engineering,
Vol. 318,
Issue. ,
p.
120105.
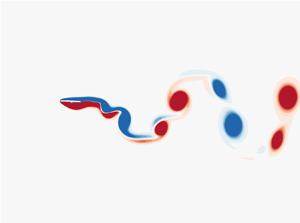
 $U$ (or the cruising Reynolds number
$U$ (or the cruising Reynolds number  $Re_c$), the thrust
$Re_c$), the thrust  $T$ and the input power
$T$ and the input power  $P$ can be summarized as some simple scaling laws vs the flapping Reynolds number
$P$ can be summarized as some simple scaling laws vs the flapping Reynolds number  $Re_f$. In the heaving motion, the scaling laws may be not fully independent of bending stiffness because in the motion the role of bending stiffness is more complicated for the thrust generation. Our scaling laws are well supported by biological data on swimming aquatic animals.
$Re_f$. In the heaving motion, the scaling laws may be not fully independent of bending stiffness because in the motion the role of bending stiffness is more complicated for the thrust generation. Our scaling laws are well supported by biological data on swimming aquatic animals.


