Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Akhavan-Safaei, Ali
Seyedi, S. Hadi
and
Zayernouri, Mohsen
2020.
Anomalous features in internal cylinder flow instabilities subject to uncertain rotational effects.
Physics of Fluids,
Vol. 32,
Issue. 9,
Forooghi, Pourya
Yang, Xiang I. A.
and
Abkar, Mahdi
2020.
Roughness-induced secondary flows in stably stratified turbulent boundary layers.
Physics of Fluids,
Vol. 32,
Issue. 10,
Yang, Xiang I.
Xu, Haosen
and
Milani, Pedro
2021.
Wall-modeled Large-eddy Simulations of Low-speed Flows with Heat Transfer.
Xie, Jin-Han
de Silva, Charitha
Baidya, Rio
Yang, Xiang IA
and
Hu, Ruifeng
2021.
Third-order structure function in the logarithmic layer of boundary-layer turbulence.
Physical Review Fluids,
Vol. 6,
Issue. 7,
Kadivar, Mohammadreza
Tormey, David
and
McGranaghan, Gerard
2021.
A review on turbulent flow over rough surfaces: Fundamentals and theories.
International Journal of Thermofluids,
Vol. 10,
Issue. ,
p.
100077.
Amarloo, Ali
Forooghi, Pourya
and
Abkar, Mahdi
2022.
Frozen propagation of Reynolds force vector from high-fidelity data into Reynolds-averaged simulations of secondary flows.
Physics of Fluids,
Vol. 34,
Issue. 11,
Wang, Yan
Wang, Liang
Jiang, Yao
and
Sun, Xiaojing
2022.
A new method for prediction of power coefficient and wake length of a horizontal axis wind turbine based on energy analysis.
Energy Conversion and Management,
Vol. 252,
Issue. ,
p.
115121.
Mizuno, Yoshinori
Yagi, Toshimasa
and
Mori, Kazuyasu
2022.
Momentum Flux in Turbulent Boundary Layers with Weakly Unstable Stratification.
Journal of the Physical Society of Japan,
Vol. 91,
Issue. 5,
Amarloo, Ali
Forooghi, Pourya
and
Abkar, Mahdi
2022.
Secondary flows in statistically unstable turbulent boundary layers with spanwise heterogeneous roughness.
Theoretical and Applied Mechanics Letters,
Vol. 12,
Issue. 2,
p.
100317.
Yang, Xiang I. A.
Chen, Peng E. S.
Hu, Ruifeng
and
Abkar, Mahdi
2022.
Logarithmic-Linear Law of the Streamwise Velocity Variance in Stably Stratified Boundary Layers.
Boundary-Layer Meteorology,
Vol. 183,
Issue. 2,
p.
199.
Li, Fangbo
Pei, Binbin
and
Bai, Bofeng
2022.
Scaling laws of statistics of wall-bounded turbulence at supercritical pressure: Evaluation and mechanism.
Physics of Fluids,
Vol. 34,
Issue. 8,
Chen, Peng E.S.
Huang, George P.
Shi, Yipeng
Yang, Xiang I.A.
and
Lv, Yu
2022.
A unified temperature transformation for high-Mach-number flows above adiabatic and isothermal walls.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Mataji, Mohammadreza
2022.
On the extension of streamwise turbulence intensity profile beyond the atmospheric surface layer under neutral to unstable stratifications.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 228,
Issue. ,
p.
105100.
Mataji, Mohammadreza
Ashrafi, Khosro
and
Shafie Pour-Motlagh, Majid
2023.
Can wind turbine farms increase settlement of particulate matters during dust events?.
Journal of Renewable and Sustainable Energy,
Vol. 15,
Issue. 1,
Amarloo, Ali
Cinnella, Paola
Iosifidis, Alexandros
Forooghi, Pourya
and
Abkar, Mahdi
2023.
Data-driven Reynolds stress models based on the frozen treatment of Reynolds stress tensor and Reynolds force vector.
Physics of Fluids,
Vol. 35,
Issue. 7,
Mouri, Hideaki
and
Ito, Junshi
2023.
Momentum flux fluctuations in wall turbulence formulated along the distance from the wall.
Physics of Fluids,
Vol. 35,
Issue. 7,
Huang, Haojie
and
Li, Xuebo
2023.
A theoretical model for structure inclination angles in stratified boundary layers: Connecting turbulent scaling and Monin–Obukhov similarity theory.
AIP Advances,
Vol. 13,
Issue. 8,
Vadrot, Aurélien
Yang, Xiang I. A.
Bae, H. Jane
and
Abkar, Mahdi
2023.
Log-law recovery through reinforcement-learning wall model for large eddy simulation.
Physics of Fluids,
Vol. 35,
Issue. 5,
Vadrot, Aurélien
Yang, Xiang I. A.
and
Abkar, Mahdi
2023.
Survey of machine-learning wall models for large-eddy simulation.
Physical Review Fluids,
Vol. 8,
Issue. 6,
Huang, Xinyi L.D.
Kunz, Robert F.
and
Yang, Xiang I.A.
2023.
Linear logistic regression with weight thresholding for flow regime classification of a stratified wake.
Theoretical and Applied Mechanics Letters,
Vol. 13,
Issue. 2,
p.
100414.
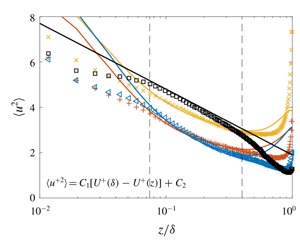
 $L/\unicode[STIX]{x1D6FF}<-0.1$, where
$L/\unicode[STIX]{x1D6FF}<-0.1$, where  $L$ is the Monin–Obukhov length, and
$L$ is the Monin–Obukhov length, and  $\unicode[STIX]{x1D6FF}$ is the boundary-layer height. Reasonably good prediction of velocity fluctuations based on knowledge of the mean velocity profile is obtained.
$\unicode[STIX]{x1D6FF}$ is the boundary-layer height. Reasonably good prediction of velocity fluctuations based on knowledge of the mean velocity profile is obtained.