Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lashermes, B.
Roux, S. G.
Abry, P.
and
Jaffard, S.
2008.
Comprehensive multifractal analysis of turbulent velocity using the wavelet leaders.
The European Physical Journal B,
Vol. 61,
Issue. 2,
p.
201.
Alam, Jahrul M.
and
Lin, John C.
2008.
Toward a Fully Lagrangian Atmospheric Modeling System.
Monthly Weather Review,
Vol. 136,
Issue. 12,
p.
4653.
Mehra, Mani
and
Kevlahan, Nicholas K.-R.
2008.
An adaptive wavelet collocation method for the solution of partial differential equations on the sphere.
Journal of Computational Physics,
Vol. 227,
Issue. 11,
p.
5610.
Kevlahan, Nicholas
2009.
150 Years of Vortex Dynamics.
Vol. 20,
Issue. ,
p.
257.
Regele, J. D.
and
Vasilyev, O. V.
2009.
An adaptive wavelet-collocation method for shock computations.
International Journal of Computational Fluid Dynamics,
Vol. 23,
Issue. 7,
p.
503.
Kevlahan, Nicholas
2010.
Vortices for computing: the engines of turbulence simulation.
Theoretical and Computational Fluid Dynamics,
Vol. 24,
Issue. 1-4,
p.
241.
DE STEFANO, G.
and
VASILYEV, O. V.
2010.
Stochastic coherent adaptive large eddy simulation of forced isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 646,
Issue. ,
p.
453.
Schneider, Kai
and
Vasilyev, Oleg V.
2010.
Wavelet Methods in Computational Fluid Dynamics.
Annual Review of Fluid Mechanics,
Vol. 42,
Issue. 1,
p.
473.
Alam, Jahrul M.
2011.
Toward a Multiscale Approach for Computational Atmospheric Modeling.
Monthly Weather Review,
Vol. 139,
Issue. 12,
p.
3906.
Nguyen van yen, Romain
Farge, Marie
and
Schneider, Kai
2012.
Scale-wise coherent vorticity extraction for conditional statistical modeling of homogeneous isotropic two-dimensional turbulence.
Physica D: Nonlinear Phenomena,
Vol. 241,
Issue. 3,
p.
186.
Alam, Jahrul M.
Kevlahan, Nicholas K.-R.
Vasilyev, Oleg V.
and
Hossain, Zahangir
2012.
A Multiresolution Model for the Simulation of Transient Heat and Mass Transfer.
Numerical Heat Transfer, Part B: Fundamentals,
Vol. 61,
Issue. 3,
p.
147.
Pudritz, Ralph E.
and
Kevlahan, N. K.-R.
2013.
Shock interactions, turbulence and the origin of the stellar mass spectrum.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 371,
Issue. 2003,
p.
20120248.
Nejadmalayeri, Alireza
Vezolainen, Alexei
and
Vasilyev, Oleg V.
2013.
Reynolds number scaling of coherent vortex simulation and stochastic coherent adaptive large eddy simulation.
Physics of Fluids,
Vol. 25,
Issue. 11,
San, Omer
and
Staples, Anne E.
2013.
Stationary two-dimensional turbulence statistics using a Markovian forcing scheme.
Computers & Fluids,
Vol. 71,
Issue. ,
p.
1.
Dubos, T.
and
Kevlahan, N. K‐R.
2013.
A conservative adaptive wavelet method for the shallow‐water equations on staggered grids.
Quarterly Journal of the Royal Meteorological Society,
Vol. 139,
Issue. 677,
p.
1997.
Alam, Jahrul
and
Islam, Mo Rokibul
2014.
A multiscale eddy simulation methodology for the atmospheric Ekman boundary layer.
Geophysical & Astrophysical Fluid Dynamics,
p.
1.
Nejadmalayeri, Alireza
Vezolainen, Alexei
De Stefano, Giuliano
and
Vasilyev, Oleg V.
2014.
Fully adaptive turbulence simulations based on Lagrangian spatio-temporally varying wavelet thresholding.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
794.
De Stefano, Giuliano
and
Vasilyev, Oleg V.
2014.
Wavelet-based adaptive simulations of three-dimensional flow past a square cylinder.
Journal of Fluid Mechanics,
Vol. 748,
Issue. ,
p.
433.
Reckinger, Shanon M.
Vasilyev, Oleg V.
and
Fox-Kemper, Baylor
2014.
Adaptive wavelet collocation method on the shallow water model.
Journal of Computational Physics,
Vol. 271,
Issue. ,
p.
342.
Nejadmalayeri, Alireza
Vezolainen, Alexei
Brown-Dymkoski, Eric
and
Vasilyev, Oleg V.
2015.
Parallel adaptive wavelet collocation method for PDEs.
Journal of Computational Physics,
Vol. 298,
Issue. ,
p.
237.
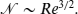 . These bounds neglect intermittency, and it is not known how sharp they are. In this paper we use an adaptive multi-scale wavelet collocation method to estimate for the first time the number of space–time computational modes
. These bounds neglect intermittency, and it is not known how sharp they are. In this paper we use an adaptive multi-scale wavelet collocation method to estimate for the first time the number of space–time computational modes  necessary to represent two-dimensional decaying turbulence as a function of Reynolds number. We find that
necessary to represent two-dimensional decaying turbulence as a function of Reynolds number. We find that 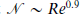 for 1260 ≤ Re ≤ 40400 over many eddy turn-over times, and that temporal intermittency is stronger than spatial intermittency. The spatial modes alone scale like Re0.7. The β-model then implies that the spatial fractal dimension of the active regions is 1.2, and the temporal fractal dimension is 0.3. These results suggest that the usual estimates are not sharp for adaptive numerical simulations. The relatively high compression confirms the importance of intermittency and encourages the search for reduced mathematical models of two-dimensional turbulence (e.g. in terms of coherent vortices).
for 1260 ≤ Re ≤ 40400 over many eddy turn-over times, and that temporal intermittency is stronger than spatial intermittency. The spatial modes alone scale like Re0.7. The β-model then implies that the spatial fractal dimension of the active regions is 1.2, and the temporal fractal dimension is 0.3. These results suggest that the usual estimates are not sharp for adaptive numerical simulations. The relatively high compression confirms the importance of intermittency and encourages the search for reduced mathematical models of two-dimensional turbulence (e.g. in terms of coherent vortices).