Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T23:56:23.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling laws for mixing and dissipation in unforced rotating stratified turbulence

Published online by Cambridge University Press:  06 April 2018

A. Pouquet Open the ORCID record for A. Pouquet [Opens in a new window] ,
D. Rosenberg ,
R. Marino  and
C. Herbert
A. Pouquet*
Affiliation:
National Center for Atmospheric Research, P.O. Box 3000, Boulder, CO 80307, USA Laboratory for Atmospheric and Space Physics, University of Colorado, Boulder, CO 80309, USA
D. Rosenberg
Affiliation:
1401 Bradley Drive, Boulder, CO 80305, USA
R. Marino
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS, École Centrale de Lyon, Université de Lyon, INSA de Lyon Écully, 69134, France
C. Herbert
Affiliation:
Univ Lyon, ENS de Lyon, Univ Claude Bernard, CNRS, Laboratoire de Physique, F-69342 Lyon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a model for the scaling of mixing in weakly rotating stratified flows characterized by their Rossby, Froude and Reynolds numbers 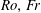$Ro,Fr$, 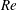$Re$. This model is based on quasi-equipartition between kinetic and potential modes, sub-dominant vertical velocity, 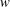$w$, and lessening of the energy transfer to small scales as measured by a dissipation efficiency 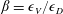$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D716}_{V}/\unicode[STIX]{x1D716}_{D}$, with 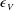$\unicode[STIX]{x1D716}_{V}$ the kinetic energy dissipation and 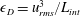$\unicode[STIX]{x1D716}_{D}=u_{rms}^{3}/L_{int}$ its dimensional expression, with 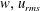$w,u_{rms}$ the vertical and root mean square velocities, and 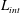$L_{int}$ the integral scale. We determine the domains of validity of such laws for a large numerical study of the unforced Boussinesq equations mostly on grids of 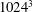$1024^{3}$ points, with 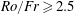$Ro/Fr\geqslant 2.5$, and with 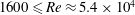$1600\leqslant Re\approx 5.4\times 10^{4}$; the Prandtl number is one, initial conditions are either isotropic and at large scale for the velocity and zero for the temperature 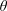$\unicode[STIX]{x1D703}$, or in geostrophic balance. Three regimes in Froude number, as for stratified flows, are observed: dominant waves, eddy–wave interactions and strong turbulence. A wave–turbulence balance for the transfer time 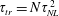$\unicode[STIX]{x1D70F}_{tr}=N\unicode[STIX]{x1D70F}_{NL}^{2}$, with 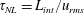$\unicode[STIX]{x1D70F}_{NL}=L_{int}/u_{rms}$ the turnover time and 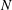$N$ the Brunt–Väisälä frequency, leads to 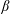$\unicode[STIX]{x1D6FD}$ growing linearly with 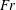$Fr$ in the intermediate regime, with a saturation at 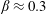$\unicode[STIX]{x1D6FD}\approx 0.3$ or more, depending on initial conditions for larger Froude numbers. The Ellison scale is also found to scale linearly with 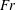$Fr$. The flux Richardson number 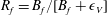$R_{f}=B_{f}/[B_{f}+\unicode[STIX]{x1D716}_{V}]$, with 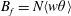$B_{f}=N\langle w\unicode[STIX]{x1D703}\rangle$ the buoyancy flux, transitions for approximately the same parameter values as for 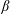$\unicode[STIX]{x1D6FD}$. These regimes for the present study are delimited by 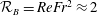${\mathcal{R}}_{B}=ReFr^{2}\approx 2$ and 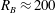$R_{B}\approx 200$. With 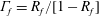$\unicode[STIX]{x1D6E4}_{f}=R_{f}/[1-R_{f}]$ the mixing efficiency, putting together the three relationships of the model allows for the prediction of the scaling 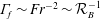$\unicode[STIX]{x1D6E4}_{f}\sim Fr^{-2}\sim {\mathcal{R}}_{B}^{-1}$ in the low and intermediate regimes for high 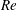$Re$, whereas for higher Froude numbers, 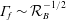$\unicode[STIX]{x1D6E4}_{f}\sim {\mathcal{R}}_{B}^{-1/2}$, a scaling already found in observations: as turbulence strengthens, 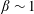$\unicode[STIX]{x1D6FD}\sim 1$, 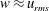$w\approx u_{rms}$, and smaller buoyancy fluxes together correspond to a decoupling of velocity and temperature fluctuations, the latter becoming passive.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 519 - 545
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barry, M., Ivey, G., Winters, K. & Imberger, J. 2001 Measurements of diapycnal diffusivities in stratified fluids. J. Fluid Mech. 442, 267–291.10.1017/S0022112001005080Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascade in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.10.1175/1520-0469(1995)052<4410:GAAICI>2.0.CO;22.0.CO;2>Google Scholar
Billant, P. & Chomaz, J. M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.10.1063/1.1369125Google Scholar
Bluteau, C. E., Jones, N. L. & Ivey, G. N. 2013 Turbulent mixing efficiency at an energetic ocean site. J. Geophys. Res. 118, 1–11.10.1002/jgrc.20292Google Scholar
van Bokhoven, L. J. A., Clercx, H. J. H., van Heijst, G. J. F. & Trieling, R. R. 2009 Experiments on rapidly rotating turbulent flows. Phys. Fluids 21, 096601.10.1063/1.3197876Google Scholar
Bouffard, D. & Boegman, L. 2013 A diapycnal diffusivity model for stratified environmental flows. Dyn. Atmos. Oceans 61–62, 14–34.10.1016/j.dynatmoce.2013.02.002Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J. M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.10.1017/S0022112007006854Google Scholar
de Bruyn Kops, S. M. 2015 Classical scaling and intermittency in strongly stratifed Boussinesq turbulence. J. Fluid Mech. 775, 436–463.10.1017/jfm.2015.274Google Scholar
Cambon, C., Godeferd, F. S., Nicolleau, F. & Vassilicos, J. C. 2004 Turbulent diffusion in rapidly rotating flows with and without stable stratification. J. Fluid Mech. 499, 231–255.10.1017/S0022112003007055Google Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.10.1017/S0022112089001199Google Scholar
D’Asaro, E., Lee, C., Rainville, L., Harcourt, R. & Thomas, L. 2011 Enhanced turbulence and energy dissipation at ocean fronts. Science 332, 318–322.10.1126/science.1201515Google Scholar
Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.10.1017/S0022112006009827Google Scholar
Davis, K. A. & Monismith, S. G. 2011 The modification of bottom boundary layer turbulence and mixing by internal waves shoaling on a barrier reef. J. Phys. Oceanogr. 41, 2223–2241.10.1175/2011JPO4344.1Google Scholar
de Lavergne, C., Madec, G., Le Sommier, J., Nurser, A. J. G. & Garabato, A. C. Naveira 2016 The impact of a variable mixing efficiency on the abyssal overturning. J. Phys. Ocean. 46, 663–681.10.1175/JPO-D-14-0259.1Google Scholar
Dillon, T. M. 1982 Vertical overturns: A comparison of Thorpe and Ozmidov length scales. J. Geophys. Res. 87, 9601–9613.10.1029/JC087iC12p09601Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.10.1146/annurev.fluid.36.050802.122015Google Scholar
Dritschel, D. G. & McKiver, W. J. 2015 Effect of Prandtl’s ratio in geophysical turbulence. J. Fluid Mech. 777, 569–590.10.1017/jfm.2015.348Google Scholar
Ferrari, R., Mashayek, A., McDougall, T. J., Nikurashin, M. & Campin, J. M. 2016 Turning ocean mixing upside down. J. Phys. Oceanogr. 46, 2239–2261.10.1175/JPO-D-15-0244.1Google Scholar
Finnigan, J. 1999 A note on wave-turbulence interactions and the possibility of scaling the very stable planetary boundary layer. Boundary-Layer Meteorol. 90, 529–539.10.1023/A:1001756912935Google Scholar
Fleury, M. & Lueck, R. G. 1994 Direct heat flux estimates using a towed vehicle. J. Phys. Oceangr. 24, 801–818.10.1175/1520-0485(1994)024<0801:DHFEUA>2.0.CO;22.0.CO;2>Google Scholar
van Haren, H., Cimatoribus, A. A., Cyr, F. & Gostiaux, L. 2016 Insights from a 3-D temperature sensors mooring on stratified ocean turbulence. Geophys. Res. Lett. 43, 1–7.10.1002/2016GL068032Google Scholar
Herbert, C., Marino, R., Pouquet, A. & Rosenberg, D. 2016 Waves and vortices in the inverse cascade regime of rotating stratified turbulence with or without rotation. J. Fluid Mech. 806, 165–204.10.1017/jfm.2016.581Google Scholar
Herring, J. R. 1980 Statistical theory of quasi-geostrophic turbulence. J. Atmos. Sci. 37, 969–977.10.1175/1520-0469(1980)037<0969:RDOWTS>2.0.CO;22.0.CO;2>Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.10.1146/annurev.fluid.010908.165203Google Scholar
Ivey, G., Winters, K. & Koseff, J. 2008 Density stratification, turbulence but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.10.1146/annurev.fluid.39.050905.110314Google Scholar
Iyer, K. P., Sreenivasan, K. R. & Yeung, P. K. 2017 Reynolds number scaling of velocity increments in isotropic turbulence. Phys. Rev. E 95, 021101(R).Google Scholar
Karimpour, F. & Venayagamoorthy, S. K. 2015 On turbulent mixing in stably stratified wall-bounded flows. Phys. Fluids 27, 046603.10.1063/1.4918533Google Scholar
Kimura, Y. & Herring, J. R. 1996 Diffusion in stably stratified turbulence. J. Fluid Mech. 328, 253–269.10.1017/S0022112096008713Google Scholar
Klymak, J. M., Pinkel, R. & Rainville, L. 2008 Direct breaking of the internal tide near topography: Kaena Ridge, Hawaii. J. Phys. Oceanogr. 38, 380–399.10.1175/2007JPO3728.1Google Scholar
Kurien, S. & Smith, L. M. 2014 Effect of rotation and domain aspect-ratio on layer formation in strongly stratified Boussinesq flows. J. Turbul. 15, 241–271.10.1080/14685248.2014.895832Google Scholar
Laval, J.-P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: Successive transitions with reynolds number. Phys. Rev. E 68, 036308.Google Scholar
Lelong, M.-P. & Riley, J. J. 1991 Internal wave-vortical mode interactions in strongly stratified flows. J. Fluid Mech. 232, 1–19.10.1017/S0022112091003609Google Scholar
Lelong, M.-P. & Sundermeyer, M. 2005 Geostrophic adjustment of an isolated diapycnal mixing event and its implications for small-scale lateral dispersion. J. Phys. Oceanogr. 35, 2352–2367.10.1175/JPO2835.1Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.10.1017/S0022112005008128Google Scholar
Lindborg, E. & Brethouwer, G. 2008 Vertical dispersion by stratified turbulence. J. Fluid Mech. 614, 303–314.10.1017/S0022112008003595Google Scholar
Liu, H. L., Yudin, V. & Roble, R. 2013 Day-to-day ionospheric variability due to lower atmosphere perturbations. Geophys. Res. Lett. 40, 665–670.10.1002/grl.50125Google Scholar
Lozovatsky, I. D. & Fernando, H. J. S. 2013 Mixing efficiency in natural flows. Phil. Trans. R. Soc. Lond. A 371, 20120213.10.1098/rsta.2012.0213Google Scholar
Luketina, D. & Imberger, J. 1989 Turbulence and entrainment in a buoyant surface plume. J. Geophys. Res. 94, 12619–12636.10.1029/JC094iC09p12619Google Scholar
Maffioli, A., Brethouwer, G. & Lindborg, E. 2016 Mixing efficiency in stratified turbulence. J. Fluid Mech. 794, R3.10.1017/jfm.2016.206Google Scholar
Maffioli, A. & Davidson, P. A. 2016 Dynamics of stratified turbulence decaying from a high buoyancy Reynolds number. J. Fluid Mech. 786, 210–233.10.1017/jfm.2015.667Google Scholar
Marino, R., Pouquet, A. & Rosenberg, D. 2015a Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 114, 114504.10.1103/PhysRevLett.114.114504Google Scholar
Marino, R., Rosenberg, D., Herbert, C. & Pouquet, A. 2015b Interplay of waves and eddies in rotating stratified turbulence and the link with kinetic-potential energy partition. Eur. Phys. Lett. 112, 49001.10.1209/0295-5075/112/49001Google Scholar
Mashayek, A. & Peltier, W. R. 2013 Shear-induced mixing in geophysical flows: does the route to turbulence matter to its efficiency? J. Fluid Mech. 725, 216–261.10.1017/jfm.2013.176Google Scholar
Mashayek, A., Salehipour, H., Bouffard, D., Caulfield, C. P., Ferrari, R., Nikurashin, M., Peltier, W. R. & Smyth, W. D. 2017 Efficiency of turbulent mixing in the abyssal ocean circulation. Geophys. Res. Lett. 44, 6296–6306.10.1002/2016GL072452Google Scholar
Mater, B. D., Schaad, S. M. & Venayagamoorthy, S. K. 2013 Relevance of the Thorpe length scale in stably stratified turbulence. Phys. Fluids 25, 076604.10.1063/1.4813809Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014 The quest for an unambiguous parameterization of mixing efficiency in stably stratified geophysical flows. Geophys. Res. Lett. 41, 4646–4653.10.1002/2014GL060571Google Scholar
McWilliams, J. 2016 Submesoscale currents in the ocean. Proc. R. Soc. Lond. A 472, 2016.0117.10.1098/rspa.2016.0117Google Scholar
Métais, O. & Herring, J. 1989 Numerical simulations of freely evolving turbulence in stably stratified fluids. J. Fluid Mech. 202, 117–148.10.1017/S0022112089001126Google Scholar
Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Isotropization at small scale of rotating helically driven turbulence. J. Fluid Mech. 699, 263–279.10.1017/jfm.2012.99Google Scholar
Mininni, P. D., Rosenberg, D., Reddy, R. & Pouquet, A. 2011 A hybrid MPI-OpenMP scheme for scalable parallel pseudospectral computations for fluid turbulence. Parallel Comput. 37, 316–326.10.1016/j.parco.2011.05.004Google Scholar
Monin, A. S. & Yaglom, A. M. 1979 Statistical Fluid Mechanics. MIT Press, Cambridge.Google Scholar
Oks, D., Mininni, P. D. & Pouquet, A.2018 Generation of turbulence through frontogenesis in sheared stratified flows. Phys. Fluids (submitted) arXiv:1706.10287v2.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.10.1175/1520-0485(1980)010<0083:EOTLRO>2.0.CO;22.0.CO;2>Google Scholar
Paoli, R., Thouron, O., Escobar, J., Picot, J. & Cariolle, D. 2014 High-resolution large-eddy simulations of stably stratified flows: application to subkilometer-scale turbulence in the upper troposphere–lower stratosphere. Atm. Chem. Phys. 14, 5037–5055.10.5194/acp-14-5037-2014Google Scholar
Patterson, M. D., Caulfield, C. P., McElwaine, J. N. & Dalziel, S. B. 2006 Time-dependent mixing in stratified Kelvin–Helmholtz billows: Experimental observations. Geophys. Res. Lett. 33, L15608.10.1029/2006GL026949Google Scholar
Peltier, W. & Caulfield, C. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.10.1146/annurev.fluid.35.101101.161144Google Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid: Is it unstable? Deep-Sea Res. 19, 79–81.Google Scholar
Pouquet, A. & Marino, R. 2013 Geophysical turbulence and the duality of the energy flow across scales. Phys. Rev. Lett. 111, 234501.10.1103/PhysRevLett.111.234501Google Scholar
Pouquet, A., Marino, R., Mininni, P. D. & Rosenberg, D. 2017 Dual constant-flux energy cascades to both large scales and small scales. Phys. Fluids 29, 111108.10.1063/1.5000730Google Scholar
Praud, O., Sommeria, J. & Fincham, A. 2006 Decaying grid turbulence in a rotating stratified fluid. J. Fluid Mech. 547, 389–412.10.1017/S0022112005007068Google Scholar
Pumir, A., Xu, H. & Siggia, E. D. 2016 Small-scale anisotropy in turbulent boundary layers. J. Fluid Mech. 804, 5–23.10.1017/jfm.2016.529Google Scholar
Riley, J. J. & deBruynKops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.10.1063/1.1578077Google Scholar
Rorai, C., Mininni, P. D. & Pouquet, A. 2014 Turbulence comes in bursts in stably stratified flows. Phys. Rev. E 89, 043002.Google Scholar
Rosenberg, D., Marino, R., Herbert, C. & Pouquet, A. 2016 Variations of characteristic time-scales in rotating stratified turbulence using a large parametric numerical study. Eur. Phys. J. E 39, 8.Google Scholar
Rosenberg, D., Marino, R., Herbert, C. & Pouquet, A. 2017 Correction to: Variations of characteristic time scales in rotating stratified turbulence using a large parametric numerical study. Eur. Phys. J. E 40, 87.Google Scholar
Rosenberg, D., Pouquet, A., Marino, R. & Mininni, P. D. 2015 Evidence for Bolgiano–Obukhov scaling in rotating stratified turbulence using high-resolution direct numerical simulations. Phys. Fluids 27, 055105.10.1063/1.4921076Google Scholar
Rubinstein, R., Clark, T. T. & Kurien, S. 2017 Leith diffusion model for homogeneous anisotropic turbulence. Comput. Fluids 151, 108–114.10.1016/j.compfluid.2016.07.009Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.10.1017/jfm.2015.305Google Scholar
Shih, L., Koseff, J., Ivey, G. & Ferziger, J. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.10.1017/S0022112004002587Google Scholar
Smyth, W. D., Moum, J. N. & Caldwell, D. R. 2001 The efficiency of mixing in turbulent patches: Inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31, 1969–1992.10.1175/1520-0485(2001)031<1969:TEOMIT>2.0.CO;22.0.CO;2>Google Scholar
Sozza, A., Boffetta, G., Muratore-Ginanneschi, P. & Musacchio, S. 2015 Dimensional transition of energy cascades in stably stratified forced thin fluid layers. Phys. Fluids 27, 035112.10.1063/1.4915074Google Scholar
Stacey, M., Monismith, S. & Burau, J. 1999 Observations of turbulence in a partially stratified estuary. J. Phys. Oceanogr. 29, 1950–1970.10.1175/1520-0485(1999)029<1950:OOTIAP>2.0.CO;22.0.CO;2>Google Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: From instabilities to turbulence. Annu. Rev. Fluid Mech. 34, 559–593.10.1146/annurev.fluid.34.090601.130953Google Scholar
Stillinger, D., Helland, K. & van Atta, C. 1983 Experiments on the transition of homogeneous turbulence to internal waves in a stratified fluid. J. Fluid Mech. 131, 91–122.10.1017/S0022112083001251Google Scholar
Stretch, D. D., Rottman, J., Venayagamoorthy, S. K., Nomura, K. & Rehmann, C. R. 2010 Mixing efficiency in decaying stably stratified turbulence. Dyn. Atmos. Oceans 49, 25–36.10.1016/j.dynatmoce.2008.11.002Google Scholar
Sukoriansky, S., Galperin, B. & Staroselsky, I. 2005 A quasinormal scale elimination model of turbulent flows with stable stratification. Phys. Fluids 17, 085107.10.1063/1.2009010Google Scholar
Thorpe, S. A. 1987 Transitional phenomena and the development of turbulence in stratified fluids: a review. J. Geophys. Res. 92, 5231–5248.10.1029/JC092iC05p05231Google Scholar
Venayagamoorthy, S. K. & Koseff, J. R. 2016 On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 798, R1–R10.10.1017/jfm.2016.340Google Scholar
Waite, M. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.10.1017/S0022112006002060Google Scholar
Wells, M., Cenedese, C. & Caulfield, C. P. 2010 The relationship between flux coefficient and entrainment ratio in density currents. J. Phys. Oceanogr. 40, 2713–2727.10.1175/2010JPO4225.1Google Scholar
Zakharov, V. E., L’vov, V. S. & Falkovich, G. 1992 Kolmogorov spectra of turbulence: Wave turbulence. In Non-Linear Dynamics, Springer.Google Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Rogachevskii, I. & Esau, I. 2013 A hierarchy of energy- and flux-budget (EFB) turbulence closure models for stably-stratified geophysical flows. Boundary-Layer Meteorol. 146, 341–373.10.1007/s10546-012-9768-8Google Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Rogachevskii, I., Esau, I., Mauritsen, T. & Miles, M. W. 2008 Turbulence energetics in stably stratified geophysical flows: Strong and weak mixing regimes. Q. J. R. Meteorol. Soc. 134, 793–799.10.1002/qj.264Google Scholar