Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-04T21:22:33.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling laws for jets of single cavitation bubbles

Published online by Cambridge University Press:  03 August 2016

Outi Supponen Open the ORCID record for Outi Supponen [Opens in a new window] ,
Danail Obreschkow ,
Marc Tinguely ,
Philippe Kobel ,
Nicolas Dorsaz  and
Mohamed Farhat Open the ORCID record for Mohamed Farhat [Opens in a new window]
Outi Supponen*
Affiliation:
Laboratory for Hydraulic Machines, Ecole Polytechnique Fédérale de Lausanne, Avenue de Cour 33 Bis, 1007 Lausanne, Switzerland
Danail Obreschkow
Affiliation:
International Centre for Radio Astronomy Research, University of Western Australia, 7 Fairway, Crawley, WA 6009, Australia
Marc Tinguely
Affiliation:
Laboratory for Hydraulic Machines, Ecole Polytechnique Fédérale de Lausanne, Avenue de Cour 33 Bis, 1007 Lausanne, Switzerland
Philippe Kobel
Affiliation:
Laboratory for Hydraulic Machines, Ecole Polytechnique Fédérale de Lausanne, Avenue de Cour 33 Bis, 1007 Lausanne, Switzerland
Nicolas Dorsaz
Affiliation:
Laboratory for Hydraulic Machines, Ecole Polytechnique Fédérale de Lausanne, Avenue de Cour 33 Bis, 1007 Lausanne, Switzerland
Mohamed Farhat
Affiliation:
Laboratory for Hydraulic Machines, Ecole Polytechnique Fédérale de Lausanne, Avenue de Cour 33 Bis, 1007 Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fast liquid jets, called micro-jets, are produced within cavitation bubbles experiencing an aspherical collapse. Here we review micro-jets of different origins, scales and appearances, and propose a unified framework to describe their dynamics by using an anisotropy parameter 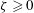$\unicode[STIX]{x1D701}\geqslant 0$, representing a dimensionless measure of the liquid momentum at the collapse point (Kelvin impulse). This parameter is rigorously defined for various jet drivers, including gravity and nearby boundaries. Combining theoretical considerations with hundreds of high-speed visualisations of bubbles collapsing near a rigid surface, near a free surface or in variable gravity, we classify the jets into three distinct regimes: weak, intermediate and strong. Weak jets (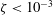$\unicode[STIX]{x1D701}<10^{-3}$) hardly pierce the bubble, but remain within it throughout the collapse and rebound. Intermediate jets (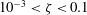$10^{-3}<\unicode[STIX]{x1D701}<0.1$) pierce the opposite bubble wall close to the last collapse phase and clearly emerge during the rebound. Strong jets (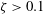$\unicode[STIX]{x1D701}>0.1$) pierce the bubble early during the collapse. The dynamics of the jets is analysed through key observables, such as the jet impact time, jet speed, bubble displacement, bubble volume at jet impact and vapour-jet volume. We find that, upon normalising these observables to dimensionless jet parameters, they all reduce to straightforward functions of $\unicode[STIX]{x1D701}$, which we can reproduce numerically using potential flow theory. An interesting consequence of this result is that a measurement of a single observable, such as the bubble displacement, suffices to estimate any other parameter, such as the jet speed. Remarkably, the dimensionless parameters of intermediate and weak jets (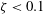$\unicode[STIX]{x1D701}<0.1$) depend only on 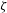$\unicode[STIX]{x1D701}$, not on the jet driver (i.e. gravity or boundaries). In the same regime, the jet parameters are found to be well approximated by power laws of 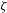$\unicode[STIX]{x1D701}$, which we explain through analytical arguments.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Cavitation Drops and Bubbles: Drops and Bubbles
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 263 - 293
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arndt, R. E. A. 1981 Cavitation in fluid machinery and hydraulic structures. Annu. Rev. Fluid Mech. 13, 273–328.CrossRefGoogle Scholar
Benjamin, T. B. & Ellis, A. T. 1966 The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Phil. Trans. R. Soc. Lond. 260, 221–240.Google Scholar
Blake, J. R. 1988 The Kelvin impulse: application to cavitation bubble dynamics. J. Austral. Math. Soc. B 30, 127–146.Google Scholar
Blake, J. R. & Gibson, D. C. 1987 Cavitation bubbles near boundaries. Annu. Rev. Fluid Mech. 19, 99–123.CrossRefGoogle Scholar
Blake, J. R., Leppinen, D. M. & Wang, Q. 2015 Cavitation and bubble dynamics: the Kelvin impulse and its applications. Interface Focus 5, 20150017.Google Scholar
Brujan, E. A., Ikeda, T. & Matsumoto, Y. 2005 Jet formation and shock wave emission during collapse of ultrasound-induced cavitation bubbles and their role in the therapeutic applications of high-intensity focused ultrasound. Phys. Med. Biol. 50 (20), 4797.CrossRefGoogle ScholarPubMed
Brujan, E.-A., Keen, G. S., Vogel, A. & Blake, J. R. 2002 The final stage of the collapse of a cavitation bubble close to a rigid boundary. Phys. Fluids 14 (1), 85–92.CrossRefGoogle Scholar
Brujan, E.-A., Nahen, K., Schmidt, P. & Vogel, A. 2001a Dynamics of laser-induced cavitation bubbles near elastic boundaries: influence of the elastic modulus. J. Fluid Mech. 433, 283–314.CrossRefGoogle Scholar
Brujan, E.-A., Nahen, K., Schmidt, P. & Vogel, A. 2001b Dynamics of laser-induced cavitation bubbles near an elastic boundary. J. Fluid Mech. 433, 251–281.CrossRefGoogle Scholar
Chahine, G. L. & Bovis, A. 1980 Oscillation and collapse of a cavitation bubble in the vicinity of a two-liquid interface. In Cavitation and Inhomogeneities in Underwater Acoustics, Springer Series in Electrophysics, vol. 4, pp. 23–29. Springer.CrossRefGoogle Scholar
Chanine, G. L. & Genoux, P. F. 1983 Collapse of a cavitating vortex ring. J. Fluids Engng 105, 400–405.CrossRefGoogle Scholar
Dijkink, R. & Ohl, C.-D. 2008 Laser-induced cavitation based micropump. Lab on a Chip 8, 1676–1681.CrossRefGoogle ScholarPubMed
Gerold, B., Glynne-Jones, P., McDougall, C., McGloin, D., Cochran, S., Melzer, A. & Prentice, P. 2012 Directed jetting from collapsing cavities exposed to focused ultrasound. Appl. Phys. Lett. 100 (2), 024104.CrossRefGoogle Scholar
Gibson, D. C.1968 Cavitation adjacent to plane boundaries. Third Australasian Conference on Hydraulics and Fluid Mechanics, Sydney, 25–29 November 1968, Paper 2597. The Institution of Engineers, Australia.Google Scholar
Gibson, D. C. & Blake, J. R. 1982 The growth and collapse of bubbles near deformable surfaces. Appl. Sci. Res. 38, 215–224.Google Scholar
Gregorčič, P., Petkovšek, R. & Možina, J. 2007 Investigation of a cavitation bubble between a rigid boundary and a free surface. J. Appl. Phys. 102, 094904.Google Scholar
Hung, C. F. & Hwangfu, J. J. 2010 Experimental study of the behaviour of mini-charge underwater explosion bubbles near different boundaries. J. Fluid Mech. 651, 55–80.Google Scholar
Klaseboer, E., Hung, K. C., Wang, C., Wang, C. W., Khoo, B. C., Boyce, P., Debono, S. & Charlier, H. 2005 Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 537, 387–413.CrossRefGoogle Scholar
Kobel, P., Obreschkow, D., de Bosset, A., Dorsaz, N. & Farhat, M. 2009 Techniques for generating centimetric drops in microgravity and application to cavitation studies. Exp. Fluids 47, 39–48.Google Scholar
Lauterborn, W. 1982 Cavitation bubble dynamics – new tools for an intricate problem. Appl. Sci. Res. 38, 165–178.Google Scholar
Lauterborn, W. & Kurz, T. 2010 Physics of bubble oscillations. Rep. Prog. Phys. 73 (10), 106501.Google Scholar
Lauterborn, W. & Ohl, C.-D. 1997 Cavitation bubble dynamics. Ultrason. Sonochem. 4, 65–75.CrossRefGoogle ScholarPubMed
Levkovskii, Y. L. & II’in, V. P. 1968 Effect of surface tension and viscosity on the collapse of a cavitation bubble. Inzhenerno-Fizicheskii Zh. 14 (5), 478–480.Google Scholar
Lindau, O. & Lauterborn, W. 2004 Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 479, 327–348.CrossRefGoogle Scholar
Marmottant, P. & Hilgenfeldt, S. 2004 A bubble-driven microfluidic transport element for bioengineering. Proc. Natl Acad. Sci. USA 101 (26), 9523–9527.Google Scholar
Obreschkow, D., Bruderer, M. & Farhat, M. 2012 Analytical approximations for the collapse of an empty spherical bubble. Phys. Rev. E 85, 066303.Google Scholar
Obreschkow, D., Tinguely, M., Dorsaz, N., Kobel, P., de Bosset, A. & Farhat, M. 2011 Universal scaling law for jets of collapsing bubbles. Phys. Rev. Lett. 107, 204501.Google Scholar
Obreschkow, D., Tinguely, M., Dorsaz, N., Kobel, P., de Bosset, A. & Farhat, M. 2013 The quest for the most spherical bubble: experimental setup and data overview. Exp. Fluids 54 (4), 1–18.CrossRefGoogle Scholar
Ohl, C. D. & Ikink, R. 2003 Shock-wave-induced jetting of micron-size bubbles. Phys. Rev. Lett. 90 (21), 214502.Google Scholar
Ohl, C.-D., Kurz, T., Geisler, R., Lindau, O. & Lauterborn, W. 1999 Bubble dynamics, shock waves and sonoluminescence. Phil. Trans. R. Soc. Lond. 357, 269–294.CrossRefGoogle Scholar
Ohl, C.-D., Lindau, O. & Lauterborn, W. 1998 Luminescence from spherically and aspherically collapsing laser induced bubbles. Phys. Rev. Lett. 80 (2), 393.Google Scholar
Philipp, A. & Lauterborn, W. 1998 Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 361, 75–116.Google Scholar
Plesset, M. S. & Chapman, R. B. 1970 Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary. J. Fluid Mech. 47, 283–290.Google Scholar
Rayleigh, Lord 1917 On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag. 34, 94–98.CrossRefGoogle Scholar
Robinson, P. B., Blake, J. R., Kodama, T., Shima, A. & Tomita, Y. 2001 Interaction of cavitation bubbles with a free surface. J. Appl. Phys. 89 (12), 8225–8237.Google Scholar
Sankin, G. N. 2005 Shock wave interaction with laser-generated single bubbles. Phys. Rev. Lett. 95, 034501.Google Scholar
Sankin, G. N., Yuan, F. & Zhong, P. 2010 Pulsating tandem microbubble for localized and directional single-cell membrane poration. Phys. Rev. Lett. 105, 078101.CrossRefGoogle ScholarPubMed
Silberrad, D. 1912 Propeller erosion. Engineering 33, 33–35.Google Scholar
Stride, E. & Edirisinghe, M. 2008 Novel microbubble preparation technologies. Soft Matt. 4, 2350–2359.Google Scholar
Supponen, O., Kobel, P., Obreschkow, D. & Farhat, M. 2015 The inner world of a collapsing bubble. Phys. Fluids 27, 091101.Google Scholar
Taib, B. B., Doherty, G. & Blake, J. R. 1983 High order boundary integral modelling of cavitation bubbles. In Proceedings of the 8th Australasian Fluid Mechanics Conference, University of Newcastle, 28 November–2 December 1983.Google Scholar
Tinguely, M.2013, The effect of pressure gradient on the collapse of cavitation bubbles in normal and reduced gravity. PhD thesis, Ecole Polytechnique Federale de Lausanne, Switzerland.Google Scholar
Tomita, Y. & Kodama, T. 2003 Interaction of laser-induced cavitation bubbles with composite surfaces. J. Appl. Phys. 94 (5), 2809–2816.CrossRefGoogle Scholar
Tomita, Y., Robinson, P. B., Tong, R. P. & Blake, J. R. 2002 Growth and collapse of cavitation bubbles near a curved rigid boundary. J. Fluid Mech. 466, 259–283.Google Scholar
Vogel, A., Lauterborn, W. & Timm, R. 1989 Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J. Fluid Mech. 206, 299–338.Google Scholar
Wang, Q. X., Yeo, K. S., Khoo, B. C. & Lam, K. Y. 2005 Vortex ring modelling of toroidal bubbles. Theor. Comput. Fluid Dyn. 19, 303–317.Google Scholar
Yin, Z. & Prosperetti, A. 2005 A microfluidic blinking bubble pump. J. Micromech. Microengng 15, 643–651.CrossRefGoogle Scholar
Zhang, A. M., Cui, P., Cui, J. & Wang, Q. X. 2015 Experimental study on bubble dynamics subject to buoyancy. J. Fluid Mech. 776, 137–160.CrossRefGoogle Scholar
Zhang, A. M., Cui, P. & Wang, Y. 2013 Experiments on bubble dynamics between a free surface and a rigid wall. Exp. Fluids 54 (10), 1–18.Google Scholar

Supponen et al. supplementary movie

Weak jet formation driven by gravity (see figure 4). The movie has been taken at 100 000 frames per second. The anisotropy parameter ζ equals 0.001.

Download Supponen et al. supplementary movie(Video)
Video 3.3 MB

Supponen et al. supplementary movie

Shock wave emission at the collapse of a bubble with a gravity-driven weak jet (see figure 5). The movie has been taken at 10 million frames per second. The anisotropy parameter ζ equals 0.001.

Download Supponen et al. supplementary movie(Video)
Video 8.7 MB

Supponen et al. supplementary movie

Bubble with an intermediate jet driven by gravity (see figure 6). The movie has been taken at 20 000 frames per second. The anisotropy parameter ζ equals 0.007.

Download Supponen et al. supplementary movie(Video)
Video 8.1 MB

Supponen et al. supplementary movie

Bubble with an intermediate jet driven by a nearby free surface (see figure 6). The movie has been taken at 20 000 frames per second. The anisotropy parameter ζ equals 0.007.

Download Supponen et al. supplementary movie(Video)
Video 9.2 MB

Supponen et al. supplementary movie

Shock wave emission at the collapse of a bubble with a gravity-driven intermediate jet (see figure 7). The movie has been taken at 10 million frames per second. The anisotropy parameter ζ equals 0.007.

Download Supponen et al. supplementary movie(Video)
Video 5.6 MB