Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T05:43:22.582Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling behaviour in Rayleigh–Bénard convection with and without rotation

Published online by Cambridge University Press:  01 February 2013

E. M. King ,
S. Stellmach  and
B. Buffett
E. M. King*
Affiliation:
Department of Earth and Planetary Science, University of California, Berkeley, CA 94720-4767, USA Department of Physics, University of California, Berkeley, CA 94720-7300, USA
S. Stellmach
Affiliation:
Institut für Geophysik, WWU Münster, Corrensstrasse 24, 48149 Münster, Germany
B. Buffett
Affiliation:
Department of Earth and Planetary Science, University of California, Berkeley, CA 94720-4767, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

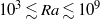Rotating Rayleigh–Bénard convection provides a simplified dynamical analogue for many planetary and stellar fluid systems. Here, we use numerical simulations of rotating Rayleigh–Bénard convection to investigate the scaling behaviour of five quantities over a range of Rayleigh ($1{0}^{3} \lesssim \mathit{Ra}\lesssim 1{0}^{9} $), Prandtl ($1\leq \mathit{Pr}\leq 100$) and Ekman ($1{0}^{- 6} \leq E\leq \infty $) numbers. The five quantities of interest are the viscous and thermal boundary layer thicknesses, 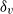${\delta }_{v} $ and 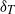${\delta }_{T} $, mean temperature gradients, 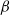$\beta $, characteristic horizontal length scales, 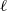$\ell $, and flow speeds, 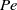$\mathit{Pe}$. Three parameter regimes in which different scalings apply are quantified: non-rotating, weakly rotating and rotationally constrained. In the rotationally constrained regime, all five quantities are affected by rotation. In the weakly rotating regime, 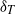${\delta }_{T} $, 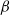$\beta $ and 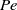$\mathit{Pe}$, roughly conform to their non-rotating behaviour, but 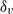${\delta }_{v} $ and 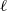$\ell $ are still strongly affected by the Coriolis force. A summary of scaling results is given in table 2.

JFM classification

Convection: Convection Geophysical and Geological Flows: Geophysical and Geological Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 449 - 471
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Aubert, J., Brito, D., Nataf, H. & Cardin, P. 2001 A systematic experimental study of rapidly rotating spherical convection in water and liquid gallium. Phys. Earth Planet. Inter. 128, 51–74.CrossRefGoogle Scholar
Barenblatt, G. I. 2003 Scaling. Cambridge University Press.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50 (1), 269–280.Google Scholar
Bénard, H. 1900 Étude expérimentale des courants de convection dans une nappe liquide – régime permanent: tourbillons cellulaires. J. Phys. Théor. Appl. 9, 513–524.Google Scholar
Boubnov, B. & Golitsyn, G. 1990 Temperature and velocity-field regimes of convective motions in a rotating plane fluid layer. J. Fluid Mech. 219, 215–239.CrossRefGoogle Scholar
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69 (2), 026302.CrossRefGoogle ScholarPubMed
Calzavarini, E., Lohse, D., Toschi, F. & Trippiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk of Rayleigh–Bénard turbulence. Phys. Fluids 17, 055107.Google Scholar
Chandrasekhar, S. 1953 The instability of a layer of fluid heated below and subject to Coriolis forces. Proc. R. Soc. Lond. A 217 (1130), 306–327.Google Scholar
Ekman, V. 1905 On the influence of the Earth’s rotation on ocean currents. Ark. Mat. Astron. Fys. 2, 1–53.Google Scholar
Fernando, H. J. S., Chen, R. R. & Boyer, D. L. 1991 Effects of rotation on convective turbulence. J. Fluid Mech. 228, 513–547.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92 (19), 194502.Google Scholar
Gillet, N. & Jones, C. 2006 The quasi-geostrophic model for rapidly rotating spherical convection outside the tangent cylinder. J. Fluid Mech. 554, 343–369.Google Scholar
Greenspan, H. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Julien, K., Knobloch, E. & Werne, J. 1998 A new class of equations for rotationally constrained flows. Theor. Comput. Fluid Dyn. 11, 251–261.Google Scholar
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.CrossRefGoogle Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012 Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 392–428.CrossRefGoogle Scholar
King, E. M. 2009 An investigation of planetary convection: the role of boundary layers. PhD thesis, University of California, Los Angeles.Google Scholar
King, E. M. & Aurnou, J. M. 2012 Thermal evidence for Taylor columns in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 85, 016313.Google Scholar
King, E., Soderlund, K., Christensen, U. R., Wicht, J. & Aurnou, J. M. 2010 Convective heat transfer in planetary dynamo models. Geochem. Geophys. Geosyst. 11 (6), Q06016.Google Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.Google Scholar
King, E., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. 2009 Boundary layer control of rotating convection systems. Nature 457 (7227), 301–304.Google Scholar
Kundu, P. K. 1990 Fluid Mechanics. Academic Press.Google Scholar
Kunnen, R., Clercx, H. & Geurts, B. 2006 Heat flux intensification by vortical flow localization in rotating convection. Phys. Rev. E 74 (5), 4.Google Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65 (6), 066306.Google Scholar
Liu, Y. M. & Ecke, R. E. 1997 Heat transport scaling in turbulent Rayleigh–Bénard convection: effects of rotation and Prandtl number. Phys. Rev. Lett. 79 (12), 2257–2260.Google Scholar
Liu, Y. & Ecke, R. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80 (3), 6314–6325.CrossRefGoogle ScholarPubMed
Niemela, J. J., Babuin, S. & Sreenivasan, K. R. 2010 Turbulent rotating convection at high Rayleigh and Taylor numbers. J. Fluid Mech. 649, 509.Google Scholar
Niemela, J. J. & Sreenivasan, K. R. 2006 Turbulent convection at high Rayleigh numbers and aspect ratio 4. J. Fluid Mech. 557, 411–422.Google Scholar
Olson, P. & Corcos, G. M. 1980 A boundary layer model for mantle convection with surface plates. Geophys. J. R. Astron. Soc. 62, 195–219.Google Scholar
Parmentier, E. M. & Sotin, C. 2000 Three-dimensional numerical experiments on thermal convection in a very viscous fluid: implications for the dynamics of a thermal boundary layer at high Rayleigh number. Phys. Fluids 12 (3), 609–617.Google Scholar
Proudman, J. 1916 On the motions of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 96 (642), 408–424.Google Scholar
Qiu, X. L. & Xia, K.-Q. 1998a Spatial structure of the viscous boundary layer in turbulent convection. Phys. Rev. E 58 (5), 5816.Google Scholar
Qiu, X. L. & Xia, K.-Q. 1998b Viscous boundary layers at the sidewall of a convection cell. Phys. Rev. E 58 (1), 486–491.Google Scholar
Rayleigh, Lord 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. Ser. 6 32 (192), 529–546.Google Scholar
Rossby, H. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36 (2), 309–335.Google Scholar
Schmitz, S. & Tilgner, A. 2009 Heat transport in rotating convection without Ekman layers. Phys. Rev. E 80 (1), 5305–5307.Google Scholar
Schmitz, S. & Tilgner, A. 2010 Transitions in turbulent rotating Rayleigh–Benard convection. Geophys. Astrophys. Fluid Dyn. 104, 481–489.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42 (6), 3650–3653.CrossRefGoogle ScholarPubMed
Silano, G., Sreenivasan, K. R. & Verzicco, R. 2010 Numerical simulations of Rayleigh–Bénard convection for Prandtl numbers between $1{0}^{1} $ and $1{0}^{4} $ and Rayleigh numbers between $1{0}^{5} $ and $1{0}^{9} $ . J. Fluid Mech. 662, 409–446.Google Scholar
Snedecor, G. W. & Cochran, W. G. 1980 Statistical Methods. Iowa State University Press.Google Scholar
Spiegel, E. 1971 Convection in stars. I. Basic Boussinesq convection. Annu. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.Google Scholar
Stellmach, S. & Hansen, U. 2008 An efficient spectral method for the simulation of dynamos in Cartesian geometry and its implementation on massively parallel computers. Geochem. Geophys. Geosyst. 9 (5).Google Scholar
Sun, C., Cheung, Y. H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Taylor, G. I. 1921 Experiments with rotating fluids. Proc. R. Soc. Lond. A 100 (703), 114–121.Google Scholar
Xi, H., Lam, S. & Xia, K. 2004 From laminar plumes to organized flows: the onset of large–scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.Google Scholar
Zhong, S. 2005 Dynamics of thermal plumes in three-dimensional isoviscous thermal convection. Geophys. J. Intl 162 (1), 289–300.Google Scholar
Zhong, J., Stevens, R. & Clercx, H. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.CrossRefGoogle ScholarPubMed