Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T12:21:23.221Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling behaviour in impulsively started viscous flow past a finite flat plate

Published online by Cambridge University Press:  04 September 2014

Ling Xu  and
Monika Nitsche
Ling Xu
Affiliation:
Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, IN 46556, USA
Monika Nitsche*
Affiliation:
Department of Mathematics and Statistics, University of New Mexico, Albuquerque, NM 87131, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Viscous flow past a finite flat plate which is impulsively started in the direction normal to itself is studied numerically using a high-order mixed finite-difference and semi-Lagrangian scheme. The goal is to resolve the details of the vorticity generation, and to determine the dependence of the flow on time and Reynolds number. Vorticity contours, streaklines and streamlines are presented for a range of times 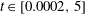$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}t\in [0.0002,5]$ and Reynolds numbers 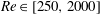$\mathit{Re}\in [250,2000]$, non-dimensionalized with respect to the driving velocity and the plate length. At early times, the starting vortex is small relative to the plate length and is expected to grow as if an external length scale were absent. We identify three different types of scaling behaviours consistent with this premise. (i) At early times, solutions with different values of $\mathit{Re}$ are identical up to rescaling. (ii) The solution for fixed $\mathit{Re}$ satisfies a viscous similarity law in time, locally in space, as illustrated by the core vorticity maximum, the upstream boundary layer thickness, and the maximum speed, in three different regions of the flow. (iii) The vortex core trajectory and the shed circulation satisfy inviscid scaling laws for several decades in time, and are consequently essentially 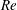$\mathit{Re}$-independent at these times. In addition, the computed induced drag and tangential forces are found to follow approximate scaling laws that define their dependence on time and 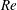$\mathit{Re}$.

JFM classification

Vortex Flows: Vortex Flows Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 689 - 715
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. & Shelley, M. J. 2008 Flapping states of a flag in an inviscid fluid: bistability and the transition to chaos. Phys. Rev. Lett. 100, 074301.CrossRefGoogle Scholar
Cortelezzi, L. & Leonard, A. 1993 Point vortex model of the unsteady separated flow past a semi-infinted plate with transverse motion. Fluid Dyn. Res. 11, 264–295.Google Scholar
Dennis, S. C. R., Qiang, W., Coutanceau, M. & Launay, J.-L. 1993 Viscous flow normal to a flat plate at moderate Reynolds numbers. J. Fluid Mech. 248, 605–635.Google Scholar
E, W. & Liu, J. G. 1996 Essentially compact schemes for unsteady viscous incompressible flows. J. Comput. Phys. 126, 122–138.Google Scholar
Eldredge, J. D. 2007 Numerical simulation of the fluid dynamics of 2D rigid body motion with the vortex particle method. J. Comput. Phys. 221, 626–648.Google Scholar
Fletcher, C. A. J. 1991 Computational Techniques for Fluid Dynamics, Vol. 1. Springer.Google Scholar
Hudson, J. D. & Dennis, S. C. R. 1985 The flow of a viscous incompressible fluid past a normal flat plate at low and intermediate Reynolds numbers: the wake. J. Fluid Mech. 160, 369–383.Google Scholar
Johnston, H. & Krasny, R. 2002 Fourth-order finite difference simulation of a differentially heated cavity. Intl J. Numer. Meth. Fluids 40, 1031–1037.Google Scholar
Jones, M. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.Google Scholar
Jones, M. A. & Shelley, M. J. 2005 Falling cards. J. Fluid Mech. 540, 393–425.Google Scholar
Kaden, H. 1931 Aufwicklung einer unstabilen Unstetigkeitsfläche. Ing.-Arch. 2, 140–179; (NASA Technical Translation: Curling of an unstable discontinuity surface, NASA-TT-F-14230, 51 p, 1971.) (English trans. R.A.Lib.Trans. no. 403).Google Scholar
Koumoutsakos, P. & Shiels, D. 1996 Simulation of the viscous flow normal to an impulsively started and uniformly accelerated flat plate. J. Fluid Mech. 328, 177–277.Google Scholar
Krasny, R. 1991 Vortex sheet computations: roll-up, wakes, separation. Lect. Appl. Maths 28, 385–402.Google Scholar
Lepage, C., Leweke, T. & Verga, A. 2005 Spiral shear layers: roll-up and incipient instability. Phys. Fluids 17, 031705.Google Scholar
Lian, Q. X. & Huang, Z. 1989 Starting flow and structure of the starting vortex behind bluff bodies with sharp edges. Exp. Fluids 8, 95–103.CrossRefGoogle Scholar
Luchini, P. & Tognaccini, R. 2002 The start-up vortex issuing from a semi-infinite flat plate. J. Fluid Mech. 455, 175–193.Google Scholar
Lugt, H. J. 1995 Vortex Flow in Nature and Technology. Krieger Publishing Company.Google Scholar
Michelin, S. & Llewellyn Smith, S. G. 2009 An unsteady point vortex method for coupled fluid–solid problems. Theor. Comput. Fluid Dyn. 23, 127–153.Google Scholar
Nitsche, M. & Krasny, R. 1994 A numerical study of vortex ring formation at the edge of a circular tube. J. Fluid Mech. 276, 139–161.Google Scholar
Nitsche, M., Taylor, M. A. & Krasny, R. 2003 Comparison of regularizations of vortex sheet motion. In Computational Fluid and Solid Mechanics (ed. Bathe, K. J.), Elsevier Science.Google Scholar
Nitsche, M. & Xu, L. 2014 Circulation shedding in viscous starting flow past a flat plate. Fluid Dyn. Res. 46 (6, Part 2).Google Scholar
Pierce, D. 1961 Photographic evidence of the formation and growth of vorticity behind plates accelerated from rest in still air. J. Fluid Mech. 11, 460–464.Google Scholar
Pullin, D. I. 1978 The large-scale structure of unsteady self-similar rolled-up vortex sheets. J. Fluid Mech. 88, 401–430.Google Scholar
Pullin, D. I. & Perry, A. E. 1980 Some flow visualization experiments on the starting vortex. J. Fluid Mech. 97, 239–255.Google Scholar
Schneider, K., Paget-Goy, M., Vega, A. & Farge, M. 2014 Numerical simulation of flows past flat plates using volume penalization. Comput. Appl. Math. 33 (2), 481–495.Google Scholar
Seaid, M. 2002 Semi-Lagrangian integration schemes for viscous incompressible flows. Comput. Meth. Appl. Maths 2, 392–409.Google Scholar
Sherman, F. S. 1990 Viscous Flow. McGraw-Hill.Google Scholar
Shukla, R. K. & Eldredge, J. D. 2007 An inviscid model for vortex shedding from a deforming body. Theor. Comput. Fluid Dyn. 21, 343–368.Google Scholar
Staniforth, A. & Côté, J. 1991 Semi-Lagrangian integration schemes for atmospheric models – a review. Mon. Weath. Rev. 119, 2206–2223.2.0.CO;2>CrossRefGoogle Scholar
Strikwerda, J. C. 1989 Finite Difference Schemes and Partial Differential Equations. Wadsworth and Brooks/Coles.Google Scholar
Taneda, S. & Honji, H. 1971 Unsteady flow past a flat plate normal to the direction of motion. J. Phys. Soc. Japan 30, 262–272.Google Scholar
Van Dyke, M. 1982 An Album of Fluid Motion. Parabolic Press.CrossRefGoogle Scholar
Wang, Z. J. 2000 Vortex shedding and frequency selection in flapping flight. J. Fluid Mech. 410, 323–341.CrossRefGoogle Scholar
Wang, C. & Eldredge, J. D. 2013 Low-order phenomenological modeling of leading-edge vortex formation. Theor. Comput. Fluid Dyn. 27 (5), 577–598.CrossRefGoogle Scholar
Xu, L.2012 Viscous flow past flat plates. PhD thesis, University of New Mexico.Google Scholar
Xu, L. & Nitsche, M.2014 Start-up vortex flow past an accelerated flat plate (submitted) arXiv:1404.4585 [physics.flu-dyn].Google Scholar
Ysasi, A., Kanso, E. & Newton, P. K. 2011 Wake structure of a deformable Joukowski airfoil. In Fluid Dynamics: From Theory to Experiment, vol. 240, pp. 1574–1582.Google Scholar