Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T21:25:56.295Z Has data issue: false hasContentIssue false
  • English
  • Français

Scale-to-scale anisotropy in homogeneous turbulence

Published online by Cambridge University Press:  22 August 2017

Douglas W. Carter Open the ORCID record for Douglas W. Carter [Opens in a new window]  and
Filippo Coletti
Douglas W. Carter
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55414, USA Saint Anthony Falls Laboratory, Minneapolis, MN 55414, USA
Filippo Coletti*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55414, USA Saint Anthony Falls Laboratory, Minneapolis, MN 55414, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We experimentally investigate scale-to-scale anisotropy from the integral to the dissipative scales in homogeneous turbulence. We employ an apparatus in which two facing arrays of randomly actuated air jets generate turbulence with negligible mean flow and shear, over a volume several times larger than the energy-containing eddy size. The Reynolds number based on the Taylor microscale is varied in the range 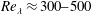$Re_{\unicode[STIX]{x1D706}}\approx 300{-}500$, while the axial-to-radial ratio of the root mean square velocity fluctuations ranges between 1.38 and 1.72. Two velocity components are measured by particle image velocimetry at varying resolutions, capturing from the integral to the Kolmogorov scales and yielding statistics up to sixth order. Over the inertial range, the scaling exponents of the velocity structure functions are found to differ not only between the longitudinal and transverse components, but also between the axial and radial directions of separation. At the dissipative scales, the moments of the velocity gradients indicate that departure from isotropy is, at the present Reynolds numbers, significant and more pronounced for stronger large-scale anisotropy. The generalized flatness factors of the longitudinal velocity differences tend towards isotropy as the separation is reduced from the inertial to the near-dissipative scales (down to about 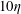$10\unicode[STIX]{x1D702}$, 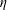$\unicode[STIX]{x1D702}$ being the Kolmogorov length), but become more anisotropic for even smaller scales which are characterized by high intermittency. At the large scales, the direction of turbulence forcing is associated with a larger integral length, defined as the distance over which the velocity component in a given direction is spatially correlated. Because of anisotropy, the definition of the integral length is not trivial and may lead to dissimilar conclusions on the qualitative behaviour of the large scales and on the quantitative values of the normalized dissipation. Alternative definitions of these quantities are proposed to account for the anisotropy. Overall, these results highlight the importance of evaluating both the different velocity components and the different spatial directions across all scales of the flow.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Intermittency Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 827 , 25 September 2017 , pp. 250 - 284
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Anselmet, F., Gagne, Y., Hopfinger, E. J. & Antonia, R. A. 1984 High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 140, 63–89.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L., Danaila, L. & Tang, S. L. 2017 Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 29 (2), 020715.CrossRefGoogle Scholar
Antonia, R. A., Kim, J. & Browne, L. W. B. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 2002 Small-scale turbulence characteristics of two-dimensional bluff body wakes. J. Fluid Mech. 459, 67–92.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Zhu, Y. 1998 Three-component vorticity measurements in a turbulent grid flow. J. Fluid Mech. 374, 29–57.CrossRefGoogle Scholar
Arad, I., Dhruva, B., Kurien, S., L’vov, V. S., Procaccia, I. & Sreenivasan, K. R. 1998 Extraction of anisotropic contributions in turbulent flows. Phys. Rev. Lett. 81 (24), 5330–5333.CrossRefGoogle Scholar
Arnéodo, A., Baudet, C., Belin, F., Benzi, R., Castaing, B., Chabaud, B., Chavarria, R., Ciliberto, S., Camussi, R., Chilla, F. et al. 1996 Structure functions in turbulence, in various flow configurations, at Reynolds number between 30 and 5000, using extended self-similarity. Europhys. Lett. 34 (6), 411.CrossRefGoogle Scholar
Belin, F., Maurer, J., Tabeling, P. & Willaime, H. 1997 Velocity gradient distributions in fully developed turbulence: an experimental study. Phys. Fluids 9 (12), 3843–3850.CrossRefGoogle Scholar
Bellani, G. & Variano, E. A. 2014 Homogeneity and isotropy in a laboratory turbulent flow. Exp. Fluids 55 (1), 1646.CrossRefGoogle Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48 (1), R29–R32.Google ScholarPubMed
Bewley, G. P., Chang, K., Bodenschatz, E.& International Collaboration for Turbulence 2012 On integral length scales in anisotropic turbulence. Phys. Fluids 24 (6), 061702.CrossRefGoogle Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414 (2–3), 43–164.CrossRefGoogle Scholar
Biferale, L. & Toschi, F. 2001 Anisotropic homogeneous turbulence: hierarchy and intermittency of scaling exponents in the anisotropic sectors. Phys. Rev. Lett. 86 (21), 4831–4834.CrossRefGoogle ScholarPubMed
Bos, W. J. T., Liechtenstein, L. & Schneider, K. 2007 Small-scale intermittency in anisotropic turbulence. Phys. Rev. E 76 (4), 046310.CrossRefGoogle ScholarPubMed
Briscolini, M., Santangelo, P., Succi, S. & Benzi, R. 1994 Extended self-similarity in the numerical simulation of three-dimensional homogeneous flows. Phys. Rev. E 50 (3), R1745.Google ScholarPubMed
Browne, L. W. B., Antonia, R. a. & Shah, D. a. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307.CrossRefGoogle Scholar
Burattini, P., Falchi, M., Romano, G. P. & Antonia, R. A. 2010 PIV and hot wire measurements in the far field of turbulent round jets. Meas. Sci. Technol. 21 (12), 125402.CrossRefGoogle Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17 (9), 098103.CrossRefGoogle Scholar
Cardesa, J. I., Nickels, T. B. & Dawson, J. R. 2012 2D PIV measurements in the near field of grid turbulence using stitched fields from multiple cameras. Exp. Fluids 52 (6), 1611–1627.CrossRefGoogle Scholar
Carter, D., Petersen, A., Amili, O. & Coletti, F. 2016 Generating and controlling homogeneous air turbulence using random jet arrays. Exp. Fluids 57 (12), 189.CrossRefGoogle Scholar
Casciola, C. M., Gualtieri, P., Jacob, B. & Piva, R. 2005 Scaling properties in the production range of shear dominated flows. Phys. Rev. Lett. 95 (2), 024503.CrossRefGoogle ScholarPubMed
Castaing, B., Gagne, Y. & Hopfinger, E. J. 1990 Velocity probability density functions of high Reynolds number turbulence. Physica D 46 (2), 177–200.CrossRefGoogle Scholar
Chang, K., Bewley, G. P. & Bodenschatz, E. 2012 Experimental study of the influence of anisotropy on the inertial scales of turbulence. J. Fluid Mech. 692, 464–481.CrossRefGoogle Scholar
Chen, S., Sreenivasan, K. R., Nelkin, M. & Cao, N. 1997 A refined similarity hypothesis for transverse structure functions. Phys. Rev. Lett. 79 (12), 4, arXiv:9704009.CrossRefGoogle Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97 (17), 174501.CrossRefGoogle ScholarPubMed
Chevillard, L., Roux, S. G., Lévêque, E., Mordant, N., Pinton, J.-F. & Arnéodo, A. 2005 Intermittency of velocity time increments in turbulence. Phys. Rev. Lett. 95 (6), 064501.CrossRefGoogle ScholarPubMed
Chien, C.-C., Blum, D. B. & Voth, G. A. 2013 Effects of fluctuating energy input on the small scales in turbulence. J. Fluid Mech. 737, 527–551.CrossRefGoogle Scholar
Christensen, K. T. 2004 The influence of peak-locking errors on turbulence statistics computed from PIV ensembles. Exp. Fluids 36 (3), 484–497.CrossRefGoogle Scholar
Davidson, P. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5.CrossRefGoogle Scholar
Dhruva, B., Tsuji, Y. & Sreenivasan, K. 1997 Transverse structure functions in high-Reynolds-number turbulence. Phys. Rev. E 56 (5), R4928–R4930.Google Scholar
Discetti, S., Ziskin, I. B., Astarita, T., Adrian, R. J. & Prestridge, K. P. 2013 PIV measurements of anisotropy and inhomogeneity in decaying fractal generated turbulence. Fluid Dyn. Res. 45 (6), 061401.CrossRefGoogle Scholar
Dou, Z., Pecenak, Z. K., Cao, L., Woodward, S. H., Liang, Z. & Meng, H. 2016 PIV measurement of high-Reynolds-number homogeneous and isotropic turbulence in an enclosed flow apparatus with fan agitation. Meas. Sci. Technol. 27 (3), 035305.CrossRefGoogle Scholar
Durbin, P. A. & Speziale, C. G. 1991 Local anisotropy in strained turbulence at high Reynolds numbers. Trans. ASME J. Fluids Engng 113 (4), 707.CrossRefGoogle Scholar
Elsinga, G. E. & Marusic, I. 2016 The anisotropic structure of turbulence and its energy spectrum. Phys. Fluids 28 (1), 011701.CrossRefGoogle Scholar
Fiscaletti, D., Ganapathisubramani, B. & Elsinga, G. E. 2017 Amplitude and frequency modulation of the small scales in a jet. J. Fluid Mech. 772, 756–783.CrossRefGoogle Scholar
Fiscaletti, D., Westerweel, J. & Elsinga, G. E. 2014 Long-range 𝜇PIV to resolve the small scales in a jet at high Reynolds number. Exp. Fluids 55 (9), 1812.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Fulachier, L. & Antonia, R. A. 1983 Turbulent Reynolds and Péclet numbers re-defined. Intl Commun. Heat Mass Transfer 10 (5), 435–439.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.CrossRefGoogle Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2007 Determination of complete velocity gradient tensor by using cinematographic stereoscopic PIV in a turbulent jet. Exp. Fluids 42 (6), 923–939.CrossRefGoogle Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.CrossRefGoogle Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 4 (7), 1492–1509.CrossRefGoogle Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2012 Particle image velocimetry study of fractral-generated turbulence. J. Fluid Mech. 711, 306–336.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2015 The energy cascade in near-field non-homogeneous non-isotropic turbulence. J. Fluid Mech. 771, 676–705.CrossRefGoogle Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14 (3), 1065–1081.CrossRefGoogle Scholar
Gylfason, A., Ayyalasomayajula, S. & Warhaft, Z. 2004 Intermittency, pressure and acceleration statistics from hot-wire measurements in wind-tunnel turbulence. J. Fluid Mech. 501, 213–229.CrossRefGoogle Scholar
He, G., Jin, G. & Yang, Y. 2017 Space–time correlations and dynamic coupling in turbulent flows. Annu. Rev. Fluid Mech. 49, 51–70.CrossRefGoogle Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.CrossRefGoogle Scholar
Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19 (3), 035103.CrossRefGoogle Scholar
Hussein, H. J. 1994 Evidence of local axisymmetry in the small scales of a turbulent planar jet. Phys. Fluids 6 (6), 2058.CrossRefGoogle Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41 (1), 165–180.CrossRefGoogle Scholar
Jacobitz, F. G., Schneider, K., Bos, W. J. T. & Farge, M. 2010 On the structure and dynamics of sheared and rotating turbulence: anisotropy properties and geometrical scale-dependent statistics. Phys. Fluids 22 (8), 085101.CrossRefGoogle Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
de Jong, J., Cao, L., Woodward, S. H., Salazar, J. P. L. C., Collins, L. R. & Meng, H. 2009 Dissipation rate estimation from PIV in zero-mean isotropic turbulence. Exp. Fluids 46 (3), 499–515.CrossRefGoogle Scholar
Kaneda, Y., Ishihara, T., Yokokawa, M., Itakura, K. & Uno, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box. Phys. Fluids 15 (2), L21–L24.CrossRefGoogle Scholar
Khorsandi, B., Gaskin, S. & Mydlarski, L. 2013 Effect of background turbulence on an axisymmetric turbulent jet. J. Fluid Mech. 736, 250–286.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (01), 82–85.CrossRefGoogle Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.CrossRefGoogle Scholar
Kurien, S. & Sreenivasan, K. R. 2000 Anisotropic scaling contributions to high-order structure functions in high-Reynolds-number turbulence. Phys. Rev. E 62 (2), 2206–2212.Google ScholarPubMed
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.CrossRefGoogle Scholar
Lawson, J. M. & Dawson, J. R. 2014 A scanning PIV method for fine-scale turbulence measurements. Exp. Fluids 55 (12), 1857.CrossRefGoogle Scholar
Lin, C. C. 1953 On Taylor’s hypothesis and the acceleration terms in the Navier–Stokes equation. Q. Appl. Maths 10 (4), 295–306.CrossRefGoogle Scholar
Maxey, M. R. 1987 The velocity skewness measured in grid turbulence. Phys. Fluids 30 (4), 935–938.CrossRefGoogle Scholar
Mazellier, N. & Vassilicos, J. C. 2008 The turbulence dissipation constant is not universal because of its universal dependence on large-scale flow topology. Phys. Fluids 20 (1), 015101.CrossRefGoogle Scholar
Meneveau, C. 1991 Dual spectra and mixed energy cascade of turbulence in the wavelet representation. Phys. Rev. Lett. 66 (11), 1450–1453.CrossRefGoogle ScholarPubMed
Mi, J. & Antonia, R. A. 2010 Approach to local axisymmetry in a turbulent cylinder wake. Exp. Fluids 48 (6), 933–947.CrossRefGoogle Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2006 Large-scale flow effects, energy transfer, and self-similarity on turbulence. Phys. Rev. E 74 (1), 016303.Google ScholarPubMed
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2, p. 874. MIT Press.Google Scholar
Mullin, J. A. & Dahm, W. J. A. 2006 Dual-plane stereo particle image velocimetry measurements of velocity gradient tensor fields in turbulent shear flow. II. Experimental results. Phys. Fluids 18 (3), 035102.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331.CrossRefGoogle Scholar
Noullez, A., Wallace, G., Lempert, W., Miles, R. B. & Frisch, U. 1997 Transverse velocity increments in turbulent flow using the RELIEF technique. J. Fluid Mech. 339, 287–307.CrossRefGoogle Scholar
Ouellette, N. T., Xu, H., Bourgoin, M. & Bodenschatz, E. 2006 Small-scale anisotropy in Lagrangian turbulence. New J. Phys. 8 (6), 102.CrossRefGoogle Scholar
Pérez-Alvarado, A., Mydlarski, L. & Gaskin, S. 2016 Effect of the driving algorithm on the turbulence generated by a random jet array. Exp. Fluids 57 (2), 20.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Rabey, P. K., Wynn, A. & Buxton, O. R. H. 2015 The kinematics of the reduced velocity gradient tensor in a fully developed turbulent free shear flow. J. Fluid Mech. 767, 627–658.CrossRefGoogle Scholar
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide. Springer Science & Business Media.CrossRefGoogle Scholar
Romano, G. P. & Antonia, R. A. 2001 Longitudinal and transverse structure functions in a turbulent round jet: effect of initial conditions and Reynolds number. J. Fluid Mech. 436, 231–248.CrossRefGoogle Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Shafi, H. S. & Antonia, R. a. 1997 Small-scale characteristics of a turbulent boundary layer over a rough wall. J. Fluid Mech. 342, 263–293.CrossRefGoogle Scholar
She, Z.-S. & Leveque, E. 1994 Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72 (3), 336–339.CrossRefGoogle ScholarPubMed
Shen, X. & Warhaft, Z. 2002 Longitudinal and transverse structure functions in sheared and unsheared wind-tunnel turbulence. Phys. Fluids 14 (1), 370–381.CrossRefGoogle Scholar
Siebert, H., Shaw, R. A. & Warhaft, Z. 2010 Statistics of small-scale velocity fluctuations and internal intermittency in marine stratocumulus clouds. J. Atmos. Sci. 67 (1), 262–273.CrossRefGoogle Scholar
Squire, D. T., Hutchins, N., Morrill-Winter, C., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2017 Applicability of Taylor’s hypothesis in rough- and smooth-wall boundary layers. J. Fluid Mech. 812, 398–417.CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (11), 2778–2784.CrossRefGoogle Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10 (2), 528–529.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phemonology of small scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.CrossRefGoogle Scholar
Sreenivasan, K. R. & Kailasnath, P. 1993 An update on the intermittency exponent in turbulence. Phys. Fluids A 5 (2), 512–514.CrossRefGoogle Scholar
Sreenivasan, K. R., Vainshtein, S. I., Bhiladvala, R., San Gil, I., Chen, S. & Cao, N. 1996 Asymmetry of velocity increments in fully developed turbulence and the scaling of low-order moments. Phys. Rev. Lett. 77 (8), 1488–1491.CrossRefGoogle ScholarPubMed
Staicu, A., Vorselaars, B. & van de Water, W. 2003 Turbulence anisotropy and the SO(3) description. Phys. Rev. E 68 (4), 046303.Google ScholarPubMed
Tabeling, P., Zocchi, G., Belin, F., Maurer, J. & Willaime, H. 1996 Probability density functions, skewness, and flatness in large Reynolds number turbulence. Phys. Rev. E 53 (2), 1613–1621.Google ScholarPubMed
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Thiesset, F., Danaila, L. & Antonia, R. A. 2013 Dynamical effect of the total strain induced by the coherent motion on local isotropy in a wake. J. Fluid Mech. 720, 393–423.CrossRefGoogle Scholar
Thormann, A. & Meneveau, C. 2014 Decay of homogeneous, nearly isotropic turbulence behind active fractal grids. Phys. Fluids 26 (2), 025112.CrossRefGoogle Scholar
Tritton, D. J. 1992 Stabilization and destabilization of turbulent shear flow in a rotating fluid. J. Fluid Mech. 241, 503–523.CrossRefGoogle Scholar
Tsinober, a., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity gradients in turbulent flows. J. Fluid Mech. 242, 169.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Dependence of decaying homogeneous isotropic turbulence on inflow conditions. Phys. Lett. A 376 (4), 510–514.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2014 The non-equilibrium region of grid-generated decaying turbulence. J. Fluid Mech. 744, 5–37.CrossRefGoogle Scholar
Variano, E. A. & Cowen, E. A. 2008 A random-jet-stirred turbulence tank. J. Fluid Mech. 604, 1–32.CrossRefGoogle Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47 (1), 95–114.CrossRefGoogle Scholar
Veeravalli, S. & Warhaft, Z. 1989 The shearless turbulence mixing layer. J. Fluid Mech. 207, 191.CrossRefGoogle Scholar
Voth, G. A., la Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.CrossRefGoogle Scholar
Wang, L.-P., Chen, S., Brasseur, J. G. & Wyngaard, J. C. 1996 Examination of hypotheses in the Kolmogorov refined turbulence theory through high-resolution simulations. Part 1. Velocity field. J. Fluid Mech. 309, 113–156.CrossRefGoogle Scholar
Warhaft, Z. 2009 Why we need experiments at high Reynolds numbers. Fluid Dyn. Res. 41 (2), 021401.CrossRefGoogle Scholar
Worth, N. A., Nickels, T. B. & Swaminathan, N. 2010 A tomographic PIV resolution study based on homogeneous isotropic turbulence DNS data. Exp. Fluids 49 (3), 637–656.CrossRefGoogle Scholar
Yeung, P. K. & Brasseur, J. G. 1991 The response of isotropic turbulence to isotropic and anisotropic forcing at the large scales. Phys. Fluids A 3 (5), 884–897.CrossRefGoogle Scholar
Zaman, K. B. M. Q. & Hussain, a. K. M. F. 1981 Taylor hypothesis and large-scale coherent structures. J. Fluid Mech. 112, 379–396.CrossRefGoogle Scholar
Zhou, T., Antonia, R. A., Danaila, L. & Anselmet, F. 2000 Transport equations for the mean energy and temperature dissipation rates in grid turbulence. Exp. Fluids 28 (2), 143–151.CrossRefGoogle Scholar
Zhou, T., Pearson, B. R. & Antonia, R. A. 2001 Comparison between temporal and spatial transverse velocity increments in a turbulent plane jet. Fluid Dyn. Res. 28 (2), 127–138.CrossRefGoogle Scholar