Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-25T12:57:56.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Scales and self-sustained mechanism of reattachment unsteadiness in separated shock wave/boundary layer interaction

Published online by Cambridge University Press:  04 November 2024

Wen-Feng Zhou Open the ORCID record for Wen-Feng Zhou [Opens in a new window] ,
Yan-Chao Hu Open the ORCID record for Yan-Chao Hu [Opens in a new window] ,
Ming-Zhi Tang ,
Gang Wang ,
Yan-Guang Yang  and
Zhi-Gong Tang
Wen-Feng Zhou
Affiliation:
Hypervelocity Aerodynamics Institute (HAI), China Aerodynamics Research and Development Center, Mianyang 621000, PR China National Key Laboratory of Aerospace Physics in Fluids, Mianyang 621000, PR China
Yan-Chao Hu*
Affiliation:
Hypervelocity Aerodynamics Institute (HAI), China Aerodynamics Research and Development Center, Mianyang 621000, PR China National Key Laboratory of Aerospace Physics in Fluids, Mianyang 621000, PR China
Ming-Zhi Tang
Affiliation:
Hypervelocity Aerodynamics Institute (HAI), China Aerodynamics Research and Development Center, Mianyang 621000, PR China National Key Laboratory of Aerospace Physics in Fluids, Mianyang 621000, PR China
Gang Wang
Affiliation:
Hypervelocity Aerodynamics Institute (HAI), China Aerodynamics Research and Development Center, Mianyang 621000, PR China National Key Laboratory of Aerospace Physics in Fluids, Mianyang 621000, PR China
Yan-Guang Yang*
Affiliation:
National Key Laboratory of Aerospace Physics in Fluids, Mianyang 621000, PR China China Aerodynamics Research and Development Center, Mianyang 621000, PR China
Zhi-Gong Tang
Affiliation:
China Aerodynamics Research and Development Center, Mianyang 621000, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

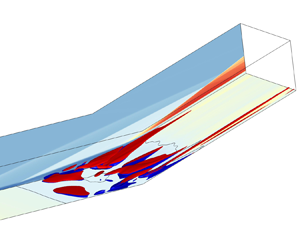
The spatio-temporal scales, as well as a comprehensive self-sustained mechanism of the reattachment unsteadiness in shock wave/boundary layer interaction, are investigated in this study. Direct numerical simulations reveal that the reattachment unsteadiness of a Mach 7.7 laminar inflow causes over $26\,\%$ variation in wall friction and up to $20\,\%$ fluctuation in heat flux at the reattachment of the separation bubble. A statistical approach, based on the local reattachment upstream movement, is proposed to identify the spanwise and temporal scales of reattachment unsteadiness. It is found that two different types, i.e. self-induced and random processes, dominate different regions of reattachment. A self-sustained mechanism is proposed to comprehend the reattachment unsteadiness in the self-induced region. The intrinsic instability of the separation bubble transports vorticity downstream, resulting in an inhomogeneous reattachment line, which gives rise to baroclinic production of quasi-streamwise vortices. The pairing of these vortices initiates high-speed streaks and shifts the reattachment line upstream. Ultimately, viscosity dissipates the vortices, triggering instability and a new cycle of reattachment unsteadiness. The temporal scale and maximum vorticity are estimated with the self-sustained mechanism via order-of-magnitude analysis of the enstrophy. The advection speed of friction, derived from the assumption of coherent structures advecting with a Blasius-type boundary layer, aligns with the numerical findings.

JFM classification

Aerodynamics: High-speed flow Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 998 , 10 November 2024 , A54
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adrian, R.J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
Anderson, J.D. 2019 Hypersonic and High-Temperature Gas Dynamics, 3rd edn. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Babinsky, H. & Harvey, J.K. (Eds) 2011 Shock Wave–Boundary-Layer Interactions, 1st edn. Cambridge University Press.CrossRefGoogle Scholar
Balantrapu, N.A., Alexander, W.N. & Devenport, W. 2023 Wall-pressure fluctuations in an axisymmetric boundary layer under strong adverse pressure gradient. J. Fluid Mech. 960, A28.CrossRefGoogle Scholar
Bugeat, B., Robinet, J.-C., Chassaing, J.-C. & Sagaut, P. 2022 Low-frequency resolvent analysis of the laminar oblique shock wave/boundary layer interaction. J. Fluid Mech. 942, A43.CrossRefGoogle Scholar
Cao, S., Hao, J., Klioutchnikov, I., Olivier, H. & Wen, C.-Y. 2021 a Unsteady effects in a hypersonic compression ramp flow with laminar separation. J. Fluid Mech. 912, A3.CrossRefGoogle Scholar
Cao, S., Hao, J., Klioutchnikov, I., Wen, C.-Y., Olivier, H. & Heufer, K.A. 2022 Transition to turbulence in hypersonic flow over a compression ramp due to intrinsic instability. J. Fluid Mech. 941, A8.CrossRefGoogle Scholar
Cao, S., Klioutchnikov, I. & Olivier, H. 2019 Görtler vortices in hypersonic flow on compression ramps. AIAA J. 57 (9), 3874–3884.CrossRefGoogle Scholar
Cao, S., Olivier, H. & Schröder, W. 2021 b Streamwise vortices in hypersonic flow on a compression ramp. Tech. Rep. Lehr-und Forschungsgebiet und Abteilung Hochtemperatur-Gasdynamik.Google Scholar
Ceci, A., Palumbo, A., Larsson, J. & Pirozzoli, S. 2023 On low-frequency unsteadiness in swept shock wave–boundary layer interactions. J. Fluid Mech. 956, R1.CrossRefGoogle Scholar
Chang, E.W.K., Chan, W.Y.K., McIntyre, T.J. & Veeraragavan, A. 2022 Hypersonic shock impingement studies on a flat plate: flow separation of laminar boundary layers. J. Fluid Mech. 951, A19.CrossRefGoogle Scholar
Chen, X., Huang, G.L. & Lee, C.B. 2019 Hypersonic boundary layer transition on a concave wall: stationary Görtler vortices. J. Fluid Mech. 865, 1–40.CrossRefGoogle Scholar
de la Chevalerie, D.A., Fonteneau, A., De Luca, L. & Cardone, G. 1997 Görtler-type vortices in hypersonic flows: the ramp problem. Expl Therm. Fluid Sci. 15 (2), 69–81.CrossRefGoogle Scholar
Chuvakhov, P.V., Borovoy, V.Y., Egorov, I.V., Radchenko, V.N., Olivier, H. & Roghelia, A. 2017 Effect of small bluntness on formation of Görtler vortices in a supersonic compression corner flow. J. Appl. Mech. Tech. Phys. 58 (6), 975–989.CrossRefGoogle Scholar
Clemens, N.T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46 (1), 469–492.CrossRefGoogle Scholar
Deshpande, A.S. & Poggie, J. 2020 Unsteady characteristics of compressible reattaching shear layers. Phys. Fluids 32 (6), 066103.CrossRefGoogle Scholar
Dolling, D.S. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
Dwivedi, A., Sidharth, G.S., Nichols, J.W., Candler, G.V. & Jovanović, M.R. 2019 Reattachment streaks in hypersonic compression ramp flow: an input–output analysis. J. Fluid Mech. 880, 113–135.CrossRefGoogle Scholar
Gaitonde, D.V. & Adler, M.C. 2023 Dynamics of three-dimensional shock-wave/boundary-layer interactions. Annu. Rev. Fluid Mech. 55 (1), 291–321.CrossRefGoogle Scholar
Ganapathisubramani, B., Clemens, N.T. & Dolling, D.S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.CrossRefGoogle Scholar
Ginoux, J.J. 1971 Streamwise vortices in reattaching high-speed flows – a suggested approach. AIAA J. 9 (4), 759–760.CrossRefGoogle Scholar
Gottlieb, S. & Shu, C.-W. 1998 Total variation diminishing Runge–Kutta schemes. Maths Comput. 67 (221), 73–85.CrossRefGoogle Scholar
Graham, M.D. & Floryan, D. 2021 Exact coherent states and the nonlinear dynamics of wall-bounded turbulent flows. Annu. Rev. Fluid Mech. 53 (1), 227–253.CrossRefGoogle Scholar
Gs, S., Dwivedi, A., Candler, G.V. & Nichols, J.W. 2018 Onset of three-dimensionality in supersonic flow over a slender double wedge. Phys. Rev. Fluids 3 (9), 093901.CrossRefGoogle Scholar
Guiho, F., Alizard, F. & Robinet, J.-C. 2016 Instabilities in oblique shock wave/laminar boundary-layer interactions. J. Fluid Mech. 789, 1–35.CrossRefGoogle Scholar
Hamilton, J.M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hao, J. 2023 On the low-frequency unsteadiness in shock wave–turbulent boundary layer interactions. J. Fluid Mech. 971, A28.CrossRefGoogle Scholar
Hao, J., Cao, S., Wen, C.-Y. & Olivier, H. 2021 Occurrence of global instability in hypersonic compression corner flow. J. Fluid Mech. 919, A4.CrossRefGoogle Scholar
Hao, J., Fan, J., Cao, S. & Wen, C.-Y. 2022 Three-dimensionality of hypersonic laminar flow over a double cone. J. Fluid Mech. 935, A8.CrossRefGoogle Scholar
Hildebrand, N., Dwivedi, A., Nichols, J.W., Jovanović, M.R. & Candler, G.V. 2018 Simulation and stability analysis of oblique shock-wave/boundary-layer interactions at Mach 5.92. Phys. Rev. Fluids 3 (1), 013906.CrossRefGoogle Scholar
Hof, B., van Doorne, C.W.H., Westerweel, J., Nieuwstadt, F.T.M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R.R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.CrossRefGoogle ScholarPubMed
Hu, W., Hickel, S. & van Oudheusden, B.W. 2021 Low-frequency unsteadiness mechanisms in shock wave/turbulent boundary layer interactions over a backward-facing step. J. Fluid Mech. 915, A107.CrossRefGoogle Scholar
Hu, Y.C., Bi, W.T., Li, S.Y. & She, Z.S. 2017 $\beta$-distribution for Reynolds stress and turbulent heat flux in relaxation turbulent boundary layer of compression ramp. Sci. China Phys. Mech. Astron. 60 (12), 124711.CrossRefGoogle Scholar
Hu, Y.-C., Zhou, W.-F., Tang, M.-Z., Wang, G., Yang, Y.-G. & Tang, Z.-G. 2024 DNS study of the bistable states in curved compression ramp flows. Phys. Rev. Fluids (submitted). arXiv:2304.03429.Google Scholar
Hu, Y.-C., Zhou, W.-F., Wang, G., Yang, Y.-G. & Tang, Z.-G. 2020 a Bistable states and separation hysteresis in curved compression ramp flows. Phys. Fluids 32 (11), 113601.CrossRefGoogle Scholar
Hu, Y.-C., Zhou, W.-F., Yang, Y.-G. & Tang, Z.-G. 2020 b Prediction of plateau and peak of pressure in a compression ramp flow with large separation. Phys. Fluids 32 (10), 101702.CrossRefGoogle Scholar
Huang, X. & Estruch-Samper, D. 2018 Low-frequency unsteadiness of swept shock-wave/turbulent- boundary-layer interaction. J. Fluid Mech. 856, 797–821.CrossRefGoogle Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jovanović, M.R., Schmid, P.J. & Nichols, J.W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26 (2), 024103.CrossRefGoogle Scholar
Kavun, I.N., Lipatov, I.I. & Zapryagaev, V.I. 2019 Flow effects in the reattachment region of supersonic laminar separated flow. Intl J. Heat Mass Transfer 129, 997–1009.CrossRefGoogle Scholar
Kline, S.J., Reynolds, W.C., Schraub, F.A. & Runstadler, P.W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.CrossRefGoogle Scholar
Knight, D., Yan, H., Panaras, A.G. & Zheltovodov, A. 2003 Advances in CFD prediction of shock wave turbulent boundary layer interactions. Prog. Aerosp. Sci. 39 (2–3), 121–184.CrossRefGoogle Scholar
Kutz, J.N., Brunton, S.L., Brunton, B.W. & Proctor, J.L. 2016 Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Li, X.L., Fu, D.X. & Ma, Y.W. 2008 DNS of compressible turbulent boundary layer around a sharp cone. Sci. China G 51 (6), 699–714.CrossRefGoogle Scholar
Li, X.L., Fu, D.X., Ma, Y.W. & Liang, X. 2010 Direct numerical simulation of shock/turbulent boundary layer interaction in a supersonic compression ramp. Sci. China Phys. Mech. Astron. 53 (9), 1651–1658.CrossRefGoogle Scholar
Lighthill, M.J. 1953 On boundary layers and upstream influence. II. Supersonic flows without separation. Proc. R. Soc. Lond. A 217 (1131), 478–507.Google Scholar
Lugrin, M., Beneddine, S., Leclercq, C., Garnier, E. & Bur, R. 2021 Transition scenario in hypersonic axisymmetrical compression ramp flow. J. Fluid Mech. 907, A6.CrossRefGoogle Scholar
Martín, M.P., Taylor, E.M., Wu, M. & Weirs, V.G. 2006 A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence. J. Comput. Phys. 220 (1), 270–289.CrossRefGoogle Scholar
Navarro-Martinez, S. & Tutty, O.R. 2005 Numerical simulation of Görtler vortices in hypersonic compression ramps. Comput. Fluids 34 (2), 225–247.CrossRefGoogle Scholar
Nichols, J.W., Larsson, J., Bernardini, M. & Pirozzoli, S. 2017 Stability and modal analysis of shock/boundary layer interactions. Theor. Comput. Fluid Dyn. 31 (1), 33–50.CrossRefGoogle Scholar
Pasquariello, V., Hickel, S. & Adams, N.A. 2017 Unsteady effects of strong shock-wave/boundary-layer interaction at high Reynolds number. J. Fluid Mech. 823, 617–657.CrossRefGoogle Scholar
Priebe, S. & Martín, M.P. 2012 Low-frequency unsteadiness in shock wave–turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.CrossRefGoogle Scholar
Priebe, S., Tu, J.H., Rowley, C.W. & Martín, M.P. 2016 Low-frequency dynamics in a shock-induced separated flow. J. Fluid Mech. 807, 441–477.CrossRefGoogle Scholar
Ren, J. & Fu, S. 2015 Secondary instabilities of Görtler vortices in high-speed boundary layer flows. J. Fluid Mech. 781, 388–421.CrossRefGoogle Scholar
Robinet, J.-C. 2007 Bifurcations in shock-wave/laminar-boundary-layer interaction: global instability approach. J. Fluid Mech. 579, 85–112.CrossRefGoogle Scholar
Robinson, S.K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.CrossRefGoogle Scholar
Rodriguez, D., Gennaro, E.M. & Souza, L.F. 2021 Self-excited primary and secondary instability of laminar separation bubbles. J. Fluid Mech. 906, A13.CrossRefGoogle Scholar
Roghelia, A., Olivier, H., Egorov, I. & Chuvakhov, P. 2017 Experimental investigation of Görtler vortices in hypersonic ramp flows. Exp. Fluids 58 (10), 139.CrossRefGoogle Scholar
Sansica, A., Sandham, N.D. & Hu, Z. 2016 Instability and low-frequency unsteadiness in a shock-induced laminar separation bubble. J. Fluid Mech. 798, 5–26.CrossRefGoogle Scholar
Sawant, S.S., Theofilis, V. & Levin, D.A. 2022 On the synchronisation of three-dimensional shock layer and laminar separation bubble instabilities in hypersonic flow over a double wedge. J. Fluid Mech. 941, A7.CrossRefGoogle Scholar
Schmid, P.J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Schmid, P.J. 2022 Dynamic mode decomposition and its variants. Annu. Rev. Fluid Mech. 54 (1), 225–254.CrossRefGoogle Scholar
Simeonides, G. & Haase, W. 1995 Experimental and computational investigations of hypersonic flow about compression ramps. J. Fluid Mech. 283, 17–42.CrossRefGoogle Scholar
Taira, K., Brunton, S.L., Dawson, S.T.M., Rowley, C.W., Colonius, T., McKeon, B.J., Schmidt, O.T., Gordeyev, S., Theofilis, V. & Ukeiley, L.S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55 (12), 4013–4041.CrossRefGoogle Scholar
Tang, M.-Z., Wang, G., Xie, Z.-X., Zhou, W.-F., Hu, Y.-C. & Yang, Y.-G. 2021 Aerothermodynamic characteristics of hypersonic curved compression ramp flows with bistable states. Phys. Fluids 33 (12), 126106.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
Tobak, M. & Peake, D.J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14 (1), 61–85.CrossRefGoogle Scholar
Tong, F., Tang, Z., Yu, C., Zhu, X. & Li, X. 2017 Numerical analysis of shock wave and supersonic turbulent boundary interaction between adiabatic and cold walls. J. Turbul. 18 (6), 569–588.CrossRefGoogle Scholar
Touber, E. & Sandham, N.D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.CrossRefGoogle Scholar
Tu, J.H., Rowley, C.W., Luchtenburg, D.M., Brunton, S.L. & Kutz, J.N. 2014 On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1 (2), 391–421.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.CrossRefGoogle Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81 (19), 4140–4143.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15 (6), 1517–1534.CrossRefGoogle Scholar
Wedin, H. & Kerswell, R.R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
White, F.M. 2006 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Wu, M. & Martin, M.P. 2007 Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp. AIAA J. 45 (4), 879–889.CrossRefGoogle Scholar
Wu, W., Meneveau, C. & Mittal, R. 2020 Spatio-temporal dynamics of turbulent separation bubbles. J. Fluid Mech. 883, A45.CrossRefGoogle Scholar
Yu, K., Hao, J., Wen, C.-Y. & Xu, J. 2024 Bi-global stability of supersonic backward-facing step flow. J. Fluid Mech. 981, A29.CrossRefGoogle Scholar
Zapryagaev, V.I., Kavun, I.N. & Lipatov, I.I. 2013 Supersonic laminar separated flow structure at a ramp for a free-stream Mach number of 6. Prog. Flight Phys. 5, 349–362.CrossRefGoogle Scholar
Zhang, K. 2020 Hypersonic Curved Compression Inlet and its Inverse Design. Springer.CrossRefGoogle Scholar
Zhou, W.-F., Hu, Y.-C., Tang, M.-Z., Wang, G., Fang, M. & Yang, Y.-G. 2021 Mechanism of separation hysteresis in curved compression ramp. Phys. Fluids 33 (10), 106108.CrossRefGoogle Scholar