Published online by Cambridge University Press: 07 February 2019
The problem of homogeneous isotropic turbulence (HIT) is revisited within the analytical framework of the Navier–Stokes equations, with a view to assessing rigorously the consequences of the scale invariance (an exact property of the Navier–Stokes equations) for any Reynolds number. The analytical development, which is independent of the 1941 (K41) and 1962 (K62) theories of Kolmogorov for HIT for infinitely large Reynolds number, is applied to the transport equations for the second- and third-order moments of the longitudinal velocity increment, 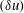 $(\unicode[STIX]{x1D6FF}u)$. Once the normalised equations and the constraints required for complying with the scale-invariance property of the equations are presented, results derived from these equations and constraints are discussed and compared with measurements. It is found that the fluid viscosity,
$(\unicode[STIX]{x1D6FF}u)$. Once the normalised equations and the constraints required for complying with the scale-invariance property of the equations are presented, results derived from these equations and constraints are discussed and compared with measurements. It is found that the fluid viscosity,  $\unicode[STIX]{x1D708}$, and the mean kinetic energy dissipation rate,
$\unicode[STIX]{x1D708}$, and the mean kinetic energy dissipation rate,  $\overline{\unicode[STIX]{x1D716}}$ (the overbar denotes spatial and/or temporal averaging), are the only scaling parameters that make the equations scale-invariant. The analysis further leads to expressions for the distributions of the skewness and the flatness factor of
$\overline{\unicode[STIX]{x1D716}}$ (the overbar denotes spatial and/or temporal averaging), are the only scaling parameters that make the equations scale-invariant. The analysis further leads to expressions for the distributions of the skewness and the flatness factor of 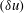 $(\unicode[STIX]{x1D6FF}u)$ and shows that these distributions must exhibit plateaus (of different magnitudes) in the dissipative and inertial ranges, as the Taylor microscale Reynolds number
$(\unicode[STIX]{x1D6FF}u)$ and shows that these distributions must exhibit plateaus (of different magnitudes) in the dissipative and inertial ranges, as the Taylor microscale Reynolds number 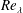 $Re_{\unicode[STIX]{x1D706}}$ increases indefinitely. Also, the skewness and flatness factor of the longitudinal velocity derivative become constant as
$Re_{\unicode[STIX]{x1D706}}$ increases indefinitely. Also, the skewness and flatness factor of the longitudinal velocity derivative become constant as 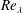 $Re_{\unicode[STIX]{x1D706}}$ increases; this is supported by experimental data. Further, the analysis, backed up by experimental evidence, shows that, beyond the dissipative range, the behaviour of
$Re_{\unicode[STIX]{x1D706}}$ increases; this is supported by experimental data. Further, the analysis, backed up by experimental evidence, shows that, beyond the dissipative range, the behaviour of 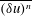 $\overline{(\unicode[STIX]{x1D6FF}u)^{n}}$ with
$\overline{(\unicode[STIX]{x1D6FF}u)^{n}}$ with 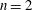 $n=2$, 3 and 4 cannot be represented by a power law of the form
$n=2$, 3 and 4 cannot be represented by a power law of the form 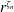 $r^{\unicode[STIX]{x1D701}_{n}}$ when the Reynolds number is finite. It is shown that only when
$r^{\unicode[STIX]{x1D701}_{n}}$ when the Reynolds number is finite. It is shown that only when 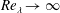 $Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$ can an
$Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$ can an  $n$-thirds law (i.e.
$n$-thirds law (i.e.  $\overline{(\unicode[STIX]{x1D6FF}u)^{n}}\sim r^{\unicode[STIX]{x1D701}_{n}}$, with
$\overline{(\unicode[STIX]{x1D6FF}u)^{n}}\sim r^{\unicode[STIX]{x1D701}_{n}}$, with 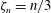 $\unicode[STIX]{x1D701}_{n}=n/3$) emerge, which is consistent with the onset of a scaling range.
$\unicode[STIX]{x1D701}_{n}=n/3$) emerge, which is consistent with the onset of a scaling range.