Published online by Cambridge University Press: 10 September 2018
Spectral energy transfer in a turbulent channel flow is investigated at Reynolds number 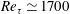 $Re_{\unicode[STIX]{x1D70F}}\simeq 1700$, based on the wall shear velocity and channel half-height, with a particular emphasis on full visualization of triadic wave interactions involved in turbulent transport. As in previous studies, turbulent production is found to be almost uniform, especially over the logarithmic region, and the related spanwise integral length scale is approximately proportional to the distance from the wall. In the logarithmic and outer regions, the energy balance at the integral length scales is mainly formed between production and nonlinear turbulent transport, the latter of which plays the central role in the energy cascade down to the Kolmogorov microscale. While confirming the classical role of the turbulent transport, the triadic wave interaction analysis unveils two new types of scale interaction processes, highly active in the near-wall and the lower logarithmic regions. First, for relatively small energy-containing motions, part of the energy transfer mechanisms from the integral to the adjacent small length scale in the energy cascade is found to be provided by the interactions between larger energy-containing motions. It is subsequently shown that this is related to involvement of large energy-containing motions in skin-friction generation. Second, there exists a non-negligible amount of energy transfer from small to large integral scales in the process of downward energy transfer to the near-wall region. This type of scale interaction is predominant only for the streamwise and spanwise velocity components, and it plays a central role in the formation of the wall-reaching inactive part of large energy-containing motions. A further analysis reveals that this type of scale interaction leads the wall-reaching inactive part to scale in the inner units, consistent with the recent observation. Finally, it is proposed that turbulence production and pressure–strain spectra support the existence of the self-sustaining process as the main turnover dynamics of all the energy-containing motions.
$Re_{\unicode[STIX]{x1D70F}}\simeq 1700$, based on the wall shear velocity and channel half-height, with a particular emphasis on full visualization of triadic wave interactions involved in turbulent transport. As in previous studies, turbulent production is found to be almost uniform, especially over the logarithmic region, and the related spanwise integral length scale is approximately proportional to the distance from the wall. In the logarithmic and outer regions, the energy balance at the integral length scales is mainly formed between production and nonlinear turbulent transport, the latter of which plays the central role in the energy cascade down to the Kolmogorov microscale. While confirming the classical role of the turbulent transport, the triadic wave interaction analysis unveils two new types of scale interaction processes, highly active in the near-wall and the lower logarithmic regions. First, for relatively small energy-containing motions, part of the energy transfer mechanisms from the integral to the adjacent small length scale in the energy cascade is found to be provided by the interactions between larger energy-containing motions. It is subsequently shown that this is related to involvement of large energy-containing motions in skin-friction generation. Second, there exists a non-negligible amount of energy transfer from small to large integral scales in the process of downward energy transfer to the near-wall region. This type of scale interaction is predominant only for the streamwise and spanwise velocity components, and it plays a central role in the formation of the wall-reaching inactive part of large energy-containing motions. A further analysis reveals that this type of scale interaction leads the wall-reaching inactive part to scale in the inner units, consistent with the recent observation. Finally, it is proposed that turbulence production and pressure–strain spectra support the existence of the self-sustaining process as the main turnover dynamics of all the energy-containing motions.