Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T09:58:52.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Satellite formation during bubble transition through an interface between immiscible liquids

Published online by Cambridge University Press:  12 March 2014

E. Q. Li ,
S. A. Al-Otaibi ,
I. U. Vakarelski  and
S. T. Thoroddsen
E. Q. Li
Affiliation:
Division of Physical Sciences and Engineering & Clean Combustion Research Center, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia
S. A. Al-Otaibi
Affiliation:
North Ghawar Producing Department, “Saudi Arabian Oil Company (Saudi Aramco)”, Abqaiq, Saudi Arabia
I. U. Vakarelski
Affiliation:
Division of Physical Sciences and Engineering & Clean Combustion Research Center, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia
S. T. Thoroddsen*
Affiliation:
Division of Physical Sciences and Engineering & Clean Combustion Research Center, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When a bubble rises to an interface between two immiscible liquids, it can pass through the interface, if this is energetically favourable, i.e. the bubble preferring the side of the interface with the lower air–liquid surface tension. Once the intermediate film between the bubble and the interface has drained sufficiently, the bubble makes contact with the interface, forming a triple-line and producing strong capillary waves which travel around the bubble and can pinch off a satellite on the opposite side, akin to the dynamics in the coalescence cascade. We identify the critical Ohnesorge numbers where such satellites are produced and characterize their sizes. The total transition time scales with the bubble size and differential surface tension, while the satellite pinch-off time scales with the capillary-inertial time of the pool liquid, which originally surrounds the bubble. We also use high-speed video imaging to study the motion of the neck of the contact. For low viscosity we show that it grows in time with a power-law exponent between 0.44 and 0.50, with a prefactor modified by the net sum of the three interfacial tensions. 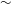Increasing the viscosity of the receiving liquid drop drastically slows down the motion of the triple-line, when the Ohnesorge number exceeds ${\sim }$0.08. This differs qualitatively from the coalescence of two miscible drops of different viscosities, where the lower viscosity sets the coalescence speed. We thereby propose a strong resistance from the triple-line.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Bubble dynamics Interfacial Flows (free surface): Capillary flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , R1
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aarts, D. G. A. L., Lekkerkerker, H. N. W., Guo, H., Wegdam, G. H. & Bonn, D. 2005 Hydrodynamics of droplet coalescence. Phys. Rev. Lett. 95, 164503.Google Scholar
Blanchette, F. & Bigioni, T. P. 2006 Partial coalescence of drops at liquid interfaces. Nat. Phys. 2, 254–257.Google Scholar
Blanchette, F. & Bigioni, T. P. 2009 Dynamics of drop coalescence at fluid interfaces. J. Fluid Mech. 620, 333–352.Google Scholar
Blanchette, F., Messio, L. & Bush, J. W. M. 2009 The influence of surface tension gradients on drop coalescence. Phys. Fluids 21, 072107.Google Scholar
Carlson, A., Bellani, G. & Amberg, G. 2012 Universality in dynamic wetting dominated by contact-line friction. Phys. Rev. E 85, 045302(R).Google ScholarPubMed
Charles, G. E. & Mason, S. G. 1960 The mechanism of partial coalescence of liquid drops at liquid/liquid interfaces. J. Colloid Sci. 15, 105–122.Google Scholar
Chen, X. P., Mandre, S. & Feng, J. J. 2006 Partial coalescence between a drop and a liquid–liquid interface. Phys. Fluids 18, 051705.Google Scholar
Ding, H., Li, E. Q., Zhang, F. H., Sui, Y., Spelt, P. D. M. & Thoroddsen, S. T. 2012 Propagation of capillary waves and ejection of small droplets in rapid droplet spreading. J. Fluid Mech. 697, 92–114.Google Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Gilet, T., Mulleners, K., Lecomte, J. P., Vandewalle, N. & Dorbolo, S. 2007 Critical parameters for the partial coalescence of a droplet. Phys. Rev. E 75, 036303.Google Scholar
Honey, E. M. & Kavehpour, H. P. 2006 Astonishing life of a coalescing drop on a free surface. Phys. Rev. E 73.Google Scholar
Mohamed-Kassim, Z. & Longmire, E. K. 2004 Drop coalescence through a liquid/liquid interface. Phys. Fluids 16, 2170–2181.Google Scholar
Neeson, M. J., Tabor, R. F., Grieser, F., Dagastine, R. R. & Chan, D. Y. C. 2012 Compound sessile drops. Soft Matt. 8, 11042–11050.Google Scholar
Ohnishi, M., Azuma, H. & Straub, J. 1999 Study on secondary bubble creation induced by bubble coalescence. Adv. Space Res. 24, 1331–1336.Google Scholar
Paulsen, J. D., Burton, J. C. & Nagel, S. R. 2011 Viscous to inertial crossover in liquid drop coalescence. Phys. Rev. Lett. 106, 114501.Google Scholar
Paulsen, J. D., Burton, J. C., Nagel, S. R., Appathuri, A., Harris, M. T. & Basaran, O. A. 2012 The initial regime of coalescence: the inexorable resistance of inertia. Proc. Natl Acad. Sci. USA 109, 6857–6861.Google Scholar
Ray, B., Biswas, G. & Sharma, A. 2010 Generation of secondary droplets in coalescence of a drop at a liquid–liquid interface. J. Fluid Mech. 655, 72–104.Google Scholar
Rioboo, R., Adao, M. H., Voue, M. & De Coninck, J. 2006 Experimental evidence of liquid drop break-up in complete wetting experiments. J. Mater. Sci. 41, 5068–5080.Google Scholar
Roux, D. C. D. & Cooper-White, J. J. 2004 Dynamics of water spreading on a glass surface. J. Colloid Interface Sci. 277, 424–436.Google Scholar
Smedley, G. & Coles, D. 1990 Some transparent immiscible liquid pairs. J. Colloid Interface Sci. 138, 42–60.Google Scholar
Sprittles, J. E. & Shikhmurzaev, Y. D. 2012 Coalescence of liquid drops: different models versus experiment. Phys. Fluids 24, 122105.CrossRefGoogle Scholar
Thoraval, M.-J. & Thoroddsen, S. T. 2013 Contraction of an air disk caught between two different liquids. Phys. Rev. E 88, 061001(R).Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K. & Ootsuka, N. 2005a On the coalescence speed of bubbles. Phys. Fluids 17, 071703.Google Scholar
Thoroddsen, S. T., Qian, B., Etoh, T. G. & Takehara, K. 2007 The initial coalescence of miscible drops. Phys. Fluids 19, 072110.CrossRefGoogle Scholar
Thoroddsen, S. T. & Takehara, K. 2000 The coalescence-cascade of a drop. Phys. Fluids 12, 1257–1265.Google Scholar
Thoroddsen, S. T., Takehara, K. & Etoh, T. G. 2005b The coalescence speed of a pendent and a sessile drop. J. Fluid Mech. 527, 85–114.Google Scholar
Winkels, K. G., Weijs, J. H., Eddi, A. & Snoeijer, J. H. 2012 Initial spreading of low-viscosity drops on partially wetting surfaces. Phys. Rev. E 85, 055301(R).Google Scholar
Wu, M., Cubaud, T. & Ho, C.-M. 2004 Scaling law in liquid drop coalescence driven by surface tension. Phys. Fluids 16, L51.Google Scholar
Yue, P. T., Zhou, C. F. & Feng, J. J. 2006 A computational study of the coalescence between a drop and an interface in Newtonian and viscoelastic fluids. Phys. Fluids 18, 102102.Google Scholar
Zhang, F. H., Li, E. Q. & Thoroddsen, S. T. 2009 Satellite formation during coalescence of unequal size drops. Phys. Rev. Lett. 102, 104502.Google Scholar
Zhang, F. H. & Thoroddsen, S. T. 2008 Satellite generation during bubble coalescence. Phys. Fluids 20, 022104.Google Scholar
Supplementary material: PDF

Li et al. supplementary material

Supplementary data

Download Li et al. supplementary material(PDF)
PDF 29 KB