Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T13:18:45.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotational kinematics of large cylindrical particles in turbulence

Published online by Cambridge University Press:  20 February 2017

Ankur D. Bordoloi Open the ORCID record for Ankur D. Bordoloi [Opens in a new window]  and
Evan Variano
Ankur D. Bordoloi*
Affiliation:
Department of Civil and Environmental Engineering, University of California Berkeley, Berkeley, CA 94720, USA
Evan Variano
Affiliation:
Department of Civil and Environmental Engineering, University of California Berkeley, Berkeley, CA 94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

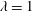The rotational kinematics of inertial cylinders in homogeneous isotropic turbulence is investigated via laboratory experiments. The effects of particle size and shape on rotation statistics are measured for near-neutrally buoyant particles whose sizes are within the inertial subrange of turbulence. To examine the effects of particle size, three right-circular cylinders (aspect ratio $\unicode[STIX]{x1D706}=1$) are considered, with size 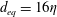$d_{eq}=16\unicode[STIX]{x1D702}$, 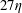$27\unicode[STIX]{x1D702}$ and 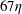$67\unicode[STIX]{x1D702}$. Here, 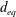$d_{eq}$ is the diameter of a sphere whose volume is equal to that of the particle and 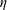$\unicode[STIX]{x1D702}$ is the Kolmogorov length scale. Results show that the variance of the particle rotation rate follows a 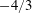$-4/3$ power-law scaling with respect to 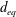$d_{eq}$. To examine the effect of particle shape, two cylinders with identical volumes and different aspect ratios (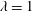$\unicode[STIX]{x1D706}=1$ and 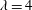$\unicode[STIX]{x1D706}=4$) are measured. Their motion also scales with 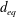$d_{eq}$ regardless of shape. Simultaneous measurements of orientation and rotation for 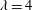$\unicode[STIX]{x1D706}=4$ particles allows a decomposition of rotation along the primary axes of each particle. This analysis shows that there is no preference for rotation about a particle’s symmetry axis, unlike the preference displayed by sub-Kolmogorov-scale particles in previous studies.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 199 - 222
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellani, G., Byron, M. L., Collignon, A. G., Meyer, C. R. & Variano, E. A. 2012 Shape effects on turbulent modulation by large nearly neutrally buoyant particles. J. Fluid Mech. 712, 41–60.Google Scholar
Bellani, G. & Variano, E. 2014 Homogeneity and isotropy in a laboratory turbulent flow. Exp. Fluids 55 (1646), 1–12.Google Scholar
Burton, T. M. & Eaton, J. K. 2005 Fully resolved simulations of particle–turbulence interaction. J. Fluid Mech. 545, 67–111.CrossRefGoogle Scholar
Byron, M.2015 The rotation and translation of non-spherical particles in homogeneous isotropic turbulence. PhD thesis, University of California, Berkeley.Google Scholar
Byron, M., Einarsson, J., Gustavsson, K., Voth, G., Mehlig, B. & Variano, E. 2015 Shape-dependence of particle rotation in isotropic turbulence. Phys. Fluids 27, 035101.Google Scholar
Byron, M. L. & Variano, E. A. 2013 Refractive-index-matched hydrogel materials for measuring flow–structure interactions. Exp. Fluids 54, 1456.Google Scholar
Capecelatro, J. & Desjardins, O. 2015 Mass loading effects on turbulence modulation by particle clustering in dilute and moderately dilute channel flows. Trans. ASME J. Fluids Engng 137 (11), 111102.Google Scholar
Challabotla, N. R., Nilsen, C. & Andersson, H. I. 2015a On rotational dynamics of inertial disks in creeping shear flow. Phys. Lett. A 379 (3), 157–162.Google Scholar
Challabotla, N. R., Zhao, L. & Andersson, H. I. 2015b Orientation and rotation of inertial disk particles in wall turbulence. J. Fluid Mech. 766, R2.Google Scholar
Chevillard, L. & Meneveau, C. 2013 Orientation dynamics of small, triaxial–ellipsoidal particles in isotropic turbulence. J. Fluid Mech. 737, 571–596.Google Scholar
Cisse, M., Saw, E. W., Gilbert, M., Bodenschatz, E. & Bec, J. 2015 Turbulence attenuation by large neutrally buoyant particles. Phys. Fluids 27, 061702.CrossRefGoogle Scholar
De Lillo, F., Cencini, M., Durham, W. M., Barry, M., Stocker, R., Climent, E. & Boffetta, G. 2014 Turbulent fluid acceleration generates clusters of gyrotactic microorganisms. Phys. Rev. Lett. 112 (4), 044502.Google Scholar
Efron, B. & Tibshirani, R. J. 1993 An Introduction to the Bootstrap: Monographs on Statistics & Applied Probability, 1st edn, vol. 57. Chapman & Hall/CRC.Google Scholar
Einarsson, J., Candelier, F., Lundell, F., Angilella, J. R. & Mehlig, B. 2015 Rotation of a spheroid in a simple shear at small Reynolds number. Phys. Fluids 27, 063301.CrossRefGoogle Scholar
Elghobashi, S. 2003 On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 15, 315–329.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two way interaction between homogeneous turbulence and dispersed solid particles. I. Turbulence modification. Phys. Fluids A 5, 1790–1801.Google Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.CrossRefGoogle Scholar
Ganser, G. H. 1983 A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 77, 143.Google Scholar
Gustavsson, K., Einarsson, J. & Mehlig, B. 2014 Tumbling of small axisymmetric particles in random and turbulent flows. Phys. Rev. Lett. 112 (1), 014501.Google Scholar
Gustavsson, K., Berglund, F., Jonsson, P. R. & Mehlig, B. 2016 Preferential sampling and small-scale clustering of gyrotactic microswimmers in turbulence. Phys. Rev. Lett. 116, 108104.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 161–179.Google Scholar
Leith, D. 1987 Drag on non-spherical objects. Aerosol Sci. Technol. 6, 153–161.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study lagrangian evolution of velocity increments in turbulence. J. Turbul. 9, N31.CrossRefGoogle Scholar
Loth, E. 2008 Drag of non-spherical solid particles of regular and irregular shape. Powder Technol. 182, 342–353.Google Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.Google Scholar
Lundell, F. & Carlsson, A. 2010 Heavy ellipsoids in creeping shear flow: transitions of the particle rotation rate and orbit shape. Phys. Rev. E 81, 016323.Google Scholar
Marchioli, C., Fantoni, M. & Soldati, A. 2010 Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow. Phys. Fluids 22 (3), 033301.Google Scholar
Marcus, G. G., Parsa, S., Kramel, S., Ni, R. & Voth, G. A. 2014 Measurements of the solid-body rotation of anisotropic particles in 3d turbulence. New J. Phys. 16, 102001.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2007 Particle spin in a turbulent shear flow. Phys. Fluids 19, 078109.Google Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008 Dynamics of prolate ellipsoidal particles in a turbulent channel flow. Phys. Fluids 20, 0933202.Google Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109 (13), 134501.Google Scholar
Parsa, S. & Voth, G. A. 2014 Inertial range scaling in rotations of long rods in turbulence. Phys. Rev. Lett. 112 (2), 024501.Google Scholar
Pérez-Alvarado, A., Mydlarski, L. & Gaskin, S. 2016 Effect of the driving algorithm on the turbulence generated by a random jet array. Exp. Fluids 57 (20), 1–15.Google Scholar
Pope, S. B. 2000 Turbulent Flows, 1st edn. Cambridge University Press.Google Scholar
Pumir, A. & Wilkinson, M. 2011 Orientation statistics of small particles in turbulence. New J. Phys. 13, 093030.Google Scholar
Qureshi, N. M., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99, 184502.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide (Experimental Fluid Mechanics), 2nd edn. Springer.Google Scholar
Rosen, T., Do-Quang, M., Aidun, C. K. & Lundell, F. 2015 The dynamical states of a prolate spheroidal particle suspended in shear flow as a consequence of particle and fluid inertia. J. Fluid Mech. 771, 115–158.Google Scholar
Shin, M. & Koch, D. L. 2005 Rotational and translational dispersion of fibres in isotropic turbulent flows. J. Fluid Mech. 540, 143.Google Scholar
Squires, K. D. & Eaton, J. K. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A 2, 1191–1203.Google Scholar
Tanaka, T. & Eaton, J. K. 2008 Classification of turbulence modification by dispersed spheres using a novel dimensionless number. Phys. Rev. Lett. 101 (11), 114502.Google Scholar
Variano, E. A. & Cowen, E. A. 2008 A random-jet-stirred turbulence tank. J. Fluid Mech. 604, 1–32.Google Scholar
Xu, H. & Bodenschatz, E. 2008 Motion of inertial particles with size larger than Kolmogorov scale in turbulent flows. Physica D 237, 2095–2100.Google Scholar
Yeo, K., Dong, S., Climent, E. & Maxey, M. R. 2010 Modulation of homogeneous turbulence seeded with finite size bubbles or particles. Intl J. Multiphase Flow 36 (3), 221–233.Google Scholar
Yu, H., Kanov, K., Perlman, E., Graham, J., Frederix, E., Burns, R., Szalay, A., Eyink, G. & Meneveau, C. 2012 Studying Lagrangian dynamics of turbulence using on-demand fluid particle tracking in a public turbulence database. J. Turbul. 13, N12.Google Scholar
Zhang, H., Ahmadi, G., Fan, F. G. & Mclaughlin, J. B. 2001 Ellipsoidal particles transport and deposition in turbulent channel flows. Intl J. Multiphase Flow 27 (6), 971–1009.Google Scholar
Zhao, F., George, W. K. & van Wachem, B. G. M. 2015a Four-way coupled simulations of small particles in turbulent channel flow: the effects of particle shape and Stokes number. Phys. Fluids 27 (8), 083301.Google Scholar
Zhao, L., Challabotla, N. R., Andersson, H. I. & Variano, E. A. 2015b Rotation of nonspherical particles in turbulent channel flow. Phys. Rev. Lett. 115, 244501.Google Scholar
Zhao, L., Marchioli, C. & Andersson, H. 2014 Slip velocity of rigid fibers in turbulent channel flow. Phys. Fluids 26 (6), 063302.Google Scholar