Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-09T21:59:49.937Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotation of spheroidal particles in Couette flows

Published online by Cambridge University Press:  05 January 2012

Haibo Huang ,
Xin Yang ,
Manfred Krafczyk  and
Xi-Yun Lu
Haibo Huang*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, China Institute for Computational Modelling in Civil Engineering, Technische Universität, Braunschweig 38106, Germany
Xin Yang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, China
Manfred Krafczyk
Affiliation:
Institute for Computational Modelling in Civil Engineering, Technische Universität, Braunschweig 38106, Germany
Xi-Yun Lu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

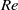The rotation of a neutrally buoyant spheroidal particle in a Couette flow is studied by a multi-relaxation-time (MRT) lattice Boltzmann method. We find several new periodic and steady rotation modes for a prolate spheroid for Reynolds numbers () exceeding 305. The simulations cover the regime up to 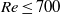. The rotational behaviour of the spheroid appears to be not only sensitive to the Reynolds number but also to its initial orientation. We discuss the effects of initial orientation in detail. For 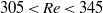we find that the prolate spheroid reaches a periodic mode characterized by precession and nutation around an inclined axis which is located close to the middle plane where the velocity is zero. For 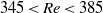, the prolate spheroid precesses around the vorticity direction with a nutation. For 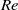close to the critical 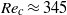, a period-doubling phenomenon is observed. We also identify a motionless mode at higher Reynolds numbers (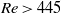) for the prolate spheroid. For the oblate spheroid the dynamic equilibrium modes found are log rolling, inclined rolling and different steady states for 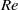increasing from 0 to 520. The initial-orientation effects are studied by simulations of 57 evenly distributed initial orientations for each 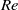investigated. Only one mode is found for the prolate spheroid for 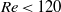and 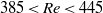. In other 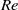regimes, more than one mode is possible and the final mode is sensitive to the initial orientation. However, the oblate spheroid dynamics are insensitive to its initial orientation.

JFM classification

Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 692 , 10 February 2012 , pp. 369 - 394
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Aidun, C. K., Lu, Y. & Ding, E. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.CrossRefGoogle Scholar
2.Bouzidi, M., Firdaouss, M. & Lallemand, P. 2001 Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 13, 3452–3459.CrossRefGoogle Scholar
3.Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.CrossRefGoogle Scholar
4.Ding, E. & Aidun, C. K. 2000 The dynamics and scaling law for particles suspended in shear flow with inertia. J. Fluid Mech. 423, 317–344.CrossRefGoogle Scholar
5.Einstein, A. 1905 Investigations on the theory of Brownian movement. Ann. Phys. 17, 549–560.CrossRefGoogle Scholar
6.Feng, J. & Joseph, D. D. 1995 The unsteady motion of solid bodies in creeping flows. J. Fluid Mech. 303, 83–102.CrossRefGoogle Scholar
7.Feng, Z.-G. & Michaelides, E. E. 2004 The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems. J. Comput. Phys. 195, 602–628.CrossRefGoogle Scholar
8.Guo, Z. L., Zheng, C. G. & Shi, B. C. 2002 An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 14, 2007–2010.CrossRefGoogle Scholar
9.Harper, E. Y. & Chang, I.-D. 1968 Maximum dissipation resulting from lift in a slow viscous shear flow. J. Fluid Mech. 33, 209–225.CrossRefGoogle Scholar
10.He, X., Zou, Q., Luo, L.-S. & Dembo, M. 1997 Analytic solutions of simple flows and analysis of non-slip bundary conditions for the lattice Boltzmann BGK model. J. Stat. Phys. 87, 115–136.CrossRefGoogle Scholar
11.d’Humiéres, D., Ginzburg, I., Krafczyk, M., Lallemand, P. & Luo, L.-S. 2002 Multiple-relaxation-time lattice Boltzmann models in three dimensions. Phil. Trans. R. Soc. Lond. A 360, 437–451.CrossRefGoogle ScholarPubMed
12.Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
13.Karnis, A., Goldsmith, H. L. & Mason, S. G. 1963 Axial migration of particles in Poiseuille flow. Nature 200, 159–160.CrossRefGoogle Scholar
14.Ladd, A. J. C. 1994a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.CrossRefGoogle Scholar
15.Ladd, A. J. C. 1994b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.CrossRefGoogle Scholar
16.Lallemand, P. & Luo, L.-S. 2003 Lattice Boltzmann method for moving boundaries. J. Comput. Phys. 184, 406–421.CrossRefGoogle Scholar
17.Leal, L. G. 1975 The low motion of slender fluid rod-like particles in a second order fluid. J. Fluid Mech. 69, 305–337.CrossRefGoogle Scholar
18.Leal, L. G. 1980 Particle motion in a viscous fluid. Annu. Rev. Fluid Mech. 12, 435–476.CrossRefGoogle Scholar
19.Mei, R., Yu, D., Shyy, W. & Luo, L.-S. 2002 Force evaluation in the lattice Boltzmann method involving curved geometry. Phy. Rev. E 65, 041203.CrossRefGoogle ScholarPubMed
20.Qi, D. 1999 Lattice-Boltzmann simulations of particles in non-zero-Reynolds-number flows. J. Fluid Mech. 385, 41–62.CrossRefGoogle Scholar
21.Qi, D. & Luo, L.-S. 2002 Transitions in rotations of a non-spherical particle in a three-dimensional moderate Reynolds number Couette flow. Phys. Fluids 14, 4440–4443.CrossRefGoogle Scholar
22.Qi, D. & Luo, L.-S. 2003 Rotational and orientational behaviour of a three-dimensional spheroidal particles in Couette flows. J. Fluid Mech. 477, 201–213.CrossRefGoogle Scholar
23.Taylor, G. I. 1923 The motion of ellipsoidal particles in a viscous fluid. Proc. R. Soc. Lond. A 102, 58–61.Google Scholar
24.Yu, Z., Phan-Thien, N. & Tanner, R. I. 2007 Rotation of a spheroid in a Couette flow at moderate Reynolds numbers. Phys. Rev. E 76, 026310.CrossRefGoogle Scholar
25.Zettner, C. M. & Yoda, M. 2001 Moderate-aspect-ratio elliptical cylinders in simple shear with inertia. J. Fluid Mech. 442, 241–266.CrossRefGoogle Scholar