Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T22:06:22.221Z Has data issue: false hasContentIssue false
  • English
  • Français

Role of the basin boundary conditions in gravity wave turbulence

Published online by Cambridge University Press:  16 September 2015

L. Deike ,
B. Miquel ,
P. Gutiérrez ,
T. Jamin ,
B. Semin ,
M. Berhanu ,
E. Falcon  and
F. Bonnefoy
L. Deike
Affiliation:
Laboratoire Matière et Systèmes Complexes, UMR 7057 CNRS, Université Paris Diderot, Sorbonne Paris Cité, 75013 Paris, France
B. Miquel
Affiliation:
Laboratoire de Physique Statistique, Ecole Normale Supérieure, UPMC Univ Paris 06, Université Paris Diderot, CNRS, 24 rue Lhomond, 75005 Paris, France
P. Gutiérrez
Affiliation:
Laboratoire SPHYNX, SPEC, DSM, UMR 3680 CNRS, CEA-Saclay, 91191 Gif-sur-Yvette, France
T. Jamin
Affiliation:
Laboratoire Matière et Systèmes Complexes, UMR 7057 CNRS, Université Paris Diderot, Sorbonne Paris Cité, 75013 Paris, France
B. Semin
Affiliation:
Laboratoire de Physique Statistique, Ecole Normale Supérieure, UPMC Univ Paris 06, Université Paris Diderot, CNRS, 24 rue Lhomond, 75005 Paris, France
M. Berhanu
Affiliation:
Laboratoire Matière et Systèmes Complexes, UMR 7057 CNRS, Université Paris Diderot, Sorbonne Paris Cité, 75013 Paris, France
E. Falcon*
Affiliation:
Laboratoire Matière et Systèmes Complexes, UMR 7057 CNRS, Université Paris Diderot, Sorbonne Paris Cité, 75013 Paris, France
F. Bonnefoy
Affiliation:
Laboratoire LHEEA, UMR 6598 CNRS, Ecole Centrale de Nantes, 44321 Nantes, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Gravity wave turbulence is investigated experimentally in a large wave basin in which irregular waves are generated unidirectionally. The roles of the basin boundary conditions (absorbing or reflecting) and of the forcing properties are investigated. To that purpose, an absorbing sloping beach opposite the wavemaker can be replaced by a reflecting vertical wall. We observe that the wave field properties depend strongly on these boundary conditions. A quasi-one-dimensional field of nonlinear waves propagates towards the beach, where they are damped whereas a more multidirectional wave field is observed with the wall. 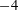In both cases, the wave spectrum scales as a frequency power law with an exponent that increases continuously with the forcing amplitude up to a value close to $-4$. The physical mechanisms involved most likely differ with the boundary condition used, but cannot be easily discriminated with only temporal measurements. We also studied freely decaying gravity wave turbulence in the closed basin. No self-similar decay of the spectrum is observed, whereas its Fourier modes decay first as a time power law due to nonlinear mechanisms, and then exponentially due to linear viscous damping. We estimate the linear, nonlinear and dissipative time scales to test the time scale separation that highlights the important role of a large-scale Fourier mode. By estimation of the mean energy flux from the initial decay of wave energy, the Kolmogorov–Zakharov constant of the weak turbulence theory is evaluated and found to be compatible with a recently obtained theoretical value.

JFM classification

Turbulent Flows: Intermittency Waves/Free-surface Flows: Surface gravity waves Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 196 - 225
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Scripps Institution of Oceanography, University of California San Diego, 9500 Gilman DriveLa Jolla, CA 92093, USA.

References

Aubourg, Q. & Mordant, N. 2015 Nonlocal resonances in weak turbulence of gravity–capillary waves. Phys. Rev. Lett. 114, 144501.Google Scholar
Badulin, S. I., Pushkarev, A. N., Resio, D. & Zakharov, V. E. 2005 Self-similarity of wind-driven seas. Nonlinear Process. Geophys. 12, 891–945.Google Scholar
Banner, M. L. 1990 Equilibrium spectra of wind waves. J. Phys. Oceanogr. 20, 966–984.2.0.CO;2>CrossRefGoogle Scholar
Bedard, R., Lukaschuk, S. & Nazarenko, S. 2013a Gravity wave turbulence in a large flume. In Advances in Wave Turbulence (ed. Shrira, V. & Nazarenko, S.). World Scientific.Google Scholar
Bedard, R., Nazarenko, S. & Lukaschuk, S. 2013b Non-stationary regimes of surface gravity wave turbulence. JETP Lett. 87, 529–535.Google Scholar
Berhanu, M. & Falcon, E. 2013 Space-time resolved capillary wave turbulence. Phys. Rev. E 89, 033003.Google Scholar
Bonnefoy, F.2005 Modélisation expérimentale et numérique des états de mer complexes. PhD thesis, Université de Nantes et Ecole Centrale de Nantes.Google Scholar
Cobelli, P., Maurel, A., Pagneux, V. & Petitjeans, P. 2009 Global measurement of water waves by Fourier transform profilometry. Exp. Fluids 46, 1037–1047.CrossRefGoogle Scholar
Cobelli, P., Przadka, A., Petitjeans, P., Lagubeau, G., Pagneux, V. & Maurel, A. 2011 Different regimes for water wave turbulence. Phys. Rev. Lett. 107, 214503.CrossRefGoogle ScholarPubMed
Connaughton, C., Nazarenko, S. & Newell, A. C. 2003 Dimensional analysis and weak turbulence. Physica D 184, 86–97.Google Scholar
Deike, L., Bacri, J. C. & Falcon, E. 2013 Nonlinear waves on the surface of a fluid covered by an elastic sheet. J. Fluid Mech. 733, 394–413.Google Scholar
Deike, L., Berhanu, M. & Falcon, E. 2012 Decay of capillary wave turbulence. Phys. Rev. E 85, 066311.CrossRefGoogle ScholarPubMed
Deike, L., Berhanu, M. & Falcon, E. 2014a Energy flux measurement from the dissipated energy in capillary wave turbulence. Phys. Rev. E 89, 023003.CrossRefGoogle ScholarPubMed
Deike, L., Fuster, D., Berhanu, M. & Falcon, E. 2014b Direct numerical simulations of capillary wave turbulence. Phys. Rev. Lett. 112, 234501.CrossRefGoogle ScholarPubMed
Deike, L., Laroche, C. & Falcon, E. 2011 Experimental study of the inverse cascade in gravity wave turbulence. Europhys. Lett. 96, 34004.CrossRefGoogle Scholar
Denissenko, P., Lukaschuk, S. & Nazarenko, S. 2007 Gravity wave turbulence in a laboratory flume. Phys. Rev. Lett. 99, 014501.Google Scholar
Donelan, M. A., Hamilton, J. & Hui, W. H. 1985 Directional spectra of wind-generated waves. Phil. Trans. R. Soc. Lond. A 315, 509–562.Google Scholar
van Dorn, W. G. 1966 Boundary dissipation of oscillatory waves. J. Fluid Mech. 24, 769–779.CrossRefGoogle Scholar
Dyachenko, A. I., Korotkevich, A. O. & Zakharov, V. E. 2004 Weak turbulent Kolmogorov spectrum for surface gravity waves. Phys. Rev. Lett. 92, 134501.Google Scholar
Falcon, E., Fauve, S. & Laroche, S. 2007a Observation of intermittency in wave turbulence. Phys. Rev. Lett. 98, 154501.Google Scholar
Falcon, E. & Laroche, C. 2011 observation of depth-induced properties in wave turbulence on the surface of a fluid. Europhys. Lett. 95, 34003.Google Scholar
Falcon, E., Laroche, C. & Fauve, S. 2007b Observation of gravity–capillary wave turbulence. Phys. Rev. Lett. 98, 094503.Google ScholarPubMed
Falcon, E., Roux, S. G. & Audit, B. 2010a Revealing intermittency in experimental data with steep power spectra. Europhys. Lett. 90, 5007.Google Scholar
Falcon, E., Roux, S. G. & Laroche, S. 2010b On the origin of intermittency in wave turbulence. Europhys. Lett. 90, 34005.Google Scholar
Falkovich, G. E., Shapiro, I. Y. & Shtilman, L. 1995 Decay turbulence of capillary waves. Europhys. Lett. 29, 1–6.Google Scholar
Forristall, G. Z. 1981 Measurements of a saturated range in ocean wave spectra. J. Geophys. Res. 86, 8075–8084.CrossRefGoogle Scholar
Forristall, G. Z. J. 2000 Wave crest distributions: observations and second-order theory. J. Phys. Oceanogr. 30, 1931–1943.Google Scholar
Gagnaire-Renou, E., Benoit, M. & Badulin, S. I. 2011 On weakly turbulent scaling of wind sea in simulations of fetch-limited growth. J. Fluid Mech. 669, 178–213.Google Scholar
Henderson, D. M. & Segur, H. 2013 The role of dissipation in the evolution of ocean swell. J. Geophys. Res. 118, 5074–5091.Google Scholar
Herbert, E., Mordant, N. & Falcon, E. 2010 Observation of the nonlinear dispersion relation and spatial statistics of wave turbulence on the surface of a fluid. Phys. Rev. Lett. 105, 144502.Google Scholar
Huang, N. E., Long, S. R., Tung, C.-C., Yuen, Y. & Bliven, L. 1981 A unified two-parameter wave spectral model for a general sea state. J. Fluid Mech. 112, 203–224.Google Scholar
Humbert, T., Cadot, O., Düring, G., Josserand, C., Rica, S. & Touzé, C. 2013 Wave turbulence in vibrating plates: the effect of damping. Europhys. Lett. 102, 30002.Google Scholar
Hwang, P. A., Wang, D. W., Walsh, E. J., Krabill, W. B. & Swift, R. N. 2000 Airbone measurements of the wavenumber spectra of ocean surface waves. Part I. Spectral slope and dimensionless spectral coefficient. J. Phys. Oceanogr. 30, 2753–2767.Google Scholar
Issenmann, B. & Falcon, E. 2013 Gravity wave turbulence revealed by horizontal vibrations of the container. Phys. Rev. E 87, 011001(R).CrossRefGoogle ScholarPubMed
Janssen, P. 2004 The Interaction of Ocean Waves and Wind. Cambridge University Press.Google Scholar
Kahma, K. K. 1981 A study of the growth of the wave spectrum with fetch. J. Phys. Oceanogr. 11, 1503–1515.Google Scholar
Kartashova, E. 1998 Wave resonances in systems with discrete spectra. In Nonlinear Waves and Weak Turbulence (ed. Zakharov, V. E.), American Mathematical Society Translations, Series 2, vol. 182, pp. 95–129. American Mathematical Society.Google Scholar
Kitaigorodskii, S. A. 1983 On the theory of the equilibrium range in the spectrum of wind-generated gravity waves. J. Phys. Oceanogr. 13, 816–827.Google Scholar
Kolmakov, G. V., Levchenko, A. A., Brazhnikov, M. Yu., Mezhov-Deglin, L. P., Silchenko, A. N. & McClintock, P. V. E. 2004 Quasiadiabatic decay of capillary turbulence on the charged surface of liquid hydrogen. Phys. Rev. Lett. 93, 074501.Google Scholar
Komen, G. J., Cavaleri, L., Donelan, M., Hasselmann, K., Hasselmann, H. & Janssen, P. A. E. M. 1994 Dynamics and Modeling of Ocean Waves. Cambridge University Press.Google Scholar
Korotkevich, A. O., Pushkarev, A. N., Resio, D. & Zakharov, V. E. 2008 Numerical verification of the weak turbulent model for swell evolution. Eur. J. Mech. (B/Fluids) 27, 361–387.Google Scholar
Korotkevitch, A. O. 2008 Simultaneous numerical simulation of direct inverse cascades in wave turbulence. Phys. Rev. Lett. 101, 074504.Google Scholar
Kuznetsov, E. A. 2004 Turbulence spectra generated by singularities. JETP Lett. 80, 83–89.Google Scholar
Lamb, H. 1932 Hydrodynamics. Springer.Google Scholar
Liu, P. C. 1989 On the slope of the equilibrium range in the frequency spectrum of wind waves. J. Geophys. Res. 94, 5017–5023.Google Scholar
Long, C. E. & Resio, D. T. 2007 Wind wave spectral observations in Currituck Sound, North Carolina. J. Geophys. Res. 112, C05001.Google Scholar
Lvov, Y., Nazarenko, S. & Pokorni 2006 Discreteness and its effect on water–wave turbulence. Physica D 218, 24–35.Google Scholar
Melville, W. K., Veron, F. & White, C. J. 2002 The velocity field under breaking waves: coherent structures and turbulence. J. Fluid Mech. 454, 203–233.Google Scholar
Miles, J. W. 1967 Surface-wave damping in closed basins. Proc. R. Soc. Lond. A 297, 459–475.Google Scholar
Miquel, B., Alexakis, A. & Mordant, N. 2014 Role of dissipation in flexural wave turbulence: from experimental spectrum to Kolmogorov–Zakharov spectrum. Phys. Rev. E 89, 062925.CrossRefGoogle ScholarPubMed
Miquel, B. & Mordant, N. 2011a Nonlinear dynamics of flexural wave turbulence. Phys. Rev. E 84, 066607.Google Scholar
Miquel, B. & Mordant, N. 2011b Nonstationary wave turbulence in an elastic plate. Phys. Rev. Lett. 107, 034501.Google Scholar
Moisy, F., Rabaud, M. & Salsac, K. 2009 A synthetic schlieren method for the measurement of the topography of a liquid interface. Exp. Fluids 46, 1021–1036.Google Scholar
Nazarenko, S. 2006 Sandpile behaviour in discrete water–wave turbulence. J. Stat. Mech. Theory E L02002.Google Scholar
Nazarenko, S. 2011 Wave Turbulence. Springer.Google Scholar
Nazarenko, S., Lukaschuk, S., McLelland, S. & Denissenko, P. 2010 Statistics of surface gravity wave turbulence in the space and time domains. J. Fluid Mech. 642, 395–420.Google Scholar
Newell, A.C. & Rumpf, B. 2011 Wave turbulence. Annu. Rev. Fluid Mech. 43, 59–78.Google Scholar
Newell, A. C. & Zakharov, V. E. 1992 Rough sea foam. Phys. Rev. Lett. 69, 1149–1151.Google Scholar
Ochi, M. K. 1998 Ocean Waves. Cambridge University Press.Google Scholar
Onorato, M., Cavaleri, L., Fouques, S., Gramstad, O., Janssen, P. A. E. M., Monbaliu, J., Osborne, A. R., Pakozdi, C., Serio, M. & Stansberg, C. T. et al. 2009 Statistical properties of mechanically generated surface gravity waves: a laboratory experiment in a three-dimensional wave basin. J. Fluid Mech. 627, 235–257.Google Scholar
Onorato, M., Osborne, A. R., Serio, M., Cavaleri, L., Brandini, C. & Stansberg, C. T. 2004 Observation of strongly non-Gaussian statistics for random sea surface gravity waves in wave flume experiments. Phys. Rev. E 70, 067302.Google Scholar
Onorato, M., Osborne, A. R., Serio, M., Resio, D., Pushkarev, A., Zakharov, V. E. & Brandini, C. 2002 Freely decaying weak turbulence for sea surface gravity waves. Phys. Rev. Lett. 89, 144501.Google Scholar
Pan, Y. & Yue, D. K. P. 2014 Direct numerical investigation of turbulence of capillary waves. Phys. Rev. Lett. 113, 094501.CrossRefGoogle ScholarPubMed
Perlin, M., Choi, W. & Tian, Z. 2013 Breaking waves in deep and intermediate waters. Annu. Rev. Fluid Mech. 45, 115–145.Google Scholar
Phillips, O. M. 1958a The equilibrium range in the spectrum of wind-generated waves. J. Fluid Mech. 4, 426–434.Google Scholar
Phillips, O. M. 1958b Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 156, 505–531.Google Scholar
Pope, S. B. 2006 Turbulent Flows. Cambridge University Press.Google Scholar
Pushkarev, A., Resio, D. & Zakharov, V. 2003 Weak turbulent approach to the wind-generated gravity sea waves. Physica D 184, 29–63.Google Scholar
Romero, L. & Melville, W. K. 2010 Airborne observations of fetch-limited waves in the Gulf of Tehuantepec. J. Phys. Oceanogr. 40, 441–465.Google Scholar
Socquet-Juglard, H., Dysthe, K., Trulsen, K., Krogstad, H. E. & Liu, J. 2005 Probability distributions of surface gravity waves during spectral changes. J. Fluid. Mech. 542, 195–216.Google Scholar
Tayfun, M. A. 1980 Narrow-band nonlinear sea waves. J. Geophys. Res. 85, 1548–1552.Google Scholar
Toba, Y. 1973 Local balance in the air–sea boundary processes. III. On the spectrum of wind waves. J. Oceanogr. Soc. Japan 29, 209–220.Google Scholar
WISEGroup 2007 Wave modelling – the state of the art. Prog. Oceanogr. 75, 603–674.Google Scholar
Wright, W. B., Budakian, R. & Putterman, S. J. 1996 Diffusing light photography of fully developed isotropic ripple turbulence. Phys. Rev. Lett. 76, 4528–4531.Google Scholar
Yokoyama, N. 2004 Statistics of gravity waves obtained by direct numerical simulation. J. Fluid Mech. 501, 169–178.Google Scholar
Zakharov, V. E. 2010 Energy balance in a wind-driven sea. Phys. Scr. T 142, 014052.Google Scholar
Zakharov, V. E. & Filonenko, N. N. 1967a Energy spectrum for stochastic oscillations of the surface of a liquid. Sov. Phys. Dokl. 11, 881–883.Google Scholar
Zakharov, V. E. & Filonenko, N. N. 1967b Weak turbulence of capillary waves. J. Appl. Mech. Tech. Phys. 8, 37–40.Google Scholar
Zakharov, V. E., Korotkevich, A. O., Pushkarev, A. N. & Dyachenko, A. I. 2005 Mesoscopic wave turbulence. JETP Lett. 82, 487–491.Google Scholar
Zakharov, V. E., Korotkevich, A. O., Pushkarev, A. & Resio, D. 2007 Coexistence of weak and strong wave turbulence in a swell propagation. Phys. Rev. Lett. 99, 164501.Google Scholar
Zakharov, V. E., L’vov, V. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence. Springer.Google Scholar
Zakharov, V. E. & Zaslavsky, M. M. 1982 The kinetic equation and Kolmogorov spectra in the weak turbulence theory of wind waves. Izv. Atmos. Ocean. Phys. 18, 747–753.Google Scholar
Zhang, Q.-C. & Su, X. Y. 2002 An optical measurement of vortex shape at a free surface. Opt. Laser Technol. 34, 107–113.Google Scholar