Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-09T19:27:46.591Z Has data issue: false hasContentIssue false
  • English
  • Français

The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection

Published online by Cambridge University Press:  21 October 2011

Rudie P. J. Kunnen ,
Richard J. A. M. Stevens ,
Jim Overkamp ,
Chao Sun ,
GertJan F. van Heijst  and
Herman J. H. Clercx
Rudie P. J. Kunnen*
Affiliation:
Department of Physics and J.M. Burgers Centre for Fluid Dynamics, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
Richard J. A. M. Stevens
Affiliation:
Department of Science and Technology and J.M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Jim Overkamp
Affiliation:
Department of Physics and J.M. Burgers Centre for Fluid Dynamics, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
Chao Sun
Affiliation:
Department of Science and Technology and J.M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
GertJan F. van Heijst
Affiliation:
Department of Physics and J.M. Burgers Centre for Fluid Dynamics, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
Herman J. H. Clercx
Affiliation:
Department of Physics and J.M. Burgers Centre for Fluid Dynamics, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands Department of Applied Mathematics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When the classical Rayleigh–Bénard (RB) system is rotated about its vertical axis roughly three regimes can be identified. In regime I (weak rotation) the large-scale circulation (LSC) is the dominant feature of the flow. In regime II (moderate rotation) the LSC is replaced by vertically aligned vortices. Regime III (strong rotation) is characterized by suppression of the vertical velocity fluctuations. 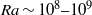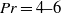Using results from experiments and direct numerical simulations of RB convection for a cell with a diameter-to-height aspect ratio equal to one at () and 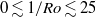we identified the characteristics of the azimuthal temperature profiles at the sidewall in the different regimes. In regime I the azimuthal wall temperature profile shows a cosine shape and a vertical temperature gradient due to plumes that travel with the LSC close to the sidewall. In regimes II and III this cosine profile disappears, but the vertical wall temperature gradient is still observed. It turns out that the vertical wall temperature gradient in regimes II and III has a different origin than that observed in regime I. It is caused by boundary layer dynamics characteristic for rotating flows, which drives a secondary flow that transports hot fluid up the sidewall in the lower part of the container and cold fluid downwards along the sidewall in the top part.

JFM classification

Boundary Layers: Boundary layer structure Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 688 , 10 December 2011 , pp. 422 - 442
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503.CrossRefGoogle Scholar
2. van Bokhoven, L. J. A. 2007 Experiments on rapidly rotating turbulent flows. PhD thesis, Eindhoven University of Technology.Google Scholar
3. Boubnov, B. M. & Golitsyn, G. S. 1986 Experimental study of convective structures in rotating fluids. J. Fluid Mech. 167, 503–531.CrossRefGoogle Scholar
4. Boubnov, B. M. & Golitsyn, G. S. 1990 Temperature and velocity field regimes of convective motions in a rotating plane fluid layer. J. Fluid Mech. 219, 215–239.CrossRefGoogle Scholar
5. Brown, E. & Ahlers, G. 2006a Effect of the Earth’s Coriolis force on turbulent Rayleigh–Bénard convection in the laboratory. Phys. Fluids 18, 125108–1–15.CrossRefGoogle Scholar
6. Brown, E. & Ahlers, G. 2006b Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
7. Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.CrossRefGoogle ScholarPubMed
8. Brown, E., Funfschilling, D., Nikolaenko, A. & Ahlers, G. 2005a Heat transport by turbulent Rayleigh–Bénard convection: effect of finite top and bottom conductivity. Phys. Fluids 17, 075108.CrossRefGoogle Scholar
9. Brown, E., Nikolaenko, A. & Ahlers, G. 2005b Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
10. Ecke, R. E. & Liu, Y. 1998 Traveling-wave and vortex states in rotating Rayleigh–Bénard convection. Intl J. Engng Sci. 36, 1471–1480.CrossRefGoogle Scholar
11. Fernando, H. J. S., Chen, R. & Boyer, D. L. 1991 Effects of rotation on convective turbulence. J. Fluid Mech. 228, 513–547.Google Scholar
12. Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
13. Greenspan, H. P & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.CrossRefGoogle Scholar
14. Hart, J. E., Kittelman, S. & Ohlsen, D. R. 2002 Mean flow precession and temperature probability density functions in turbulent rotating convection. Phys. Fluids 14, 955–962.CrossRefGoogle Scholar
15. Hart, J. E. & Olsen, D. R. 1999 On the thermal offset in turbulent rotating convection. Phys. Fluids 11, 2101–2107.CrossRefGoogle Scholar
16. van Heijst, G. J. F. 1983 The shear-layer structure in a rotating fluid near a differentially rotating sidewall. J. Fluid Mech. 130, 1–12.CrossRefGoogle Scholar
17. van Heijst, G. J. F. 1984 Source-sink flow in a rotating cylinder. J. Engng Maths 18, 247–257.CrossRefGoogle Scholar
18. van Heijst, G. J. F. 1986 Fluid flow in a partially-filled rotating cylinder. J. Engng Maths 20, 233–250.CrossRefGoogle Scholar
19. Homsy, G. M. & Hudson, J. L. 1969 Centrifugally driven thermal convection in a rotating cylinder. J. Fluid Mech. 35, 33–52.CrossRefGoogle Scholar
20. Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996a Hard turbulence in rotating Rayleigh–Bénard convection. Phys. Rev. E 53, R5557–R5560.CrossRefGoogle ScholarPubMed
21. Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996b Rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.CrossRefGoogle Scholar
22. Julien, K., Legg, S., McWilliams, J. & Werne, J. 1999 Plumes in rotating convection. Part 1. Ensemble statistics and dynamical balances. J. Fluid Mech. 391, 151–187.CrossRefGoogle Scholar
23. King, E. M., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. M. 2009 Boundary layer control of rotating convection systems. Nature 457, 301.CrossRefGoogle ScholarPubMed
24. Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2009 Turbulence statistics and energy budget in rotating Rayleigh–Bénard convection. Eur. J. Mech. (B/Fluids) 28, 578–589.CrossRefGoogle Scholar
25. Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2006 Heat flux intensification by vortical flow localization in rotating convection. Phys. Rev. E 74, 056306.CrossRefGoogle ScholarPubMed
26. Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008a Breakdown of large-scale circulation in turbulent rotating convection. Europhys. Lett. 84, 24001.CrossRefGoogle Scholar
27. Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008b Enhanced vertical inhomogeneity in turbulent rotating convection. Phys. Rev. Lett. 101, 174501.CrossRefGoogle ScholarPubMed
28. Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2010a Experimental and numerical investigation of turbulent convection in a rotating cylinder. J. Fluid Mech. 642, 445–476.CrossRefGoogle Scholar
29. Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2010b Vortex statistics in turbulent rotating convection. Phys. Rev. E 82, 036306.CrossRefGoogle ScholarPubMed
30. Legg, S., Julien, K., McWilliams, J. & Werne, J. 2001 Vertical transport by convection plumes: modification by rotation. Phys. Chem. Earth B 26, 259–262.CrossRefGoogle Scholar
31. Liu, Y. & Ecke, R. E. 1997 Heat transport scaling in turbulent Rayleigh–Bénard convection: effects of rotation and Prandtl number. Phys. Rev. Lett. 79, 2257–2260.CrossRefGoogle Scholar
32. Liu, Y. & Ecke, R. E. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80, 036314.CrossRefGoogle ScholarPubMed
33. Lohse, D. & Xia, K. Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
34. Moore, D. W. & Saffman, P. G. 1969 The shear-layer structure in a rotating fluid near a differentially rotating sidewall. Phil. Trans. R. Soc. A 264, 597–634.Google Scholar
35. Niemela, J. J., Babuin, S. & Sreenivasan, K. R. 2010 Turbulent rotating convection at high Rayleigh and Taylor numbers. J. Fluid Mech. 649, 509.CrossRefGoogle Scholar
36. Qiu, X. L. & Tong, P. 2001 Large scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.CrossRefGoogle ScholarPubMed
37. Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36, 309–335.CrossRefGoogle Scholar
38. Sakai, S. 1997 The horizontal scale of rotating convection in the geostrophic regime. J. Fluid Mech. 333, 85–95.CrossRefGoogle Scholar
39. Schmitz, S. & Tilgner, A. 2009 Heat transport in rotating convection without Ekman layers. Phys. Rev. E 80, 015305.CrossRefGoogle ScholarPubMed
40. Schmitz, S. & Tilgner, A. 2010 Transitions in turbulent rotating Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 104, 1029–0419.CrossRefGoogle Scholar
41. Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
42. Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010a Boundary layers in rotating weakly turbulent Rayleigh–Bénard convection. Phys. Fluids 22, 085103.CrossRefGoogle Scholar
43. Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2011 Effect of plumes on measuring the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 095110.Google Scholar
44. Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010c Optimal Prandtl number for heat transfer in rotating Rayleigh–Bénard convection. New J. Phys. 12, 075005.CrossRefGoogle Scholar
45. Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Ahlers, G. & Lohse, D. 2009 Transitions between turbulent states in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 024503.CrossRefGoogle ScholarPubMed
46. Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.CrossRefGoogle Scholar
47. Stewartson, K. 1966 On almost rigid rotations. Part 2. J. Fluid Mech. 26, 131–144.CrossRefGoogle Scholar
48. Verzicco, R. & Camussi, R. 1997 Transitional regimes of low-prandtl thermal convection in a cylindrical cell. Phys. Fluids 9, 1287–1295.CrossRefGoogle Scholar
49. Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
50. Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.CrossRefGoogle Scholar
51. Vorobieff, P. & Ecke, R. E. 2002 Turbulent rotating convection: an experimental study. J. Fluid Mech. 458, 191–218.CrossRefGoogle Scholar
52. Weiss, S., Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 224501.CrossRefGoogle ScholarPubMed
53. Zhong, F., Ecke, R. E. & Steinberg, V. 1993 Rotating Rayleigh–Bénard convection: asymmetrix modes and vortex states. J. Fluid Mech. 249, 135–159.CrossRefGoogle Scholar
54. Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.CrossRefGoogle Scholar
55. Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.CrossRefGoogle ScholarPubMed
56. Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
57. Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed