Article contents
The role of gravity in the prediction of the circular hydraulic jump radius for high-viscosity liquids
Published online by Cambridge University Press: 07 January 2019
Abstract
The free-surface flow formed by a circular jet impinging on a stationary disk is analysed theoretically. We develop a simple and coherent model to predict the location and height of the jump for high-viscosity liquids. The study explores the effect of gravity in the supercritical flow. The formulation reduces to a problem, involving only one parameter: 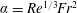 $\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$, where
$\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$, where 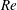 $Re$ and
$Re$ and 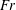 $Fr$ are the Reynolds and Froude numbers based on the flow rate and the jet radius. We show that the jump location coincides with the singularity in the thin-film equation when gravity is included, suggesting that the jump location can be determined without the knowledge of downstream flow conditions such as the jump height, the radius of the disk, which corroborates earlier observations in the case of type I circular hydraulic jumps. Consequently, there is no need for a boundary condition downstream to determine the jump radius. Our results corroborate well existing measurements and numerical simulation. Our predictions also confirm the constancy of the Froude number
$Fr$ are the Reynolds and Froude numbers based on the flow rate and the jet radius. We show that the jump location coincides with the singularity in the thin-film equation when gravity is included, suggesting that the jump location can be determined without the knowledge of downstream flow conditions such as the jump height, the radius of the disk, which corroborates earlier observations in the case of type I circular hydraulic jumps. Consequently, there is no need for a boundary condition downstream to determine the jump radius. Our results corroborate well existing measurements and numerical simulation. Our predictions also confirm the constancy of the Froude number 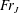 $Fr_{J}$ based on the jump radius and height as suggested by the measurements of Duchesne et al. (Europhys. Lett., vol. 107, 2014, 54002). We establish theoretically the conditions for
$Fr_{J}$ based on the jump radius and height as suggested by the measurements of Duchesne et al. (Europhys. Lett., vol. 107, 2014, 54002). We establish theoretically the conditions for 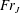 $Fr_{J}$ to remain independent of the flow rate. The subcritical flow and the height of the hydraulic jump are sought subject to the thickness at the edge of the disk, comprising contributions based on the capillary length and minimum flow energy. The thickness at the edge of the disk appears to be negligibly small for high-viscosity liquids.
$Fr_{J}$ to remain independent of the flow rate. The subcritical flow and the height of the hydraulic jump are sought subject to the thickness at the edge of the disk, comprising contributions based on the capillary length and minimum flow energy. The thickness at the edge of the disk appears to be negligibly small for high-viscosity liquids.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 20
- Cited by


