Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T14:36:43.497Z Has data issue: false hasContentIssue false
  • English
  • Français

The role of conservative forces in rotor aerodynamics

Published online by Cambridge University Press:  09 June 2014

G. A. M. van Kuik ,
D. Micallef ,
I. Herraez ,
A. H. van Zuijlen  and
D. Ragni
G. A. M. van Kuik*
Affiliation:
Faculty of Aerospace Engineering, Technical University Delft, Kluyverweg 1, 2629HS Delft, The Netherlands
D. Micallef
Affiliation:
Department of Mechanical Engineering, Faculty of Engineering, University of Malta, Msida MSD 2080, Malta
I. Herraez
Affiliation:
ForWind, Carl von Ossietzky Universität Oldenburg, Ammerländer Heerstrasse 136, 26129 Oldenburg, Germany
A. H. van Zuijlen
Affiliation:
Faculty of Aerospace Engineering, Technical University Delft, Kluyverweg 1, 2629HS Delft, The Netherlands
D. Ragni
Affiliation:
Faculty of Aerospace Engineering, Technical University Delft, Kluyverweg 1, 2629HS Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The theory to predict the performance and loads on rotors (propellers, screws, windmills) has a history of more than a century. Apart from modern computational fluid dynamics and vortex panel models taking the true blade geometry into account, most other models proceed from an infinitely thin actuator disc or line. These models assume an externally defined force field distributed at the disc or line, representing the loads on the real rotor. Given this force field, the flow is solved by momentum balances or by the equations of motion. The use of external force fields was discussed in textbooks of the first decades of the 20th century, but has received little attention since then. This paper investigates the higher-order effect of adding thickness to the actuator disc or changing the actuator line to a blade with cross-sectional dimensions. For the generation of a Rankine vortex by a force field acting on an actuator disc with thickness, an exact solution has been found in which not only the thrust and torque determine the flow, but also a radial force. This force is conservative, in contrast to the other force components. For rotor blades, a conservative normal and radial force acting on the chordwise bound vorticity is present. This explains the experimentally observed inboard motion of the tip vortex of model wind turbine rotors before the wake induction field drives it outboard. Simulations by computational fluid mechanics and a vortex panel code reproduce the inboard motion, but an actuator line analysis, in which the chordwise vorticity is absent, does not. The conservative load is only 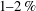$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1\mbox{--}2\, \%$ of the thrust on the entire blade but 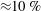${\approx }10\, \%$ of the thrust at the tip (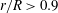$r/R>0.9$). Conservative forces at the disc and rotor blade vanish for vanishing disc thickness or blade cross-section, so play no role in any of the infinitely thin actuator disc or line methods. However, if higher-order effects of non-zero dimensions are to be modelled, the conservative force field has to be included.

JFM classification

Mathematical Foundations: General fluid mechanics Vortex Flows: Vortex interactions Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 750 , 10 July 2014 , pp. 284 - 315
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akay, B., Simão Ferreira, C. J., van Bussel, G. J. W. & Herraez, I.2012 Experimental and numerical quantification of radial flow in the root region of a HAWT. In Proceedings 50th AIAA Aerospace Sciences Meeting, Nashville, TN. AIAA Paper 2012-0896. Available at: http://repository.tudelft.nl/.Google Scholar
Batchelor, G. K. 1970 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Betz, A.1919 Schraubenpropeller mit geringstem Energieverlust. Dissertation. Göttinger Nachrichten. Göttingen.Google Scholar
Betz, A. 1920 Das Maximum der theoretisch möglichen Ausnützung des Windes durch Windmotoren. Z. Gesamte Turbinenwesen 26, 307–309.Google Scholar
Bragg, S. L. & Hawthorne, W. R. 1950 Some exact solutions of the flow through annual cascade actuator discs. J. Aeronaut. Sci. 17, 243–249.Google Scholar
Breslin, J. P. & Andersen, P. 1994 Hydrodynamics of Ship Propellers. Cambridge University Press.Google Scholar
Burton, T., Sharpe, D., Jenkins, N. & Bossanyi, E. 2001 The Wind Energy Handbook. John Wiley & Sons.CrossRefGoogle Scholar
del Campo, V., Ragni, D., Micallef, D., Diez, F. J. & Simao Ferreira, C.2013 3D Load estimation on a horizontal axis wind turbine using SPIV. Wind Energy (published online); doi:10.1002/we.1658.Google Scholar
Conway, J. T. 1995 Analytical solutions for the actuator disk with variable radial distribution of load. J. Fluid Mech. 297, 327–355.Google Scholar
Conway, J. T. 1998 Exact actuator disc solutions for non-uniform heavy loading and slipstream contraction. J. Fluid Mech. 365, 235–267.Google Scholar
Ferrer, E. & Munduate, X. 2007 Wind turbine blade tip comparison using CFD. J. Phys.: Conf. Ser. 75, 012005.Google Scholar
Froude, R. E. 1889 On the part played in propulsion by differences of fluid pressure. Trans. Inst. Nav. Archit. 30, 390–405.Google Scholar
Glauert, H. 1926 The Analysis of Experimental Results in the Windmill Brake and Vortex Ring States of an Airscrew. Aeronautical Research Committee, Reports and Memoranda, vol. 1026. H.M. Stationery Office.Google Scholar
Glauert, H. 1935 The general momentum theory. In Aerodynamic Theory (ed. W. F. Durand), Volume IV, Division L. Springer. (Reprinted 1963 Dover).Google Scholar
Goldstein, S. 1929 On the vortex theory of the screw propeller. Proc. R. Soc. Lond. A 123, 440–465.Google Scholar
Grey, R. B., McMahon, H. M., Shenoy, K. R. & Hanimer, M. L.1980 Surface pressure measurement at two tips of a model helicopter rotor in hover. NACA Tech. Rep. CR-3281.Google Scholar
Greenberg, M. D. 1972 Nonlinear actuator disc theory. Z. Flugwiss. 20 (3), 90–98.Google Scholar
Hand, M. M., Simms, D. A., Fingersh, L. J., Jager, D. W., Cotrell, J. R., Schreck, S. & Larwood, S. M.2001 Unsteady aerodynamics experiment phase VI: wind tunnel test configurations and available data campaigns. Tech Rep. NREL/TP-500-29955. National Renewable Energy Laboratory.Google Scholar
Herraez, I., Medjroubi, W., Stoevesandt, B. & Peinke, J. 2012 Aerodynamic simulation of the MEXICO rotor. In Proceedings of the Science of Making Torque from Wind, J. Phys.: Conf. Ser. (in press).Google Scholar
Horlock, J. H. 1978 Actuator Disk Theory. McGraw-Hill.Google Scholar
Joukowsky, N. E. 1912–1918 Four papers in vortex theory of screw propeller. In Théorie Tourbillonnaire de l’Hélice Propulsive, Gauthier-Villars, 1929, (French translation from Russian).Google Scholar
Joukowsky, N. E. 1918 Fourth paper in Transactions of the Office for Aerodynamic Calculations and Essays of the Superior Technical School of Moscow, 1918 (in Russian). Also published (in French) in Théorie Tourbillonnaire de l’Hélice Propulsive, Quatrième Mémoire. Gauthier-Villars, 1929.Google Scholar
Joukowsky, N. E. 1920 Windmill of the NEJ type. In Transactions of the Central Institute for Aero-Hydrodynamics of Moscow. Also published in: Collected Papers, Vol. VI. Joukowsky Institute for AeroHydrodynamics, 1937 (in Russian).Google Scholar
von Kármán, Th. & Burgers, J. M. 1935 Motion of a perfect fluid produced by external forces. In Aerodynamic Theory (ed. W. F. Durand), Volume II, Division E, chap. IIIA. Springer. (Reprinted 1963 Dover).Google Scholar
Katz, J. & Plotkin, A. 1991 Low-Speed Aerodynamics. McGraw-Hill.Google Scholar
Kűchemann, D. 1984 The Aerodynamic Design of Aircraft. Pergamon.Google Scholar
van Kuik, G. A. M.1991 On the limitations of Froude’s actuator disc concept. PhD thesis, Technical University Eindhoven, The Netherlands.Google Scholar
van Kuik, G. A. M. 2007 The Lanchester–Betz–Joukowsky limit. Wind Energy 10, 289–291.Google Scholar
van Kuik, G. A. M. 2012 The relationship between loads and power of a rotor and an actuator disc. In Proceedings of the Science of Making Torque from Wind, J. Phys.: Conf. Ser. (in press).Google Scholar
van Kuik, G. A. M.2014 On the generation of vorticity in rotor and disc flows. On the generation of vorticity by force fields in rotor and actuator flows. Renew. Energy (published online); http://dx.doi.org/10.1016/j.renene.2014.02.056.Google Scholar
van Kuik, G. A. M. & van Zuylen, A. H.2009 On actuator disc force fields generating wake vorticity. Abstracts of Euromech Symposium 508 on Wind Turbine Wakes, Madrid, pp. 26–28.Google Scholar
Kundu, P. K. 1990 Fluid Mechanics. Academic Press.Google Scholar
Lanchester, F. W. 1915 A contribution to the theory of propulsion and the screw propeller. Trans. Inst. Nav. Archit. 57, 98–116.Google Scholar
Leishman, J. G. 2000 Principles of Helicopter Aerodynamics. Cambridge University Press.Google Scholar
Lighthill, J. 1986 An Informal Introduction to Fluid Mechanics. Clarendon Press.Google Scholar
Madsen, H. A., Bak, C., Døssing, M., Mikkelsen, R. & Øye, S. 2010 Validation and modification of the blade element momentum theory based on comparisons with actuator disc simulations. Wind Energy 13, 373–389.Google Scholar
Manwell, J. F., McGowan, J. G. & Rogers, A. L. 2007 Wind Energy Explained. John Wiley & Sons.Google Scholar
Micallef, D.2012 3D flows near a HAWT rotor: a dissection of blade and wake contributions. PhD thesis, TU-Delft/University of Malta. Available at: http://repository.tudelft.nl/.Google Scholar
Micallef, D., Akay, B., Sant, T., Simão Ferreira, C. & van Bussel, G.2011 Experimental and numerical study of radial flow and its contribution to wake development of a HAWT. Proc. EWEA 2011 Conference, Brussels, 14–17 March. EWEA. Available at: http://www.ewea.org/annual2011/conference/conference-proceedings/.Google Scholar
Micallef, D., Akay, B., Simão Ferreira, C., Sant, T. & van Bussel, G. 2012 The origins of a wind turbine tip vortex. In Proceedings of the Science of Making Torque from Wind, J. Phys.: Conf. Ser. (in press).Google Scholar
Micallef, D., van Bussel, G., Simão Ferreira, C. & Sant, T. 2013 An investigation of radial velocities for a horizontal axis wind turbine in axial and yawed flows. Wind Energy 16, 529–544.Google Scholar
Mikkelsen, R., Øye, S., Sørensen, J. N., Madsen, H. A. & Shen, W. Z.2009 Analysis of wake expansion and induction near tip. Proc. EWEC09, Marseille, France. Available at: http://proceedings.ewea.org/ewec2009/proceedings/index.php?page=zip.Google Scholar
Milne-Thomson, L. M. 1966 Theoretical Aerodynamics. 4th edn Macmillan, (Reprinted 1973 Dover).Google Scholar
NREL 2013 Computer-aided engineering tools: SOWFA.http://wind.nrel.gov/designcodes/simulators/sowfa/ last visited January 2014.Google Scholar
Okulov, V. L. & Sørensen, J. N. 2010 Maximum efficiency of wind turbine rotors using Joukowsky and Betz approaches. J. Fluid Mech. 649, 497–508.Google Scholar
Okulov, V. L. & van Kuik, G. A. M. 2012 The Betz–Joukowsky limit: on the contribution to rotor aerodynamics by the British, German and Russian scientific schools. Wind Energy 15, 335–344.Google Scholar
OpenFOAM 2013 OpenFOAM: The open source CFD toolbox. www.openfoam.com last visited January 2014.Google Scholar
Øye, S.1990 A simple vortex model. Proceedings of 3rd IEA Symposium on the Aerodynamics of Wind Turbines, ETSU, Harwell, pp. 4.1–5.15.Google Scholar
Prandtl, L. 1918 Tragflügeltheorie I Mitteilung. Nachr. Ges. Wiss. Göttingen Math. Phys. Kl. 451–477.Google Scholar
Ragni, D., van Oudheusden, B. W. & Scarano, F. 2011 Non-intrusive aerodynamic loads analysis of an aircraft propeller blade. Exp. Fluids 51, 361–371.CrossRefGoogle Scholar
Ragni, D., van Oudheusden, B. W. & Scarano, F. 2012 3D pressure imaging of an aircraft propeller blade-tip flow by phase-locked stereoscopic PIV. Exp. Fluids 52, 463–477.Google Scholar
Rankine, W. J. M. 1865 On the mechanical principles of the action of propellers. Trans. Inst. Nav. Archit. 6, 13–39.Google Scholar
Réthoré, P., van der Laan, P., Troldborg, N., Zahle, F. & Sørensen, N. N. 2014 Verification and validation of an actuator disc model. Wind Energy 17, 919–937.Google Scholar
Roache, P. J. 1998 Verification and Validation in Computational Science and Engineering. Hermosa.Google Scholar
Rosen, A. & Gur, O. 2008 Novel approach to axisymmetric actuator disk modelling. AIAA J. 46, 2914–2925.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics, Cambridge Monographs on Mechanics and Applied Mathematics. Cambridge University Press.Google Scholar
Sanderse, B., van der Pijl, S. P. & Koren, B. 2011 Review of computational fluid dynamics for wind turbine wake aerodynamics. Wind Energy 14, 799–819.Google Scholar
Schepers, J. G., Boorsma, K. & Munduate, X. 2012 Final results from Mexnext-I: analysis of detailed aerodynamic measurements on a 4.5 m diameter rotor placed in the large German Dutch Wind Tunnel DNW. In Proceedings of the Science of Making Torque from Wind, J. Phys.: Conf. Ser. (in press).Google Scholar
Schepers, J. G. & Snel, H.2007 Model experiments in controlled conditions (MEXICO). ECN Report ECN-E-07–042.Google Scholar
Shen, W. Z., Mikkelsen, R., Sørensen, J. N. & Bak, C. 2005 Tip loss corrections for wind turbine computations. Wind Energy 8, 457–475.Google Scholar
Shen, W. Z., Zhu, W. J. & Sørensen, J. N. 2012 Actuator line/Navier–Stokes computations for the MEXICO rotor: comparison with detailed measurements. Wind Energy 15, 811–825.Google Scholar
Shives, M. & Crawford, C. 2013 Mesh and load distribution requirements for actuator line CFD simulations. Wind Energy 16, 1138–1196.CrossRefGoogle Scholar
Sibuet Watters, C. & Masson, C. 2010 Application of the actuator surface concept to wind turbine rotor aerodynamics. Wind Energy 13, 433–447.Google Scholar
Sørensen, J. N. & Shen, W. Z. 2002 Numerical modelling of wind turbine wakes. Trans. ASME: J. Fluids Engng 124, 393–399.Google Scholar
Sørensen, J. N., Shen, W. Z. & Munduate, X. 1998 Analysis of wake states by a full-field actuator disc model. Wind Energy 1, 73–88.Google Scholar
Sørensen, J. N. & van Kuik, G. A. M. 2011 General momentum theory for wind turbines at low tip speed ratios. Wind Energy 14, 821–839.Google Scholar
Spalart, P. R. 2003 On the simple actuator disc. J. Fluid Mech. 494, 399–405.Google Scholar
Spalart, P. R. & Allmaras, S. R. 1994 A one-equation turbulence model for aerodynamic flows. Rech. Aéronaut. 1 (1), 5–21.Google Scholar
Thwaites, B. 1960 Incompressible Aerodynamics. Clarendon Press.Google Scholar
Troldborg, N., Sørensen, J. N. & Mikkelsen, R. 2010 Numerical simulations of wake characteristics of a wind turbine in uniform inflow. Wind Energy 13, 86–99.Google Scholar
de Vries, O. 1979 Fluid Dynamic Aspects of Wind Energy Conversion, AGARDograph, vol. 243. AGARD.Google Scholar
Wald, Q. R. 2006 The aerodynamics of propellers. Prog. Aerosp. Sci. 42 (2), 85–128.Google Scholar
Wu, T. Y. 1962 Flow through a heavily loaded actuator disc. Schiffstechnik 9 (47), 134–138.Google Scholar
Xiao, J., Wu, J., Chen, L. & Shi, Z. 2011 Particle image velocimetry (PIV) measurements of tip vortex wake structure of wind turbine. Appl. Math. Mech. 32 (6), 729–738.Google Scholar