Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tom, Josin
and
Bragg, Andrew D.
2019.
Multiscale preferential sweeping of particles settling in turbulence.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
244.
Rodríguez-García, J. O.
and
Burguete, J.
2019.
Experimental lateral wall boundary layer behavior of a differentially rotating split-cylinder flow.
Physical Review E,
Vol. 99,
Issue. 2,
El-Sapa, Shreen
2019.
Settling slip velocity of a spherical particle in an unbounded micropolar fluid.
The European Physical Journal E,
Vol. 42,
Issue. 3,
Dey, Subhasish
Zeeshan Ali, Sk
and
Padhi, Ellora
2019.
Terminal fall velocity: the legacy of Stokes from the perspective of fluvial hydraulics.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 475,
Issue. 2228,
p.
20190277.
Lian, H.
Chang, X. Y.
and
Hardalupas, Y.
2019.
Time resolved measurements of droplet preferential concentration in homogeneous isotropic turbulence without mean flow.
Physics of Fluids,
Vol. 31,
Issue. 2,
Trang, Christ
Ahmed, Rahman
and
Kaosar, Mohammed Golam
2019.
Effect of density ratio on the dispersion of particles in a submerged liquid jet.
Computational Particle Mechanics,
Vol. 6,
Issue. 4,
p.
581.
Petersen, Alec J.
Baker, Lucia
and
Coletti, Filippo
2019.
Experimental study of inertial particles clustering and settling in homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 864,
Issue. ,
p.
925.
Clark, A
Machicoane, N
and
Aliseda, A
2019.
A quantitative study of track initialization of the four-frame best estimate algorithm for three-dimensional Lagrangian particle tracking.
Measurement Science and Technology,
Vol. 30,
Issue. 4,
p.
045302.
Wang, Y.
and
Lam, K.M.
2020.
Clustering behaviour and settling velocity of bidisperse inertial particles in turbulent open channel flow.
International Journal of Multiphase Flow,
Vol. 129,
Issue. ,
p.
103303.
Mora, Daniel Odens
Obligado, Martin
Aliseda, Alberto
and
Cartellier, Alain
2021.
Effect of
Reλ
and Rouse numbers on the settling of inertial droplets in homogeneous isotropic turbulence.
Physical Review Fluids,
Vol. 6,
Issue. 4,
Li, Cheng
Lim, Kaeul
Berk, Tim
Abraham, Aliza
Heisel, Michael
Guala, Michele
Coletti, Filippo
and
Hong, Jiarong
2021.
Settling and clustering of snow particles in atmospheric turbulence.
Journal of Fluid Mechanics,
Vol. 912,
Issue. ,
Mora, D. O.
Bourgoin, M.
Mininni, P. D.
and
Obligado, M.
2021.
Clustering of vector nulls in homogeneous isotropic turbulence.
Physical Review Fluids,
Vol. 6,
Issue. 2,
Berk, Tim
and
Coletti, Filippo
2021.
Dynamics of small heavy particles in homogeneous turbulence: a Lagrangian experimental study.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
De Souza, David
Zürner, Till
and
Monchaux, Romain
2021.
Simple distinction of similar-looking inertial particles and fluid tracers on camera images.
Experiments in Fluids,
Vol. 62,
Issue. 5,
Stafford, C. P.
and
Swailes, D. C.
2021.
Mass flux of dispersed particles in turbulence: Representations and the influence of correlation structure in gravitational settling.
Physical Review E,
Vol. 103,
Issue. 6,
Reartes, Christian
and
Mininni, Pablo D.
2021.
Settling and clustering of particles of moderate mass density in turbulence.
Physical Review Fluids,
Vol. 6,
Issue. 11,
Le Roy De Bonneville, F.
Zamansky, R.
Risso, F.
Boulin, A.
and
Haquet, J.-F.
2021.
Numerical simulations of the agitation generated by coarse-grained bubbles moving at large Reynolds number.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
Marchetti, Benjamin
Bergougnoux, Laurence
and
Guazzelli, Elisabeth
2021.
Falling clouds of particles in vortical flows.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Li, Cheng
Gao, Xi
Rowan, Steven L.
Hughes, Bryan
and
Rogers, William A.
2022.
Measuring binary fluidization of nonspherical and spherical particles using machine learning aided image processing.
AIChE Journal,
Vol. 68,
Issue. 7,
Brandt, Luca
and
Coletti, Filippo
2022.
Particle-Laden Turbulence: Progress and Perspectives.
Annual Review of Fluid Mechanics,
Vol. 54,
Issue. 1,
p.
159.
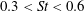 $0.3<St<0.6$
). Conditional averaging of the particle vertical velocity on the local concentration identifies three settling regimes: modest enhancement by single particle–turbulence interactions in low concentration regions, rapid settling velocity increases in clusters at intermediate concentrations and saturation of the settling enhancement at large concentrations. The latter effect, associated with four-way coupling, displays qualitative agreement with simulations in the literature and is a new experimental observation. Fluctuations up to an order of magnitude larger than the background volume fraction are measured using Voronoï analysis. A model is developed following a classic volume-averaged multiphase flow methodology to provide an interpretation of the three settling regimes and quantitative predictions consistent with the measurements.
$0.3<St<0.6$
). Conditional averaging of the particle vertical velocity on the local concentration identifies three settling regimes: modest enhancement by single particle–turbulence interactions in low concentration regions, rapid settling velocity increases in clusters at intermediate concentrations and saturation of the settling enhancement at large concentrations. The latter effect, associated with four-way coupling, displays qualitative agreement with simulations in the literature and is a new experimental observation. Fluctuations up to an order of magnitude larger than the background volume fraction are measured using Voronoï analysis. A model is developed following a classic volume-averaged multiphase flow methodology to provide an interpretation of the three settling regimes and quantitative predictions consistent with the measurements.


