Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T09:16:18.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Rivulet flow over a flexible beam

Published online by Cambridge University Press:  04 May 2016

P. D. Howell ,
H. Kim ,
M. G. Popova  and
H. A. Stone
P. D. Howell
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Oxford OX2 6GG, UK
H. Kim
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
M. G. Popova
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
H. A. Stone*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study theoretically and experimentally how a thin layer of liquid flows along a flexible beam. The flow is modelled using lubrication theory and the substrate is modelled as an elastica which deforms according to the Euler–Bernoulli equation. A constant flux of liquid is supplied at one end of the beam, which is clamped horizontally, while the other end of the beam is free. As the liquid film spreads, its weight causes the beam deflection to increase, which in turn enhances the spreading rate of the liquid. This feedback mechanism causes the front position 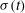${\it\sigma}(t)$ and the deflection angle at the front 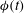${\it\phi}(t)$ to go through a number of different power-law behaviours. For early times, the liquid spreads like a horizontal gravity current, with ${\it\sigma}(t)\propto t^{4/5}$ and 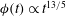${\it\phi}(t)\propto t^{13/5}$. For intermediate times, the deflection of the beam leads to rapid acceleration of the liquid layer, with ${\it\sigma}(t)\propto t^{4}$ and 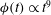${\it\phi}(t)\propto t^{9}$. Finally, when the beam has sagged to become almost vertical, the liquid film flows downward with 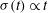${\it\sigma}(t)\propto t$ and 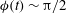${\it\phi}(t)\sim {\rm\pi}/2$. We demonstrate good agreement between these theoretical predictions and experimental results.

JFM classification

Interfacial Flows (free surface): Capillary flows Geophysical and Geological Flows: Gravity currents Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 796 , 10 June 2016 , pp. 285 - 305
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

P. D. Howell and H. Kim contributed equally to this work.

References

Crandall, S. H., Lardner, T. J., Archer, R. R., Cook, N. H. & Dahl, N. C. 1978 An Introduction to the Mechanics of Solids. McGraw-Hill.Google Scholar
Davis, R. H., Serayssol, J.-M. & Hinch, E. J. 1986 The elastohydrodynamic collision of two spheres. J. Fluid Mech. 163, 479–497.CrossRefGoogle Scholar
Dowson, D. & Ehret, P. 1999 Past, present and future studies in elastohydrodynamics. Proc. Inst. Mech. Engrs 213 (5), 317–333.Google Scholar
Duffy, B. R. & Moffatt, H. K. 1995 Flow of a viscous trickle on a slowly varying incline. Chem. Engng J. 60 (1–3), 141–146.Google Scholar
Duffy, B. R. & Moffatt, H. K. 1997 A similarity solution for viscous source flow on a vertical plane. Eur. J. Appl. Maths 8, 37–47.CrossRefGoogle Scholar
Flitton, J. C. & King, J. R. 2004 Moving-boundary and fixed-domain problems for a sixth-order thin-film equation. Eur. J. Appl. Maths 15 (06), 713–754.CrossRefGoogle Scholar
Fritz, J. A., Seminara, A., Roper, M., Pringle, A. & Brenner, M. P. 2013 A natural o-ring optimizes the dispersal of fungal spores. J. R. Soc. Interface 10 (85), 20130187.CrossRefGoogle ScholarPubMed
Gart, S., Mates, J. E., Megaridis, C. M. & Jung, S. 2015 Droplet impacting a cantilever: a leaf–raindrop system. Phys. Rev. Appl. 3 (4), 044019.CrossRefGoogle Scholar
Gilet, T. & Bourouiba, L. 2015 Fluid fragmentation shapes rain-induced foliar disease transmission. J. R. Soc. Interface 12 (104), 20141092.CrossRefGoogle ScholarPubMed
Gohar, R. 2001 Elastohydrodynamics. World Scientific.CrossRefGoogle Scholar
Hewitt, I. J., Balmforth, N. J. & De Bruyn, J. R. 2015 Elastic-plated gravity currents. Eur. J. Appl. Maths 26 (01), 1–31.CrossRefGoogle Scholar
Howell, P. D., Robinson, J. & Stone, H. A. 2013 Gravity-driven thin-film flow on a flexible substrate. J. Fluid Mech. 732, 190–213.CrossRefGoogle Scholar
Huppert, H. E. 1982a Flow and instability of a viscous current down a slope. Nature 300 (5891), 427–429.CrossRefGoogle Scholar
Huppert, H. E. 1982b The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.CrossRefGoogle Scholar
Leslie, G. A., Wilson, S. K. & Duffy, B. R. 2013 Three-dimensional coating and rimming flow: a ring of fluid on a rotating horizontal cylinder. J. Fluid Mech. 716, 51–82.CrossRefGoogle Scholar
Lister, J. R., Peng, G. G. & Neufeld, J. A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111 (15), 154501.CrossRefGoogle Scholar
Mow, V. C., Ratcliffe, A. & Poole, A. R. 1992 Cartilage and diarthrodial joints as paradigms for hierarchical materials and structures. Biomaterials 13 (2), 67–97.CrossRefGoogle ScholarPubMed
Pang, Y., Kim, H., Liu, Z. & Stone, H. A. 2014 A soft microchannel decreases polydispersity of droplet generation. Lab on a Chip 14 (20), 4029–4034.CrossRefGoogle ScholarPubMed
Paterson, C., Wilson, S. K. & Duffy, B. R. 2013 Pinning, de-pinning and re-pinning of a slowly varying rivulet. Eur. J. Mech. (B/Fluids) 41, 94–108.CrossRefGoogle Scholar
Salez, T. & Mahadevan, L. 2015 Elastohydrodynamics of a sliding, spinning and sedimenting cylinder near a soft wall. J. Fluid Mech. 779, 181–196.CrossRefGoogle Scholar
Sekimoto, K. & Leibler, L. 1993 A mechanism for shear thickening of polymer-bearing surfaces: elasto-hydrodynamic coupling. Europhys. Lett. 23 (2), 113–117.CrossRefGoogle Scholar
Shelley, M. J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43, 449–465.CrossRefGoogle Scholar
Skotheim, J. M. & Mahadevan, L. 2005 Soft lubrication: the elastohydrodynamics of nonconforming and conforming contacts. Phys. Fluids 17 (9), 092101.CrossRefGoogle Scholar
Tony, S. Y., Lauga, E. & Hosoi, A. E. 2006 Experimental investigations of elastic tail propulsion at low Reynolds number. Phys. Fluids 18 (9), 091701.Google Scholar
Wexler, J. S., Trinh, P. H., Berthet, H., Quennouz, N., du Roure, O., Huppert, H. E., Lindner, A. & Stone, H. A. 2013 Bending of elastic fibres in viscous flows: the influence of confinement. J. Fluid Mech. 720, 517–544.CrossRefGoogle Scholar
Wiggins, C. H., Riveline, D., Ott, A. & Goldstein, R. E. 1998 Trapping and wiggling: elastohydrodynamics of driven microfilaments. Biophys. J. 74 (2), 1043–1060.CrossRefGoogle ScholarPubMed
Wilson, S. K. & Duffy, B. R. 2005 Unidirectional flow of a thin rivulet on a vertical substrate subject to a prescribed uniform shear stress at its free surface. Phys. Fluids 17 (10), 108105.CrossRefGoogle Scholar
Zheng, Z., Griffiths, I. M. & Stone, H. A. 2015 Propagation of a viscous thin film over an elastic membrane. J. Fluid Mech. 784, 443–464.CrossRefGoogle Scholar

Howell et al. supplementary movie

A "small deflection" experiment

Download Howell et al. supplementary movie(Video)
Video 3.7 MB

Howell et al. supplementary movie

A "large deflection" experiment

Download Howell et al. supplementary movie(Video)
Video 1.4 MB