Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Myrtroeen, O. J.
and
Hunt, G. R.
2012.
On the transition from finite-volume negatively buoyant releases to continuous fountains.
Journal of Fluid Mechanics,
Vol. 698,
Issue. ,
p.
168.
Burridge, H. C.
and
Hunt, G. R.
2013.
The rhythm of fountains: the length and time scales of rise height fluctuations at low and high Froude numbers.
Journal of Fluid Mechanics,
Vol. 728,
Issue. ,
p.
91.
Srinarayana, N.
Armfield, S.W.
and
Lin, Wenxian
2013.
Behaviour of laminar plane fountains with a parabolic inlet velocity profile in a homogeneous fluid.
International Journal of Thermal Sciences,
Vol. 67,
Issue. ,
p.
87.
Richards, Tamar S.
Aubourg, Quentin
and
Sutherland, Bruce R.
2014.
Radial intrusions from turbulent plumes in uniform stratification.
Physics of Fluids,
Vol. 26,
Issue. 3,
Vinoth, B. R.
and
Panigrahi, P. K.
2014.
Characteristics of low Reynolds number non-Boussinesq fountains from non-circular sources.
Physics of Fluids,
Vol. 26,
Issue. 1,
Zhao, B.
Law, A. W. K.
Adams, E. E.
and
Er, J. W.
2014.
Formation of particle clouds.
Journal of Fluid Mechanics,
Vol. 746,
Issue. ,
p.
193.
Lin, Wen Xian
Liu, Tao
Gao, Wen Feng
and
Armfield, Steven W.
2014.
Three-Dimensional Direct Numerical Simulation of Unsteady Transitional Round Fountains in a Homogeneous Fluid.
Applied Mechanics and Materials,
Vol. 553,
Issue. ,
p.
150.
Burridge, H. C.
and
Hunt, G. R.
2014.
Scaling arguments for the fluxes in turbulent miscible fountains.
Journal of Fluid Mechanics,
Vol. 744,
Issue. ,
p.
273.
Mahmud, Hasan
Lin, Wenxian
Gao, Wenfeng
Armfield, S.W.
and
He, Yinghe
2015.
Behavior of the interaction between twin transitional round fountains in a homogeneous fluid, Part 2: Numerical study.
International Journal of Heat and Mass Transfer,
Vol. 86,
Issue. ,
p.
973.
Inam, Mohammad Ilias
Lin, Wenxian
Armfield, S.W.
and
He, Yinghe
2015.
Asymmetry and penetration of transitional plane fountains in stratified fluid.
International Journal of Heat and Mass Transfer,
Vol. 90,
Issue. ,
p.
1125.
Freire, Daniel
Kahan, Sandra
Cabeza, Cecilia
Sarasúa, Gustavo
and
Marti, Arturo C.
2015.
The formation of coherent structures within turbulent fountains in stratified media.
European Journal of Mechanics - B/Fluids,
Vol. 50,
Issue. ,
p.
89.
Frank, D.
and
Linden, P.F.
2015.
The effects of an opposing buoyancy force on the performance of an air curtain in the doorway of a building.
Energy and Buildings,
Vol. 96,
Issue. ,
p.
20.
Ezzamel, A.
Salizzoni, P.
and
Hunt, G. R.
2015.
Dynamical variability of axisymmetric buoyant plumes.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
p.
576.
Mehaddi, Rabah
Vauquelin, Olivier
and
Candelier, Fabien
2015.
Experimental non-Boussinesq fountains.
Journal of Fluid Mechanics,
Vol. 784,
Issue. ,
Hunt, G.R.
and
Burridge, H.C.
2015.
Fountains in Industry and Nature.
Annual Review of Fluid Mechanics,
Vol. 47,
Issue. 1,
p.
195.
Mahmud, Hasan
Lin, Wenxian
Gao, Wenfeng
Hill, Blair
Armfield, S.W.
and
He, Yinghe
2015.
Behavior of the interaction between twin transitional round fountains in a homogeneous fluid, Part 1: Experimental study.
International Journal of Heat and Mass Transfer,
Vol. 86,
Issue. ,
p.
957.
Burridge, H. C.
Mistry, A.
and
Hunt, G. R.
2015.
The effect of source Reynolds number on the rise height of a fountain.
Physics of Fluids,
Vol. 27,
Issue. 4,
Mingotti, Nicola
and
Woods, Andrew W.
2015.
On the transport of heavy particles through an upward displacement-ventilated space.
Journal of Fluid Mechanics,
Vol. 772,
Issue. ,
p.
478.
Mingotti, Nicola
and
Woods, Andrew W.
2015.
On the transport of heavy particles through a downward displacement-ventilated space.
Journal of Fluid Mechanics,
Vol. 774,
Issue. ,
p.
192.
Mehaddi, Rabah
Vaux, Samuel
Candelier, Fabien
and
Vauquelin, Olivier
2015.
On the modelling of steady turbulent fountains.
Environmental Fluid Mechanics,
Vol. 15,
Issue. 6,
p.
1115.
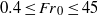 , into the dynamics, morphology and rise heights of Boussinesq turbulent axisymmetric fountains in quiescent uniform environments. Typically, these fountains are thought to rise to an initial height,
, into the dynamics, morphology and rise heights of Boussinesq turbulent axisymmetric fountains in quiescent uniform environments. Typically, these fountains are thought to rise to an initial height, 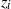 , before settling back and fluctuating about a lesser (quasi-) steady height,
, before settling back and fluctuating about a lesser (quasi-) steady height, 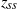 . Our measurements show that this is not always the case and the ratio of the fountain’s initial rise height to steady rise height,
. Our measurements show that this is not always the case and the ratio of the fountain’s initial rise height to steady rise height, 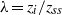 , varies widely,
, varies widely, 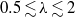 , across the range of
, across the range of 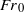 investigated. As a result of near-ideal start-up conditions provided by the experimental set-up we were consistently able to form a vortex at the fountain’s front. This enabled new insights into two features of the initial rise of turbulent fountains. Firstly, for
investigated. As a result of near-ideal start-up conditions provided by the experimental set-up we were consistently able to form a vortex at the fountain’s front. This enabled new insights into two features of the initial rise of turbulent fountains. Firstly, for  the initial rise height is less than the steady rise height. Secondly, for
the initial rise height is less than the steady rise height. Secondly, for 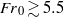 , the vortex formed at the fountain’s front pinches off, separates from the main body and rises high above the fountain; there is thus a third rise height to consider, namely, the maximum vortex rise height,
, the vortex formed at the fountain’s front pinches off, separates from the main body and rises high above the fountain; there is thus a third rise height to consider, namely, the maximum vortex rise height, 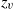 . From our observations we propose classifying turbulent axisymmetric fountains into five regimes (as opposed to the current three regimes) and present detailed descriptions of the flow in each. Finally, based on an analysis of the rise height fluctuations and the width of fountains in (quasi-) steady state we provide further insight into the physical cause of height fluctuations.
. From our observations we propose classifying turbulent axisymmetric fountains into five regimes (as opposed to the current three regimes) and present detailed descriptions of the flow in each. Finally, based on an analysis of the rise height fluctuations and the width of fountains in (quasi-) steady state we provide further insight into the physical cause of height fluctuations.