Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T15:21:52.144Z Has data issue: false hasContentIssue false
  • English
  • Français

Reynolds-number dependence of wall-pressure fluctuations in a pressure-induced turbulent separation bubble

Published online by Cambridge University Press:  07 November 2017

Hiroyuki Abe Open the ORCID record for Hiroyuki Abe [Opens in a new window]
Hiroyuki Abe*
Affiliation:
Japan Aerospace Exploration Agency, Tokyo 182-8522, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations are used to examine the behaviour of wall-pressure fluctuations 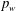$p_{w}$ in a flat-plate turbulent boundary layer with large adverse and favourable pressure gradients, involving separation and reattachment. The Reynolds number 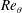$Re_{\unicode[STIX]{x1D703}}$ based on momentum thickness is equal to 300, 600 and 900. Particular attention is given to effects of Reynolds number on root-mean-square (r.m.s.) values, frequency/power spectra and instantaneous fields. The possible scaling laws are also examined as compared with the existing direct numerical simulation and experimental data. The r.m.s. value of 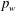$p_{w}$ normalized by the local maximum Reynolds shear stress 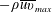$-\unicode[STIX]{x1D70C}\overline{uv}_{max}$ (Simpson et al. J. Fluid Mech. vol. 177, 1987, pp. 167–186; Na & Moin J. Fluid Mech. vol. 377, 1998b, pp. 347–373) leads to near plateau (i.e. 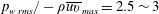$p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{uv}_{max}=2.5\sim 3$) in the adverse pressure gradient and separated regions in which the frequency spectra exhibit good collapse at low frequencies. The magnitude of 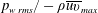$p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{uv}_{max}$ is however reduced down to 1.8 near reattachment where good collapse is also obtained with normalization by the local maximum wall-normal Reynolds stress 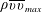$\unicode[STIX]{x1D70C}\overline{vv}_{max}$. Near reattachment, 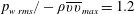$p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{vv}_{max}=1.2$ is attained unambiguously independently of the Reynolds number and pressure gradient. The present magnitude (1.2) is smaller than (1.35) obtained for step-induced separation by Ji & Wang (J. Fluid Mech. vol. 712, 2012, pp. 471–504). The reason for this difference is intrinsically associated with convective nature of a pressure-induced separation bubble near reattachment where the magnitude of 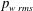$p_{w\,rms}$ depends essentially on the favourable pressure gradient. The resulting mean flow acceleration leads to delay of the r.m.s. peak after reattachment. Attention is also given to structures of 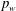$p_{w}$. It is shown that large-scale spanwise rollers of low pressure fluctuations are formed above the bubble, whilst changing to large-scale streamwise elongated structures after reattachment. These large-scale structures become more prominent with increasing 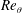$Re_{\unicode[STIX]{x1D703}}$ and affect 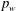$p_{w}$ significantly.

JFM classification

Boundary Layers: Boundary layer separation Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 563 - 598
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Matsuo, Y. 2004 Surface heat-flux fluctuations in a turbulent channel flow up to Re 𝜏 = 1020 with Pr = 0. 025 and 0. 71. Intl. J. Heat Fluid Flow 25, 404–419.Google Scholar
Abe, H., Mizobuchi, Y., Matsuo, Y. & Spalart, P. R. 2012 DNS and modeling of a turbulent boundary layer with separation and reattachment over a range of Reynolds numbers. Annual Research Briefs. pp. 311–322. Stanford University, Center for Turbulence Research.Google Scholar
Abe, H., Mizobuchi, Y., Matsuo, Y. & Spalart, P. R.2015 Direct numerical simulations of a turbulent separation bubble over a wide Reynolds-number range. 68th Annual Meeting of the APS Division of Fluid Dynamics, Boston, MA, November 22–24, 2015; Bull. Am. Phys. Soc. 60 (21), 360.Google Scholar
Alving, A. E. & Fernholz, H. H. 1996 Turbulence measurements around a mild separation bubble and downstream of reattachment. J. Fluid Mech. 322, 297–328.Google Scholar
Antonia, R. A., Teitel, M., Kim, J. & Browne, L. W. B. 1992 Low-Reynolds-number effects in a fully developed turbulent channel flow. J. Fluid Mech. 236, 579–605.Google Scholar
Blake, W. K. 1986 Mechanics of Flow-Induced Sound and Vibration I, II. Academic.Google Scholar
Bradshaw, P. 1967 ‘Inactive’ motion and pressure fluctuations in turbulent boundary layers. J. Fluid Mech. 30, 241–258.CrossRefGoogle Scholar
Bradshaw, P.1973 Effects of streamline curvature on turbulent flow. AGARDograph 169. AGARD.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Cheng, W., Pullin, D. I. & Samtaney, R. 2015 Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer. J. Fluid Mech. 785, 78–108.Google Scholar
Choi, H. & Moin, P. 1990 On the space-time characteristics of wall pressure fluctuations. Phys. Fluids A2 (8), 1450–1460.Google Scholar
Driver, D. M., Seegmiller, H. L. & Marvin, J. G. 1987 Time-dependent behavior of a reattaching shear layer. AIAA J. 25 (7), 914–919.Google Scholar
Durbin, P. A. 1991 Near-wall turbulence closure modeling without ‘damping functions’. Theor. Comput. Fluid Dyn. 3, 1–13.Google Scholar
Eaton, J. K. & Johnston, J. P. 1981 A review of research on subsonic turbulent flow reattachment. AIAA J. 19 (9), 1093–1100.Google Scholar
Farabee, T. M. & Casarella, M. J. 1986 Measurements of fluctuating wall pressure for separated/reattached boundary layer flows. Trans. ASME J. Vib., Acoust. Stress, Reliab. Design 106, 343–350.Google Scholar
George, W. K., Beuther, P. D. & Arndt, R. E. 1984 Pressure spectra in turbulent free shear flows. J. Fluid Mech. 148, 155–191.Google Scholar
Imamura, T., Enomoto, S., Yokokawa, Y. & Yamamoto, K. 2008 Three-dimensional unsteady flow computations around a conventional slat of high-lift devices. AIAA J. 46 (5), 1045–1053.Google Scholar
Ji, M. & Wang, M. 2012 Surface pressure fluctuations on steps immersed in turbulent boundary layers. J. Fluid Mech. 712, 471–504.Google Scholar
Jones, B. G., Adrian, R. J., Nithianandan, C. K. & Planchon, H. P. 1979 Spectra of turbulent static pressure fluctuations in jet mixing layers. AIAA J. 17 (5), 449–457.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kiya, M. & Sasaki, K. 1983 Structure of a turbulent separation bubble. J. Fluid Mech. 137, 83–113.Google Scholar
Krogstad, P.-Å & Skåre, P. E. 1995 Influence of a strong adverse pressure gradient on the turbulent structure in a boundary layer. Phys. Fluids 7 (8), 2014–2024.Google Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.Google Scholar
Lee, J-H. & Sung, H. J. 2008 Effects of an adverse pressure gradient on a turbulent boundary layer. Intl. J. Heat Fluid Flow 29, 568–578.Google Scholar
Lee, J-H. & Sung, H. J. 2009 Structures in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 639, 101–131.Google Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulation. J. Comp. Phys. 140, 233–258.CrossRefGoogle Scholar
Mabey, D. G. 1972 Analysis and correlation of data on pressure fluctuations in separated flow. J. Aircraft 9 (9), 642–645.Google Scholar
Mabey, D. G. 1982 Comment on ‘a review of research on subsonic turbulent flow attachment’. AIAA J. 20 (11), 1632.CrossRefGoogle Scholar
Manhart, M. & Friedrich, R. 2002 DNS of a turbulent boundary layer with separation. Intl J. Heat Fluid Flow 23 (5), 572–581.Google Scholar
Mohammed-Taifour, A. & Weiss, J. 2016 Unsteadiness in a large turbulent separation bubble. J. Fluid Mech. 799, 383–412.Google Scholar
Monty, J., Harun, Z. & Marusic, I. 2011 A parametric study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32, 575–585.CrossRefGoogle Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comp. Phys. 143, 90–124.CrossRefGoogle Scholar
Na, Y. & Moin, P. 1998a Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.Google Scholar
Na, Y. & Moin, P. 1998b The structure of wall-pressure fluctuations in turbulent boundary layers with adverse pressure gradient and separation. J. Fluid Mech. 377, 347–373.Google Scholar
Panton, R. L. & Lineberger, J. H. 1974 Wall pressure spectra calculations for equilibrium boundary layers. J. Fluid Mech. 65, 261–287.Google Scholar
Patrick, W. P.1987 Flowfield measurements in a separated and reattached flat plate turbulent boundary layer. NASA Tech. Rep. 4052.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6, 903–923.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comp. Phys. 228, 4218–4231.Google Scholar
Simpson, R. L., Chew, Y.-T. & Shivaprasad, B. G. 1981 The structure of a separating turbulent boundary layer. Part 1. Mean flow and Reynolds stresses. J. Fluid Mech. 113, 23–51.Google Scholar
Simpson, R. L., Ghodbane, M. & Mcgrath, B. E. 1987 Surface pressure fluctuations in a separating turbulent boundary layer. J. Fluid Mech. 177, 167–186.Google Scholar
Skote, M. & Henningson, D. 2002 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 471, 107–136.Google Scholar
Song, S. & Eaton, J. K. 2004 Reynolds number effects on a turbulent boundary layer with separation, reattachment, and recovery. Exp. Fluids 36, 246–258.CrossRefGoogle Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to R 𝜃 = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Spalart, P. R., Strelets, M. & Travin, A. 2006 Direct numerical simulation of large-eddy-break-up devices in a boundary layer. Intl J. Heat Fluid Flow 27, 902–910.Google Scholar
Spalart, P. R. & Coleman, G. N. 1997 Numerical study of a separation bubble with heat transfer. Eur. J. Mech. (B/Fluids) 16, 169–189.Google Scholar
Thacker, A., Auburn, S., Leroy, A. & Devinant, P. 2013 Experimental characterization of flow unsteadiness in the centreline plane of an ahmed body near slant. Exp. Fluids 54, 1479.Google Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23, 79–107.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11, 97–120.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Troutt, T. R., Scheelke, B. & Norman, T. R. 1984 Organized structures in a reattaching separated flow field. J. Fluid Mech. 143, 413–427.Google Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.Google Scholar
Weiss, J., Mohammed-Taifour, A. & Schwaab, Q. 2015 Unsteady behavior of a pressure-induced turbulent separation bubble. AIAA J. 53 (9), 2634–2645.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally-zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.Google Scholar