Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-20T00:14:59.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Revisiting the subgrid-scale Prandtl number for large-eddy simulation

Published online by Cambridge University Press:  03 August 2016

Dan Li
Dan Li*
Affiliation:
Department of Earth and Environment, Boston University, Boston, MA 02215, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The subgrid-scale (SGS) Prandtl number (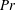$Pr$) is an important parameter in large-eddy simulation. Prior models often assume that the ‘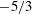$-5/3$’ inertial subrange scaling applies to the wavenumber range from 0 to 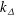$k_{\unicode[STIX]{x1D6E5}}$ (the wavenumber corresponding to the filter scale 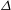$\unicode[STIX]{x1D6E5}$) and yield a 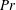$Pr$ that is stability-independent and scale-invariant, which is inconsistent with experimental data and the results of dynamic models. In this study, the SGS Prandtl number is revisited by solving the co-spectral budgets of momentum and heat fluxes in an idealized but thermally stratified atmospheric surface layer. The SGS Prandtl number from the co-spectral budget model shows a strong dependence on the atmospheric stability and increases (decreases) as the atmosphere becomes stable (unstable), which is in good agreement with recent field experimental data. The dependence of 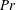$Pr$ on the filter scale is also captured by the co-spectral budget model: as the filter scale becomes smaller, the SGS Prandtl number decreases. Finally, the value of SGS Prandtl number under neutral conditions is shown to be caused by the dissimilarity between momentum and heat in the pressure decorrelation term and the flux transfer term. When the dissimilarity exists only in the flux transfer term, the fact that under neutral conditions the SGS Prandtl number is usually smaller than the turbulent Prandtl number for Reynolds-averaged Navier–Stokes simulations is an indication of a stronger spectral transfer coefficient for heat than for momentum. The model proposed in this study can be readily implemented.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence modelling
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , R2
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Basu, S. & Porté-Agel, F. 2006 Large-eddy simulation of stably stratified atmospheric boundary layer turbulence: a scale-dependent dynamic modeling approach. J. Atmos. Sci. 63, 2074–2091.CrossRefGoogle Scholar
Bos, W. J. T. & Bertoglio, J. P. 2007 Inertial range scaling of scalar flux spectra in uniformly sheared turbulence. Phys. Fluids 19, 025104.CrossRefGoogle Scholar
Bos, W. J. T., Touil, H. & Bertoglio, J. P. 2005 Reynolds number dependency of the scalar flux spectrum in isotropic turbulence with a uniform scalar gradient. Phys. Fluids 17 (12), 125108.CrossRefGoogle Scholar
Bos, W. J. T., Touil, H., Shao, L. & Bertogli, J. P. 2004 On the behavior of the velocity–scalar cross correlation spectrum in the inertial range. Phys. Fluids 16, 3818–3823.CrossRefGoogle Scholar
Bou-Zeid, E., Higgins, C., Huwald, H., Parlange, M. B. & Meneveau, C. 2010 Field study of the dynamics and modelling of subgrid scale turbulence in a stable atmospheric surface layer over a glacier. J. Fluid Mech. 665, 480–515.CrossRefGoogle Scholar
Bou-Zeid, E., Vercauteren, N., Parlange, M. B. & Meneveau, C. 2008 Scale dependence of subgrid-scale model coefficients: an a priori study. Phys. Fluids 20 (11), 115106.CrossRefGoogle Scholar
Brown, A. R., Derbyshire, S. H. & Mason, P. J. 1994 Large-eddy simulation of stable atmospheric boundary layers with a revised stochastic subgrid model. Q. J. R. Meterol. Soc. 120 (520), 1485–1512.Google Scholar
Businger, J. A., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28 (2), 181–191.2.0.CO;2>CrossRefGoogle Scholar
Calaf, M., Parlange, M. B. & Meneveau, C. 2011 Large eddy simulation study of scalar transport in fully developed wind-turbine array boundary layers. Phys. Fluids 23 (12), 126603.CrossRefGoogle Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22 (4), 469–473.CrossRefGoogle Scholar
Deardorff, J. W. 1973 The use of subgrid transport equations in a three-dimensional model of atmospheric turbulence. Trans. ASME J. Fluids Engng 95 (3), 429–438.CrossRefGoogle Scholar
Deardorff, J. W. 1980 Stratocumulus-capped mixed layers derived from a three-dimensional model. Boundary-Layer Meteorol. 18 (4), 495–527.CrossRefGoogle Scholar
Högström, U. L. F. 1988 Non-dimensional wind and temperature profiles in the atmospheric surface layer: a re-evaluation. In Topics in Micrometeorology. A Festschrift for Arch Dyer, pp. 55–78. Springer.CrossRefGoogle Scholar
Kaimal, J. C. & Finnigan, J. C. 1994 Atmospheric Boundary Layer Flows: Their Structure and Measurement. Oxford University Press.CrossRefGoogle Scholar
Katul, G. G., Li, D., Chamecki, M. & Bou-Zeid, E. 2013 Mean scalar concentration profile in a sheared and thermally stratified atmospheric surface layer. Phys. Rev. E 87 (2), 023004.Google Scholar
Katul, G. G., Porporato, A., Shah, S. & Bou-Zeid, E. 2014 Two phenomenological constants explain similarity laws in stably stratified turbulence. Phys. Rev. E 89 (2), 023007.Google ScholarPubMed
Kolmogorov, A. N. 1941 The local structure of turbulence in an incompressible fluid at very high Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Li, D. & Bou-Zeid, E. 2011 Coherent structures and the dissimilarity of turbulent transport of momentum and scalars in the unstable atmospheric surface layer. Boundary-Layer Meteorol. 140 (2), 243–262.CrossRefGoogle Scholar
Li, D., Katul, G. G. & Bou-Zeid, E. 2012 Mean velocity and temperature profiles in a sheared diabatic turbulent boundary layer. Phys. Fluids 24 (10), 105105.CrossRefGoogle Scholar
Li, D., Katul, G. G. & Bou-Zeid, E. 2015a Turbulent energy spectra and cospectra of momentum and heat fluxes in the stable atmospheric surface layer. Boundary-Layer Meteorol. 157 (1), 1–21.CrossRefGoogle Scholar
Li, D., Katul, G. G. & Zilitinkevich, S. S. 2015b Revisiting the turbulent Prandtl number in an idealized atmospheric surface layer. J. Atmos. Sci. 72 (6), 2394–2410.CrossRefGoogle Scholar
Li, D., Salesky, S. T. & Banerjee, T. 2016 Connections between the Ozmidov scale and mean velocity profile in stably stratified atmospheric surface layers. J. Fluid Mech. 797, R3.CrossRefGoogle Scholar
Lilly, D. K. 1967 The representation of small scale turbulence in numerical simulation experiments. In IBM Scientific Computing Symposium on Environmental Sciences, pp. 195–210. White Plains.Google Scholar
Lumley, J. L. 1964 The spectrum of nearly inertial turbulence in a stably stratified fluid. J. Atmos. Sci. 21 (1), 99–102.2.0.CO;2>CrossRefGoogle Scholar
Mason, P. J. 1989 Large-eddy simulation of the convective atmospheric boundary layer. J. Atmos. Sci. 46 (11), 1492–1516.2.0.CO;2>CrossRefGoogle Scholar
Mason, P. J. & Brown, A. R. 1999 On subgrid models and filter operations in large eddy simulations. J. Atmos. Sci. 56 (13), 2101–2114.2.0.CO;2>CrossRefGoogle Scholar
Moeng, C. H. & Wyngaard, J. C. 1988 Spectral analysis of large-eddy simulations of the convective boundary layer. J. Atmos. Sci. 45 (23), 3573–3587.2.0.CO;2>CrossRefGoogle Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the ground layer of the atmosphere. Akad. Nauk. SSSR. Geofiz. Inst. Trudy 151, 163–187.Google Scholar
Obukhov, A. M. 1949 Structure of the temperature field in a turbulent flow. Izv. Akad. Nauk SSSR Ser. Geogr. Geophys 13, 58–69.Google Scholar
Panchev, S. 1971 Random Functions and Turbulence. Pergamon.Google Scholar
Pitsch, H. & Steiner, H. 2000 Large-eddy simulation of a turbulent piloted methane/air diffusion flame (Sandia flame D). Phys. Fluids 12 (10), 2541–2554.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Porté-Agel, F. 2004 A scale-dependent dynamic model for scalar transport in large-eddy simulations of the atmospheric boundary layer. Boundary-Layer Meteorol. 112 (1), 81–105.CrossRefGoogle Scholar
Porté-Agel, F., Parlange, M. B., Meneveau, C. & Eichinger, W. E. 2001 A priori field study of the subgrid-scale heat fluxes and dissipation in the atmospheric surface layer. J. Atmos. Sci. 58 (18), 2673–2698.2.0.CO;2>CrossRefGoogle Scholar
Saddoughi, S. & Veeravalli, S. 1994 Local isotropy in turbulent boundary layers at high Reynolds number flow. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Schumann, U. 1991 Subgrid length-scales for large-eddy simulation of stratified turbulence. Theor. Comput. Fluid Dyn. 2 (5–6), 279–290.CrossRefGoogle Scholar
Schumann, U., Grötzbach, G. & Kleiser, L. 1980 Direct numerical simulation of turbulence. In Prediction Methods for Turbulent Flows (ed. Kollmann, W.), vol. 1, pp. 123–258. Hemisphere.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.2.3.CO;2>CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (11), 2778–2784.CrossRefGoogle Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the Obukhov–Corrsin constant. Phys. Fluids 8 (1), 189–196.CrossRefGoogle Scholar
Stoll, R. & Porté-Agel, F. 2006 Dynamic subgrid-scale models for momentum and scalar fluxes in large-eddy simulations of neutrally stratified atmospheric boundary layers over heterogeneous terrain. Water Resour. Res. 42 (1), W01409.CrossRefGoogle Scholar
Stoll, R. & Porté-Agel, F. 2008 Large-eddy simulation of the stable atmospheric boundary layer using dynamic models with different averaging schemes. Boundary-Layer Meteorol. 126 (1), 1–28.CrossRefGoogle Scholar
Stull, R. B. 1988 An Introduction to Boundary Layer Meteorology. Kluwer Academic.CrossRefGoogle Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 132, 476–490.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Vercauteren, N., Bou-Zeid, E., Parlange, M. B., Lemmin, U., Huwald, H., Selker, J. & Meneveau, C. 2008 Subgrid-scale dynamics for water vapor, heat, and momentum over a lake. Boundary-Layer Meteorol. 128 (2), 205–228.CrossRefGoogle Scholar