Hostname: page-component-7b9c58cd5d-nzzs5 Total loading time: 0 Render date: 2025-03-15T13:11:47.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Resonance of the thermal boundary layer adjacent to an isothermally heated vertical surface

Published online by Cambridge University Press:  29 April 2013

Yongling Zhao ,
Chengwang Lei  and
John C. Patterson
Yongling Zhao*
Affiliation:
School of Civil Engineering, The University of Sydney, Sydney, NSW 2006, Australia
Chengwang Lei
Affiliation:
School of Civil Engineering, The University of Sydney, Sydney, NSW 2006, Australia
John C. Patterson
Affiliation:
School of Civil Engineering, The University of Sydney, Sydney, NSW 2006, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The instability characteristics and resonance of a natural convection boundary layer adjacent to an isothermally heated vertical surface are investigated using direct stability analyses. The detailed streamwise evolution of the boundary-layer frequencies is visualized via the power spectra of the temperature time series in the thermal boundary layer. It is found that the entire thermal boundary layer may be divided into three distinct regions according to the frequency profile, which include an upstream low-frequency region, a transitional region (with both low- and high-frequency bands) and a downstream high-frequency region. The high-frequency band in the downstream region determines the resonance characteristics of the thermal boundary layer, which can be triggered by a single-mode perturbation at frequencies within the high-frequency band. The single-mode perturbation experiments further reveal that the maximum resonance of the thermal boundary layer is triggered by a perturbation at the characteristic frequency of the boundary layer. 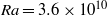For the boundary-layer flow at $\mathit{Ra}= 3. 6\times 1{0}^{10} $ and 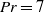$\mathit{Pr}= 7$, a net heat transfer enhancement of up to 44 % is achieved by triggering resonance of the boundary layer. This significant enhancement of heat transfer is due to the resonance-induced advancement of the laminar–turbulent transition, which is found to be dependent on the perturbation frequency and amplitude. Evidence from different perspectives revealing the same position of the transition are provided and discussed. The outcomes of this investigation demonstrate the prospect of a resonance-based approach for enhancing heat transfer.

JFM classification

Convection: Buoyant boundary layers Convection: Convection Flow Control: Instability control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 305 - 336
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aberra, T., Armfield, S., Behnia, M. & McBain, G. D. 2006 Stability of natural convection boundary layer flow on an evenly heated vertical plate. Am. Inst. Phys. Conf. Proc. 832, 456–460.Google Scholar
Aberra, T., Armfield, S. W., Behnia, M. & McBain, G. D. 2012 Boundary layer instability of the natural convection flow on a uniformly heated vertical plate. Intl J. Heat Mass Transfer 55 (21–22), 6097–6108.CrossRefGoogle Scholar
Antohe, B. V. & Lage, J. L. 1996 Amplitude effect on convection induced by time-periodic horizontal heating. Intl J. Heat Mass Transfer 39 (6), 1121–1133.CrossRefGoogle Scholar
Armfield, S. & Janssen, R. 1996 A direct boundary-layer stability analysis of steady-state cavity convection flow. Intl J. Heat Fluid Flow 17 (6), 539–546.CrossRefGoogle Scholar
Armfield, S. W. & Patterson, J. C. 1992 Wave properties of natural-convection boundary layers. J. Fluid Mech. 239, 195–211.CrossRefGoogle Scholar
Brooker, A. M. H., Patterson, J. C., Graham, T. & Schöpf, W. 2000 Convective instability in a time-dependent buoyancy driven boundary layer. Intl J. Heat Mass Transfer 43 (2), 297–310.CrossRefGoogle Scholar
Dring, R. P. & Gebhart, B. 1968 A theoretical investigation of disturbance amplification in external laminar natural convection. J. Fluid Mech. 34 (3), 551–564.CrossRefGoogle Scholar
Eckert, E. R. G. & Soehnghen, E. 1951 Interferometric studies on the stability and transition to turbulence of a free-convection boundary layer. Proc. Gen. Disc. Heat Transfer, Proc. Meet. London, p. 321–323. IME and ASME.Google Scholar
Gebhart, B. 1973 Instability, transition, and turbulence in buoyancy-induced flows. Annu. Rev. Fluid Mech. 5 (1), 213–246.CrossRefGoogle Scholar
Gebhart, B. & Mahajan, R. 1975 Characteristic disturbance frequency in vertical natural convection flow. Intl J. Heat Mass Transfer 18 (10), 1143–1148.CrossRefGoogle Scholar
Holman, J. P., Gartrell, H. E. & Soehnghen, E. E. 1960 An interferometric method of studying boundary layer oscillations. J. Heat Transfer 82 (3), 263–264.CrossRefGoogle Scholar
Janssen, R. & Armfield, S. 1996 Stability properties of the vertical boundary layers in differentially heated cavities. Intl J. Heat Fluid Flow 17 (6), 547–556.CrossRefGoogle Scholar
Janssen, R. J. A. & Henkes, R. A. W. M. 1995 Influence of Prandtl number on instability mechanisms and transition in a differentially heated square cavity. J. Fluid Mech. 290, 319–344.CrossRefGoogle Scholar
Kim, S. K., Kim, S. Y. & Choi, Y. D. 2002 Resonance of natural convection in a side heated enclosure with a mechanically oscillating bottom wall. Intl J. Heat Mass Transfer 45 (15), 3155–3162.CrossRefGoogle Scholar
Kim, S. K., Kim, S. Y. & Choi, Y. D. 2005 Amplification of boundary layer instability by hot wall thermal oscillation in a side heated cavity. Phys. Fluids 17 (1), 014103.CrossRefGoogle Scholar
Knowles, C. P. & Gebhart, B. 1968 The stability of the laminar natural convection boundary layer. J. Fluid Mech. 34 (4), 657–686.CrossRefGoogle Scholar
Kwak, H. S. & Hyun, J. M. 1996 Natural convection in an enclosure having a vertical sidewall with time-varying temperature. J. Fluid Mech. 329, 65–88.CrossRefGoogle Scholar
Kwak, H. S., Kuwahara, K. & Hyun, J. M. 1998 Resonant enhancement of natural convection heat transfer in a square enclosure. Intl J. Heat Mass Transfer 41 (18), 2837–2846.CrossRefGoogle Scholar
Lage, J. L. & Bejan, A. 1993 The resonance of natural convection in an enclosure heated periodically from the side. Intl J. Heat Mass Transfer 36 (8), 2027–2038.CrossRefGoogle Scholar
Lei, C. & Patterson, J. C. 2003 A direct stability analysis of a radiation-induced natural convection boundary layer in a shallow wedge. J. Fluid Mech. 480, 161–184.CrossRefGoogle Scholar
Leonard, B. P. 1979 A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Meth. Appl. Engng 19 (1), 59–98.CrossRefGoogle Scholar
Lin, W., Armfield, S. W. & Patterson, J. C. 2008 Unsteady natural convection boundary-layer flow of a linearly-stratified fluid with an evenly heated semi-infinite vertical plate. Intl J. Heat Mass Transfer 51 (1–2), 327–343.CrossRefGoogle Scholar
McBain, G. D., Armfield, S. W. & Desrayaud, G. 2007 Instability of the buoyancy layer on an evenly heated vertical wall. J. Fluid Mech. 587, 453–469.CrossRefGoogle Scholar
Nachtsheim, P. R. 1963 Stability of free convection boundary-layer flows, NASA Tech. Note D-2089.Google Scholar
Paolucci, S. & Chenoweth, D. R. 1989 Transition to chaos in a differentially heated vertical cavity. J. Fluid. Mech. 201, 379–410.CrossRefGoogle Scholar
Patankar, S. V. 1980 Numerical Heat Transfer and Fluid Flow. Hemisphere.Google Scholar
Patterson, J. C., Graham, T., Schöpf, W. & Armfield, S. W. 2002 Boundary layer development on a semi-infinite suddenly heated vertical plate. J. Fluid Mech. 453, 39–55.CrossRefGoogle Scholar
Patterson, J. C. & Imberger, J. 1980 Unsteady natural convection in a rectangular cavity. J. Fluid Mech. 100 (1), 65–86.CrossRefGoogle Scholar
Paul, M. C. & Rees, D. A. S. 2008 Numerical investigation of the linear stability of a free convection boundary layer flow using a thermal disturbance with a slowly increasing frequency. J. Heat Transfer 130 (12), 122501.CrossRefGoogle Scholar
Paul, M. C., Rees, D. A. S. & Wilson, M. 2008 Thermal receptivity of free convective flow from a heated vertical surface: linear waves. Intl J. Therm. Sci. 47 (10), 1382–1392.CrossRefGoogle Scholar
Paul, M. C., Rees, D. A. S. & Wilson, M. 2010 Thermal receptivity of free convective flow from a heated vertical surface: nonlinear waves. Comput. Therm. Sci. 2 (5), 421–437.CrossRefGoogle Scholar
Plapp, J. P. 1957 The analytic study of laminar boundary layer stability in free convection. J. Aero. Sci. 24, 318–319.Google Scholar
Polymeropoulos, C. E. & Gebhart, B. 1967 Incipient instability in free convection laminar boundary layers. J. Fluid Mech. 30 (2), 225–239.CrossRefGoogle Scholar
Qureshi, Z. H. & Gebhart, B. 1978 Transition and transport in a buoyancy driven flow in water adjacent to a vertical uniform flux surface. Intl J. Heat Mass Transfer 21 (12), 1467–1479.CrossRefGoogle Scholar
Szewczyk, A. A. 1962 Stability and transition of the free-convection layer along a vertical flat plate. Intl J. Heat Mass Transfer 5 (10), 903–914.CrossRefGoogle Scholar
Williamson, N., Armfield, S. W. & Kirkpatrick, M. P. 2012 Transition to oscillatory flow in a differentially heated cavity with a conducting partition. J. Fluid Mech. 693, 93–114.CrossRefGoogle Scholar
Xu, F., Patterson, J. C. & Lei, C. 2006 Experimental observations of the thermal flow around a square obstruction on a vertical wall in a differentially heated cavity. Exp. Fluids 40 (3), 364–371.CrossRefGoogle Scholar
Xu, F., Patterson, J. C. & Lei, C. 2009a Transient natural convection flows around a thin fin on the sidewall of a differentially heated cavity. J. Fluid Mech. 639, 261–290.CrossRefGoogle Scholar
Xu, F., Patterson, J. C. & Lei, C. 2009b Transition to a periodic flow induced by a thin fin on the sidewall of a differentially heated cavity. Intl J. Heat Mass Transfer 52 (3–4), 620–628.CrossRefGoogle Scholar
Xu, F., Patterson, J. C. & Lei, C. 2010 Temperature oscillations in a differentially heated cavity with and without a fin on the sidewall. Intl Commun. Heat Mass Transfer 37 (4), 350–359.CrossRefGoogle Scholar
Xu, F., Patterson, J. C. & Lei, C. 2011 Unsteady flow and heat transfer adjacent to the sidewall wall of a differentially heated cavity with a conducting and an adiabatic fin. Intl J. Heat Fluid Flow 32 (3), 680–687.CrossRefGoogle Scholar