Published online by Cambridge University Press: 09 July 2013
Resonance characteristics of tidal waves in a network are investigated with the linearized, one-dimensional shallow water equations. The network comprises a semi-enclosed main channel with an adjacent secondary channel at an arbitrary position. Water motion is forced by a prescribed incoming wave at the entrance of the main channel. The model is used to compute the ratio of sea surface height amplitude in the presence and absence of the secondary channel. Relevance lies in the possible construction of secondary channels to reduce tidal range in the main channel. When 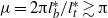 $\mu = 2\mathrm{\pi} { l}_{b}^{\ast } / { l}_{t}^{\ast } \gtrsim \mathrm{\pi} $ (
$\mu = 2\mathrm{\pi} { l}_{b}^{\ast } / { l}_{t}^{\ast } \gtrsim \mathrm{\pi} $ (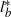 ${ l}_{b}^{\ast } $ being the length of the main channel,
${ l}_{b}^{\ast } $ being the length of the main channel, 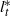 ${ l}_{t}^{\ast } $ the tidal wavelength) and friction is weak, it is found that reduction (amplification) of the tidal range occurs for secondary channels located less (more) than a quarter wavelength from the closed end of the main channel. Furthermore, a minimum is observed halfway between the closed end and the nodal point, and a maximum a quarter wavelength further seaward. With increasing friction and/or decreasing length of the main channel, amplitude ratios become less pronounced and depend weakly on the location of the secondary channel. The mechanism responsible for amplification or reduction of the sea surface height in the main channel is identified and explained in terms of the forced wave and waves radiating away from the secondary channel.
${ l}_{t}^{\ast } $ the tidal wavelength) and friction is weak, it is found that reduction (amplification) of the tidal range occurs for secondary channels located less (more) than a quarter wavelength from the closed end of the main channel. Furthermore, a minimum is observed halfway between the closed end and the nodal point, and a maximum a quarter wavelength further seaward. With increasing friction and/or decreasing length of the main channel, amplitude ratios become less pronounced and depend weakly on the location of the secondary channel. The mechanism responsible for amplification or reduction of the sea surface height in the main channel is identified and explained in terms of the forced wave and waves radiating away from the secondary channel.