Published online by Cambridge University Press: 06 September 2021
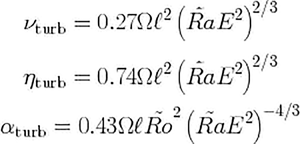
The magnetohydrodynamic (MHD) turbulence appears in engineering laboratory flows and is a common phenomenon in natural systems, e.g. stellar and planetary interiors and atmospheres and the interstellar medium. The applications in engineering are particularly interesting due to the recent advancement of tokamak devices, reaching very high plasma temperatures, thus giving hope for the production of thermonuclear fusion power. In the case of astrophysical applications, perhaps the main feature of the MHD turbulence is its ability to generate and sustain large-scale and small-scale magnetic fields. However, a crucial effect of the MHD turbulence is also the enhancement of large-scale diffusion via interactions of small-scale pulsations, i.e. the generation of the so-called turbulent viscosity and turbulent magnetic diffusivity, which typically exceed by orders of magnitude their molecular counterparts. The enhanced resistivity plays an important role in the turbulent dynamo process. Estimates of the turbulent electromotive force (EMF), including the so-called  $\alpha$-effect responsible for amplification of the magnetic energy and the turbulent magnetic diffusion are desired. Here, we apply the renormalization group technique to extract the final expression for the turbulent EMF from the fully nonlinear dynamical equations (Navier–Stokes, induction equation). The simplified renormalized set of dynamical equations, including the equations for the means and fluctuations, is derived and the effective turbulent coefficients such as the viscosity, resistivity, the
$\alpha$-effect responsible for amplification of the magnetic energy and the turbulent magnetic diffusion are desired. Here, we apply the renormalization group technique to extract the final expression for the turbulent EMF from the fully nonlinear dynamical equations (Navier–Stokes, induction equation). The simplified renormalized set of dynamical equations, including the equations for the means and fluctuations, is derived and the effective turbulent coefficients such as the viscosity, resistivity, the  $\alpha$-coefficient and the Lorentz-force coefficients are explicitly calculated. The results are also used to demonstrate the influence of magnetic fields on energy and helicity spectra of strongly turbulent flows, in particular the magnetic energy spectrum.
$\alpha$-coefficient and the Lorentz-force coefficients are explicitly calculated. The results are also used to demonstrate the influence of magnetic fields on energy and helicity spectra of strongly turbulent flows, in particular the magnetic energy spectrum.