Article contents
Release of a viscous power-law fluid over an inviscid ocean
Published online by Cambridge University Press: 17 April 2012
Abstract
We consider the two- and three-dimensional spreading of a finite volume of viscous power-law fluid released over a denser inviscid fluid and subject to gravitational and capillary forces. In the case of gravity-driven spreading, with a power-law fluid having strain rate proportional to stress to the power  , there are similarity solutions with the extent of the current being proportional to
, there are similarity solutions with the extent of the current being proportional to  in the two-dimensional case and
in the two-dimensional case and 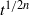 in the three-dimensional case. Perturbations from these asymptotic states are shown to retain their initial shape but to decay relatively as
in the three-dimensional case. Perturbations from these asymptotic states are shown to retain their initial shape but to decay relatively as 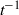 in the two-dimensional case and
in the two-dimensional case and 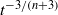 in the three-dimensional case. The former is independent of
in the three-dimensional case. The former is independent of  , whereas the latter gives a slower rate of relative decay for fluids that are more shear-thinning. In cases where the layer is subject to a constraining surface tension, we determine the evolution of the layer towards a static state of uniform thickness in which the gravitational and capillary forces balance. The asymptotic form of this convergence is shown to depend strongly on
, whereas the latter gives a slower rate of relative decay for fluids that are more shear-thinning. In cases where the layer is subject to a constraining surface tension, we determine the evolution of the layer towards a static state of uniform thickness in which the gravitational and capillary forces balance. The asymptotic form of this convergence is shown to depend strongly on  , with rapid finite-time algebraic decay in shear-thickening cases, large-time exponential decay in the Newtonian case and slow large-time algebraic decay in shear-thinning cases.
, with rapid finite-time algebraic decay in shear-thickening cases, large-time exponential decay in the Newtonian case and slow large-time algebraic decay in shear-thinning cases.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 11
- Cited by


