Article contents
The relaxation time for viscous and porous gravity currents following a change in flux
Published online by Cambridge University Press: 24 May 2017
Abstract
The equilibration time  $\unicode[STIX]{x1D70F}$ in response to a change in flux from
$\unicode[STIX]{x1D70F}$ in response to a change in flux from 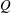 $Q$ to
$Q$ to 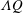 $\unicode[STIX]{x1D6EC}Q$ after an injection period
$\unicode[STIX]{x1D6EC}Q$ after an injection period 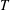 $T$ applied to either a low-Reynolds-number gravity current or one propagating through a porous medium, in both axisymmetric and one-dimensional geometries, is shown to be of the form
$T$ applied to either a low-Reynolds-number gravity current or one propagating through a porous medium, in both axisymmetric and one-dimensional geometries, is shown to be of the form 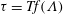 $\unicode[STIX]{x1D70F}=Tf(\unicode[STIX]{x1D6EC})$, independent of all the remaining physical parameters. Numerical solutions are used to investigate
$\unicode[STIX]{x1D70F}=Tf(\unicode[STIX]{x1D6EC})$, independent of all the remaining physical parameters. Numerical solutions are used to investigate 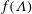 $f(\unicode[STIX]{x1D6EC})$ for each of these situations and compare very well with experimental results in the case of an axisymmetric current propagating over a rigid horizontal boundary. Analysis of the relaxation towards self-similarity provides an illuminating connection between the excess (deficit) volume from early times and an asymptotically equivalent shift in time origin, and hence a good quantitative estimate of
$f(\unicode[STIX]{x1D6EC})$ for each of these situations and compare very well with experimental results in the case of an axisymmetric current propagating over a rigid horizontal boundary. Analysis of the relaxation towards self-similarity provides an illuminating connection between the excess (deficit) volume from early times and an asymptotically equivalent shift in time origin, and hence a good quantitative estimate of  $\unicode[STIX]{x1D70F}$. The case
$\unicode[STIX]{x1D70F}$. The case 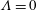 $\unicode[STIX]{x1D6EC}=0$ of equilibration after ceasing injection at time
$\unicode[STIX]{x1D6EC}=0$ of equilibration after ceasing injection at time 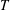 $T$ is a singular limit. Extensions to high-Reynolds-number currents and to the case of a constant-volume release followed by constant-flux injection are discussed briefly.
$T$ is a singular limit. Extensions to high-Reynolds-number currents and to the case of a constant-volume release followed by constant-flux injection are discussed briefly.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 6
- Cited by



