Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T10:46:55.143Z Has data issue: false hasContentIssue false
  • English
  • Français

The relative-velocity version of the Morison equation for obstacle arrays in combined steady, low and high frequency motion

Published online by Cambridge University Press:  07 March 2018

H. Santo Open the ORCID record for H. Santo [Opens in a new window] ,
P. H. Taylor ,
C. H. K. Williamson  and
Y. S. Choo
H. Santo*
Affiliation:
Office of the Deputy President (Research and Technology), National University of Singapore, Singapore 117576, Singapore
P. H. Taylor
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
C. H. K. Williamson
Affiliation:
School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Y. S. Choo
Affiliation:
Centre for Offshore Research and Engineering, Department of Civil and Environmental Engineering, National University of Singapore, Singapore 117576, Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper revisits the problem of forces on obstacle arrays in combined waves, an in-line steady current and structural dynamic motions. The intended application is the design and re-assessment of dynamically responding offshore platforms. Planar grids of perforated plates are moved in forced motion on three scales through otherwise stationary water. A new analytical wave–current–structure blockage model is developed by building on the existing wave–current blockage model presented by Santo et al. (J. Fluid Mech., vol. 739, 2014b, pp. 143–178) using a similar set of experiments but with forced motion on two scales. The new model, which is an improved Morison relative-velocity formulation, is tested against the experimental data for a range of structural to wave oscillation frequency ratios, 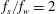$f_{s}/f_{w}=2$, 2.5 and 3. For relatively small current speed (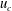$u_{c}$) and oscillatory structural velocity (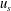$u_{s}$) compared with the oscillatory wave velocity (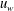$u_{w}$), the drag force time history on grids is well approximated by a summation of the wave drag and the current drag components independently, without a 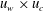$u_{w}\times u_{c}$ cross-term, consistent with the previous model. The wave drag component contains an additional 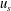$u_{s}$ contribution, while the current drag component may or may not contain an additional 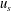$u_{s}$ contribution depending on 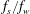$f_{s}/f_{w}$. The measured drag force is observed to be asymmetric in time due to biasing from the mean flow. This is supported by numerical simulation using a porous block as a numerical model of the grids, although the simulated force asymmetry is weaker. All these effects can be sufficiently accounted for in the analytical model. The new model is shown to fit the variation of the experimental forces and force harmonics in time well for a wide range of cases, requiring only calibration of the Morison type drag and inertia coefficients. In contrast, the industry-standard version of the Morison relative-velocity formulation cannot reproduce the variation of the measured force in time, so present practice should be regarded as inadequate for combined steady, low frequency and high frequency motion acting on obstacle arrays.

JFM classification

Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 188 - 214
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

American Petroleum Institute 2000 Recommended practice for planning, designing, and constructing fixed offshore platforms: working stress design. In API RP2A-WSD 21st Edition with Erratas and Supplements, vol. 1, pp. 130–132. American Petroleum Institute.Google Scholar
Burrows, R., Tickell, R. G., Hames, D. & Najafian, G. 1997 Morison wave force coefficients for application to random seas. Appl. Ocean Res. 19 (3–4), 183–199.CrossRefGoogle Scholar
Chen, H. & Christensen, E. D. 2016 Investigations on the porous resistance coefficients for fishing net structures. J. Fluids Struct. 65, 76–107.CrossRefGoogle Scholar
Kristiansen, T. & Faltinsen, O. M. 2012 Modelling of current loads on aquaculture net cages. J. Fluids Struct. 34, 218–235.Google Scholar
Lighthill, J. 1986 Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 173, 667–681.Google Scholar
Moe, G. & Verley, R. L. P. 1980 Hydrodynamic damping of offshore structures in waves and currents. In Offshore Technology Conference, OTC 3798. Offshore Technology Conference.Google Scholar
Morison, J. R., O’Brien, M. P., Johnson, J. W. & Schaaf, S. A. 1950 The force exerted by surface waves on piles. J. Petrol. Tech. 2 (5), 149–154.Google Scholar
Santo, H., Stagonas, D., Buldakov, E. & Taylor, P. H. 2017 Current blockage in sheared flow: experiments and numerical modelling of regular waves and strongly sheared current through a space-frame structure. J. Fluids Struct. 70, 374–389.Google Scholar
Santo, H., Taylor, P. H., Bai, W. & Choo, Y. S. 2014a Blockage effects in wave and current: 2D planar simulations of combined regular oscillations and steady flow through porous blocks. Ocean Engng 88, 174–186.Google Scholar
Santo, H., Taylor, P. H., Bai, W. & Choo, Y. S. 2015 Current blockage in a numerical wave tank: 3D simulations of regular waves and current through a porous tower. Comput. Fluids 115, 256–269.CrossRefGoogle Scholar
Santo, H., Taylor, P. H., Day, A. H., Nixon, E. & Choo, Y. S. 2018 Current blockage and extreme forces on a jacket model in focussed wave groups with current. J. Fluids Struct. 78C, 24–35.CrossRefGoogle Scholar
Santo, H., Taylor, P. H., Williamson, C. H. K. & Choo, Y. S. 2014b Current blockage experiments: force time histories on obstacle arrays in combined steady and oscillatory motion. J. Fluid Mech. 739, 143–178.CrossRefGoogle Scholar
Shafiee-Far, M., Massie, W. W. & Vugts, J. H. 1996 The validity of Morison equation extensions. In Offshore Technology Conference, OTC 8064. Offshore Technology Conference.Google Scholar
Sumer, B. M. & Fredsøe, J. 2006 Hydrodynamics Around Cylindrical Structures. World Scientific.Google Scholar
Taylor, P. H. 1991 Current blockage: reduced forces on offshore space-frame structures. In Offshore Technology Conference, OTC 6519. Offshore Technology Conference.Google Scholar
Taylor, P. H., Santo, H. & Choo, Y. S. 2013 Current blockage: reduced Morison forces on space frame structures with high hydrodynamic area, and in regular waves and current. Ocean Engng 57, 11–24.CrossRefGoogle Scholar
Williamson, C. H. K. 1985 In-line response of a cylinder in oscillatory flow. Appl. Ocean Res. 7 (2), 97–106.Google Scholar
Zhao, Y. P., Bi, C. W., Dong, G. H., Gui, F. K., Cui, Y., Guan, C. T. & Xu, T. J. 2013 Numerical simulation of the flow around fishing plane nets using the porous media model. Ocean Engng 62, 25–37.CrossRefGoogle Scholar