Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T11:22:13.906Z Has data issue: false hasContentIssue false
  • English
  • Français

The regular reflection→Mach reflection transition in unsteady flow over convex surfaces

Published online by Cambridge University Press:  19 December 2017

M. Geva ,
O. Ram  and
O. Sadot Open the ORCID record for O. Sadot [Opens in a new window]
M. Geva
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
O. Ram
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
O. Sadot*
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The non-stationary transition from regular reflection (RR) to Mach reflection (MR) over convex segments has been the focus of many recent studies. Until recently, the problem was thought to be very complicated because it was believed that many parameters such as the radius of curvature, initial angle and geometrical shape of the reflecting surface influenced this process. In this study, experiments and inviscid numerical computations were performed in air (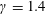$\unicode[STIX]{x1D6FE}=1.4$) at an incident shock-wave Mach number of 1.3. The incident shock waves were reflected over cylindrical and elliptical convex surfaces. The computations were validated by high-resolution experiments, which enabled the detection of features in the flow having characteristic lengths as small as 0.06 mm. Therefore, the RR →MR transition and Mach stem growth were successfully validated in the early stages of the Mach stem formation and closer to the surface than ever before. The evolution of the RR, the transition to MR and the Mach stem growth were found to depend only on the radius of the reflecting surface. The reflected shock wave adjusts itself to the changing angles of the reflecting surface. This feature, which was demonstrated at Mach numbers 1.3 and 1.5, distinguishes the unsteady case from the self-similar pseudo-steady case and requires the formulation of the conservation equations. A modification of the standard two-shock theory (2ST) is presented to predict the flow properties behind a shock wave that propagates over convex surfaces. Until recently, the determination of the time-dependent flow properties was possible solely by numerical computations. Moreover, this derivation explains the controversial issue on the delay in the transition from the RR to the MR that was observed by many researchers. It turns out that the entire RR evolution and the particular moment of transition to MR, are based on the essential ‘no-penetration’ condition of the flow. Therefore, we proposed a simple geometrical criterion for the RR →MR transition.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 837 , 25 February 2018 , pp. 48 - 79
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

ANSYS®Academic Research, Release 15.0, Theory Guide, ANSYS, Inc, 2013.Google Scholar
Barth, T. & Jespresen, D. 1989 The design and application of upwind schemes on unstructured meshes. In 27th Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics.Google Scholar
Ben-Dor, G. 2007 Shock Wave Reflection Phenomena. Springer.Google Scholar
Ben-Dor, G. & Takayama, K. 1986 Application of steady shock polars to unsteady shock wave reflections. AIAA J. 24, 682–684.Google Scholar
Bryson, A. E. & Gross, R. W. F. 1961 Diffraction of strong shocks by cones, cylinders, and spheres. J. Fluid Mech. 10 (01), 1–16.Google Scholar
Geva, M., Ram, O. & Sadot, O. 2013 The non-stationary hysteresis phenomenon in shock wave reflections. J. Fluid Mech. 732, R1.Google Scholar
Hakkaki-Fard, A. & Timofeev, E. 2012 On numerical techniques for determination of the sonic point in unsteady inviscid shock reflections. Intl J. Aero. Innov. 4 (1–2), 41–52.Google Scholar
Han, Z. Y. 1991 Shock dynamic description of reflected shock waves. In Proc. 18th Intl Symp. Shock Waves, Sendai, Japan, pp. 299–304. Springer.Google Scholar
Han, Z. & Yin, X. 1993 Shock Dynamics: Fluid Mechanics and its Application, vol. 11. Kluwer Academic.Google Scholar
Heilig, W. H. 1969 Diffraction of a shock wave by a cylinder. Phys. Fluids 12 (5), I-154.Google Scholar
Holmes, D. & Connell, S. 1989 Solution of the 2D Navier–Stokes equations on unstructured adaptive grids. In 9th Computational Fluid Dynamics Conference, American Institute of Aeronautics and Astronautics.Google Scholar
Hornung, H. G., Oertel, H. Jr & Sandeman, R. J. 1979 Transition to Mach reflection of shock waves in steady and pseudo steady flow with and without relaxation. J. Fluid Mech. 90, 541–560.Google Scholar
Hryniewicki, M. K., Gottlieb, J. J. & Groth, C. P. T. 2016 Transition boundary between regular and Mach reflections for a moving shock interacting with a wedge in inviscid and polytropic air. Shock Waves 27 (4), 523–550.Google Scholar
Itoh, S., Okazaki, N. & Itaya, M. 1981 On the transition between regular and Mach reflection in truly non-stationary flows. J. Fluid Mech. 108, 383–400.Google Scholar
Jameson, A., Schmidt, W. & Turkel, E. 1981 Numerical solution of the euler equations by finite volume methods schemes. In 14th Fluid and Plasma Dynamic Conference, vol. M, pp. 1–19. American Institute of Aeronautics and Astronautics.Google Scholar
Kleine, H., Timofeev, E., Hakkaki-Fard, A. & Skews, B. 2014 The influence of Reynolds number on the triple point trajectories at shock reflection off cylindrical surfaces. J. Fluid Mech. 740, 47–60.Google Scholar
Li, H. D.1988 Study of transition criteria from RR to MR in truly nonstationary flows. Thesis, Univ. of Science and Technology of China.Google Scholar
Lock, G. D. & Dewey, J. M. 1989 An experimental investigation of the sonic criterion for transition from regular to Mach reflection of weak shock waves. Exp. Fluids 7, 289–292.Google Scholar
Milton, B. E. 1975 Mach reflection using ray-shock theory. AIAA J. 13 (11), 1531–1533.Google Scholar
von Neumann, J.1943a Oblique reflection of shocks. Explos. Res. Rep. 12, Navy Dept., Bureau of Ordinance, Washington, DC, USA.Google Scholar
von Neumann, J.1943b Refraction, intersection and reflection of shock waves. NAVORD Rep. 203-45, Navy Dept., Bureau of rdinance, Washington, DC, USA.Google Scholar
Pratt, V. 1987 Direct least-squares fitting of algebraic surfaces. Comput. Graph. 21 (4), 145–152.Google Scholar
Ram, O., Geva, M. & Sadot, O. 2015 High spatial and temporal resolution study of shock wave reflection over a coupled convex–concave cylindrical surface. J. Fluid Mech. 768, 219–239.Google Scholar
Rausch, R. D., Batina, J. T. & Yang, H. T. Y. 1992 Spatial adaptation of unstructured meshes for unsteady aerodynamic flow computations. AIAA J. 30 (5), 1243–1251.Google Scholar
Shirouzu, M. & Glass, I. I. 1986 Evaluation of assumptions and criteria in pseudostationary oblique shock-wave reflections. Proc. R. Soc. Lond. A 406 (1830), 75–92.Google Scholar
Skews, B. & Kleine, H. 2009 Unsteady flow diagnostics using weak perturbations. Exp. Fluids 46, 65–76.Google Scholar
Skews, B. W. & Blitterswijk, A. 2011 Shock wave reflection off coupled surfaces. Shock Waves 21, 491–498.Google Scholar
Skews, B. W. & Kleine, H. 2010 Shock wave interaction with convex circular cylindrical surfaces. J. Fluid Mech. 654, 195–205.Google Scholar
Takayama, K. & Sasaki, M. 1983 Effects of radius of curvature and initial angle on the shock transition over concave and convex walls. Reports of the Institute of High Speed Mechanic 46, 1–30.Google Scholar
Timofeev, E., Skews, B. W., Voinovich, P. A. & Takayama, K. 1999 The influence of unsteadiness and three-dimensionality on regular-to-Mach reflection transitions: a high-resolution study. In Proc. 22nd Int. Symp. Shock Waves, Imperial College, London, vol. 2, pp. 1231–1236. University of Southampton.Google Scholar
Vignati, F. & Guardone, A. 2016 Leading edge reflection patterns for cylindrical converging shock waves over convex obstacles. Phys. Fluids 28 (9), 096103.Google Scholar
Whitham, G. B. 1968 A note on shock dynamics relative to a moving frame. J. Fluid Mech. 31 (3), 449–453.Google Scholar