Published online by Cambridge University Press: 22 July 2019
We describe the long-term dynamics of sustained stratified shear flows in the laboratory. The stratified inclined duct (SID) experiment sets up a two-layer exchange flow in an inclined duct connecting two reservoirs containing salt solutions of different densities. This flow is primarily characterised by two non-dimensional parameters: the tilt angle of the duct with respect to the horizontal, 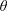 $\unicode[STIX]{x1D703}$ (a few degrees at most), and the Reynolds number
$\unicode[STIX]{x1D703}$ (a few degrees at most), and the Reynolds number 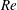 $Re$, an input parameter based on the density difference driving the flow. The flow can be sustained with constant forcing over arbitrarily long times and exhibits a wealth of dynamical behaviours representative of geophysically relevant sustained stratified shear flows. Varying
$Re$, an input parameter based on the density difference driving the flow. The flow can be sustained with constant forcing over arbitrarily long times and exhibits a wealth of dynamical behaviours representative of geophysically relevant sustained stratified shear flows. Varying 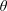 $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and 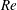 $Re$ leads to four qualitatively different regimes: laminar flow; mostly laminar flow with finite-amplitude, travelling Holmboe waves; spatio-temporally intermittent turbulence with substantial interfacial mixing; and sustained, vigorous interfacial turbulence (Meyer & Linden, J. Fluid Mech., vol. 753, 2014, pp. 242–253). We seek to explain the scaling of the transitions between flow regimes in the two-dimensional plane of input parameters
$Re$ leads to four qualitatively different regimes: laminar flow; mostly laminar flow with finite-amplitude, travelling Holmboe waves; spatio-temporally intermittent turbulence with substantial interfacial mixing; and sustained, vigorous interfacial turbulence (Meyer & Linden, J. Fluid Mech., vol. 753, 2014, pp. 242–253). We seek to explain the scaling of the transitions between flow regimes in the two-dimensional plane of input parameters  $(\unicode[STIX]{x1D703},Re)$. We improve upon previous studies of this problem by providing a firm physical basis and non-dimensional scaling laws that are mutually consistent and in good agreement with the empirical transition curves we inferred from 360 experiments spanning
$(\unicode[STIX]{x1D703},Re)$. We improve upon previous studies of this problem by providing a firm physical basis and non-dimensional scaling laws that are mutually consistent and in good agreement with the empirical transition curves we inferred from 360 experiments spanning 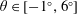 $\unicode[STIX]{x1D703}\in [-1^{\circ },6^{\circ }]$ and
$\unicode[STIX]{x1D703}\in [-1^{\circ },6^{\circ }]$ and 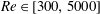 $Re\in [300,5000]$. To do so, we employ state-of-the-art simultaneous volumetric measurements of the density field and the three-component velocity field, and analyse these experimental data using time- and volume-averaged potential and kinetic energy budgets. We show that regime transitions are caused by an increase in the non-dimensional time- and volume-averaged kinetic energy dissipation within the duct, which scales with
$Re\in [300,5000]$. To do so, we employ state-of-the-art simultaneous volumetric measurements of the density field and the three-component velocity field, and analyse these experimental data using time- and volume-averaged potential and kinetic energy budgets. We show that regime transitions are caused by an increase in the non-dimensional time- and volume-averaged kinetic energy dissipation within the duct, which scales with 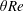 $\unicode[STIX]{x1D703}Re$ at high enough angles. As the power input scaling with
$\unicode[STIX]{x1D703}Re$ at high enough angles. As the power input scaling with 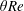 $\unicode[STIX]{x1D703}Re$ is increased above zero, the two-dimensional, parallel-flow dissipation (power output) increases to close the budget through an increase in the magnitude of the exchange flow, incidentally triggering Holmboe waves above a certain threshold in interfacial shear. However, once the hydraulic limit of two-layer exchange flows is reached, two-dimensional dissipation plateaus and three-dimensional dissipation at small scales (turbulence) takes over, at first intermittently, and then steadily, in order to close the budget and follow the
$\unicode[STIX]{x1D703}Re$ is increased above zero, the two-dimensional, parallel-flow dissipation (power output) increases to close the budget through an increase in the magnitude of the exchange flow, incidentally triggering Holmboe waves above a certain threshold in interfacial shear. However, once the hydraulic limit of two-layer exchange flows is reached, two-dimensional dissipation plateaus and three-dimensional dissipation at small scales (turbulence) takes over, at first intermittently, and then steadily, in order to close the budget and follow the 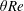 $\unicode[STIX]{x1D703}Re$ scaling. This general understanding of regime transitions and energetics in the SID experiment may serve as a basis for the study of more complex sustained stratified shear flows found in the natural environment.
$\unicode[STIX]{x1D703}Re$ scaling. This general understanding of regime transitions and energetics in the SID experiment may serve as a basis for the study of more complex sustained stratified shear flows found in the natural environment.