Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Grayer II, Hezekiah
Yalim, Jason
Welfert, Bruno D.
and
Lopez, Juan M.
2021.
Stably stratified square cavity subjected to horizontal oscillations: responses to small amplitude forcing.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Boury, S.
Sibgatullin, I.
Ermanyuk, E.
Shmakova, N.
Odier, P.
Joubaud, S.
Maas, L.R.M.
and
Dauxois, T.
2021.
Vortex cluster arising from an axisymmetric inertial wave attractor.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
Lopez, Juan M.
Shen, Jie
Welfert, Bruno D.
and
Wu, Ke
2022.
Boundary-confined waves in a librating cube.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Wu, Ke
Huang, Fukeng
and
Shen, Jie
2022.
A new class of higher-order decoupled schemes for the incompressible Navier-Stokes equations and applications to rotating dynamics.
Journal of Computational Physics,
Vol. 458,
Issue. ,
p.
111097.
Wu, Ke
Welfert, Bruno D.
and
Lopez, Juan M.
2022.
Reflections and focusing of inertial waves in a tilted librating cube.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Yalim, Jason
Welfert, Bruno D.
and
Lopez, Juan M.
2022.
Oblique instability of a stratified oscillatory boundary layer.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Welfert, Bruno D.
Lopez, Juan M.
and
Wu, Ke
2023.
Inertial wave attractors in rapidly rotating tilted cuboids.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 479,
Issue. 2272,
Subbotin, Stanislav
and
Shiryaeva, Mariya
2023.
Inertial Wave Beam Path in a Non-uniformly Rotating Cylinder with Sloping Ends.
Microgravity Science and Technology,
Vol. 35,
Issue. 3,
Wu, Ke
Welfert, Bruno D.
and
Lopez, Juan M.
2023.
Inertial wave attractors in librating cuboids.
Journal of Fluid Mechanics,
Vol. 973,
Issue. ,
Shiryaeva, Mariya
Subbotina, Mariya
and
Subbotin, Stanislav
2024.
Linear and Non-Linear Dynamics of Inertial Waves in a Rotating Cylinder with Antiparallel Inclined Ends.
Fluid Dynamics & Materials Processing,
Vol. 20,
Issue. 4,
p.
787.
Subbotin, Stanislav
and
Shiryaeva, Mariya
2025.
Inertial Wave Attractors in Librating Cylinders: Axisymmetric versus Nonaxisymmetric Ends.
Microgravity Science and Technology,
Vol. 37,
Issue. 1,
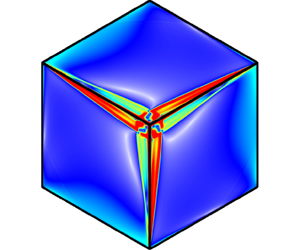
 $\text{E}=10^{-7}$) and small libration amplitude (
$\text{E}=10^{-7}$) and small libration amplitude ( $\unicode[STIX]{x1D716}=10^{-7}$) exhibit complicated spatio-temporal structure that is remarkably well described by considerations of the inviscid reflections of wavebeams over the whole range of libration frequencies from zero to twice the mean rotation rate of the cube.
$\unicode[STIX]{x1D716}=10^{-7}$) exhibit complicated spatio-temporal structure that is remarkably well described by considerations of the inviscid reflections of wavebeams over the whole range of libration frequencies from zero to twice the mean rotation rate of the cube.