No CrossRef data available.
Article contents
Reflection of a centred compression wave
Published online by Cambridge University Press: 26 March 2024
Abstract
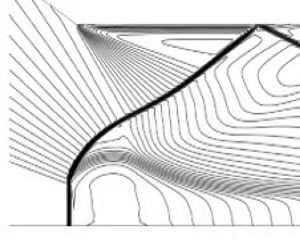
The reflection of a centred compression wave, that converges to a single point on the reflecting surface, is studied and compared with shock reflection. It is shown that the double solution domain, with both regular and Mach reflections, of centred compression wave reflection is enlarged with respect to shock reflection. For centred compression wave reflection, no clear triple point structure exists, and instead, the reflected shock and Mach stem form a smooth curved shock wave. Moreover, the relative Mach stem height, though decreasing almost linearly with the relative wedge trailing edge height as in shock reflection, has a lower bound when the trailing edge height increases, meaning that wedge height variation induced transition, that occurs in shock reflection, does not exist. The existence of this lower bound is due to the fact that beyond a certain value of the wedge trailing edge height, the wedge trailing edge encounters the wedge lower surface that generates the centred compression wave. The present study expands our knowledge of shock reflection, and may be useful for supersonic inlet design.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


