Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T04:47:37.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduced-order unsteady aerodynamic models at low Reynolds numbers

Published online by Cambridge University Press:  29 April 2013

Steven L. Brunton ,
Clarence W. Rowley  and
David R. Williams
Steven L. Brunton*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Clarence W. Rowley
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
David R. Williams
Affiliation:
Department of Mechanical, Materials, and Aerospace Engineering, Illinois Institute of Technology, Chicago, IL 60616, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we develop reduced-order models for the unsteady lift on a pitching and plunging aerofoil over a range of angles of attack. In particular, we analyse the pitching and plunging dynamics for two cases: a two-dimensional flat plate at 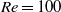$\mathit{Re}= 100$ using high-fidelity direct numerical simulations and a three-dimensional NACA 0006 aerofoil at 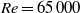$\mathit{Re}= 65\hspace{0.167em} 000$ using wind-tunnel measurements. Models are obtained at various angles of attack and they are verified against measurements using frequency response plots and large-amplitude manoeuvres. These models provide a low-dimensional balanced representation of the relevant unsteady fluid dynamics. In simulations, flow structures are visualized using finite-time Lyapunov exponents. A number of phenomenological trends are observed, both in the data and in the models. As the base angle of attack increases, the boundary layer begins to separate, resulting in a decreased quasi-steady lift coefficient slope and a delayed relaxation to steady state at low frequencies. This extends the low-frequency range of motions that excite unsteady effects, meaning that the quasi-steady approximation is not valid until lower frequencies than are predicted by Theodorsen’s classical inviscid model. In addition, at small angles of attack, the lift coefficient rises to the steady-state value after a step in angle, while at larger angles of attack, the lift coefficient relaxes down to the steady-state after an initially high lift state. Flow visualization indicates that this coincides with the formation and convection of vortices at the leading edge and trailing edge. As the angle of attack approaches the critical angle for vortex shedding, the poles and zeros of the model approach the imaginary axis in the complex plane, and some zeros cross into the right half plane. This has significant implications for active flow control, which are discussed. These trends are observed in both simulations and wind-tunnel data.

JFM classification

Aerodynamics: Aerodynamics Flow Control: Flow Control Nonlinear Dynamical Systems: Low-dimensional models
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 203 - 233
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahuja, S. & Rowley, C. W. 2010 Feedback control of unstable steady states of flow past a flat plate using reduced-order estimators. J. Fluid Mech. 645, 447–478.Google Scholar
Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Apkarian, P., Pellanda, P. & Tuan, H. D. 2000 Mixed ${h}_{2} / {h}_{\infty } $ multi-channel linear parameter-varying control in discrete time. Syst. Control Lett. 41, 333–346.Google Scholar
Bagheri, S., Brandt, L. & Henningson, D. S. 2009 Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.Google Scholar
Bamieh, B. & Giarré, L. 2002 Identification of linear parameter varying models. Intl J. Robust Nonlinear Control 12, 841–853.Google Scholar
Birch, J. & Dickinson, M. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412, 729–733.Google Scholar
Brennen, C. E. 1982 A review of added mass and fluid inertial forces. Tech. Rep. CR 82.010. Naval Civil Engineering Laboratory.Google Scholar
Brunton, S. L. 2012 Unsteady aerodynamic models for agile flight at low Reynolds numbers. PhD thesis, Princeton University.Google Scholar
Brunton, S. L. & Rowley, C. W. 2010 Fast computation of FTLE fields for unsteady flows: a comparison of methods. Chaos 20, 017503.CrossRefGoogle Scholar
Brunton, S. L. & Rowley, C. W. 2013 Empirical state-space representations for Theodorsen’s lift model. J. Fluids Struct. 38, 174–186.CrossRefGoogle Scholar
Buchholz, J. H. J. & Smits, A. J. 2008 The wake structure and thrust performance of a rigid, low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.CrossRefGoogle ScholarPubMed
Colonius, T. & Taira, K. 2008 A fast immersed boundary method using a nullspace approach and multi-domain far-field boundary conditions. Comput. Meth. Appl. Mech. Engng 197, 2131–2146.Google Scholar
Daniel, T. L. 1984 Unsteady aspects of aquatic locomotion. Am. Zool. 24 (1), 121–134.Google Scholar
Dullerud, G. E. & Paganini, F. 2000 A Course in Robust Control Theory: A Convex Approach. Springer.Google Scholar
Edwards, J. W. 1977 Unsteady Aerodynamic Modeling and Active Aeroelastic Control. SUDARR 504. Stanford University.Google Scholar
Eldredge, J. D., Wang, C. & Ol, M. V. 2009 A computational study of a canonical pitch-up, pitch-down wing maneuver. AIAA Paper 2009-3687, 39th Fluid Dynamics Conference.Google Scholar
Franco, E., Pekarek, D. N., Peng, J. & Dabiri, J. O. 2007 Geometry of unsteady fluid transport during fluid–structure interactions. J. Fluid Mech. 589, 125–145.Google Scholar
Green, M. A., Rowley, C. W. & Haller, G. 2007 Detection of Lagrangian coherent structures in 3D turbulence. J. Fluid Mech. 572, 111–120.Google Scholar
Green, M. A., Rowley, C. W. & Smits, A. J. 2011 The unsteady three-dimensional wake produced by a trapezoidal pitching panel. J. Fluid Mech. 685, 117–145.Google Scholar
Green, M. A. & Smits, A. J. 2008 Effects of three-dimensionality on thrust production by a pitching panel. J. Fluid Mech. 615, 211–220.Google Scholar
Haller, G. 2002 Lagrangian coherent structures from approximate velocity data. Phys. Fluids 14 (6), 1851–1861.CrossRefGoogle Scholar
Haller, G. 2004 Exact theory of unsteady separation for two-dimensional flows. J. Fluid Mech. 512, 257–311.Google Scholar
Ilak, M. & Rowley, C. W. 2008 Modeling of transitional channel flow using balanced proper orthogonal decomposition. Phys. Fluids 20, 034103.CrossRefGoogle Scholar
Illingworth, S. J., Morgans, A. S. & Rowley, C. W. 2010 Feedback control of flow resonances using balanced reduced-order models. J. Sound Vib. 330 (8), 1567–1581.CrossRefGoogle Scholar
Juang, J. N. & Pappa, R. S. 1985 An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control Dyn. 8 (5), 620–627.CrossRefGoogle Scholar
Juang, J. N., Phan, M., Horta, L. G. & Longman, R. W. 1991 Identification of observer/Kalman filter Markov parameters: theory and experiments. Technical Memorandum 104069. NASA.CrossRefGoogle Scholar
Kaplan, S. M., Altman, A. & Ol, M. 2007 Wake vorticity measurements for low aspect ratio wings at low Reynolds number. J. Aircraft 44 (1), 241–251.Google Scholar
von Kármán, T. & Sears, W. R. 1938 Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 5 (10), 379–390.Google Scholar
Kerstens, W., Pfeiffer, J., Williams, D., King, R. & Colonius, T. 2011 Closed-loop control of lift for longitudinal gust suppression at low Reynolds numbers. AIAA J. 49 (8), 1721–1728.Google Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.Google Scholar
Lesieutre, D. J., Reisenthel, P. H. & Dillenius, M. F. E. 1994 A practical approach for calculating aerodynamic indicial functions with a Navier–Stokes solver. AIAA Paper 94-0059, 32nd Aerospace Sciences Meeting.Google Scholar
Ljung, L. 1999 System Identification: Theory for the User. Prentice Hall.Google Scholar
Ma, Z., Ahuja, S. & Rowley, C. W. 2011 Reduced order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 25 (1), 233–247.Google Scholar
Ol, M. V., Altman, A., Eldredge, J. D., Garmann, D. J. & Lian, Y. 2010 Résumé of the AIAA FDTC low Reynolds number discussion group’s canaonical cases. AIAA Paper 2010-1085, 48th Aerospace Sciences Meeting.Google Scholar
Or, A. C. & Speyer, J. L. 2010 Empirical pseudo-balanced model reduction and feedback control of weakly nonlinear convection patterns. J. Fluid Mech. 662, 36–65.Google Scholar
Peng, J. & Dabiri, J. O. 2008 The ‘upstream wake’ of swimming and flying animals and its correlation with propulsive efficiency. J. Expl Biol. 211, 2669–2677.Google Scholar
Pines, D. J. & Bohorquez, F. 2006 Challenges facing future micro-air-vehicle development. J. Aircraft 43 (2), 290–305.CrossRefGoogle Scholar
Pullin, D. I. & Wang, Z. J. 2004 Unsteady forces on an accelerating plate and application to hovering insect flight. J. Fluid Mech. 509, 1–21.Google Scholar
Rowley, C. W. 2005 Model reduction for fluids using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15 (3), 997–1013.Google Scholar
Ruelle, D. & Takens, F. 1971 On the nature of turbulence. Commun. Math. Phys. 20, 167–192.Google Scholar
Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206 (23), 4191–4208.Google Scholar
Shadden, S. C., Katija, K., Rosenfeld, M., Marsden, J. E. & Dabiri, J. O. 2007 Transport and stirring induced by vortex formation. J. Fluid Mech. 593, 315–331.Google Scholar
Shadden, S. C., Lekien, F. & Marsden, J. E. 2005 Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 212, 271–304.Google Scholar
Surana, A., Grunberg, O. & Haller, G. 2006 Exact theory of three-dimensional flow separation. Part 1. Steady separation. J. Fluid Mech. 564, 57–103.Google Scholar
Taira, K. & Colonius, T. 2007 The immersed boundary method: a projection approach. J. Comput. Phys. 225 (2), 2118–2137.Google Scholar
Taira, K. & Colonius, T. 2009 Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers. J. Fluid Mech. 623, 187–207.Google Scholar
Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. Tech. Rep. 496. NACA.Google Scholar
Torres, G. E. & Mueller, T. J. 2004 Low-aspect-ratio wing aerodynamics at low Reynolds numbers. AIAA J. 42 (5), 865–873.Google Scholar
Triantafyllou, G. S., Triantafyllou, M. S. & Grosenbaugh, M. A. 1993 Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 7, 205–224.CrossRefGoogle Scholar
Truong, K. V. & Tobak, M. 1990 Indicial response approach derived from Navier–Stokes equations. Part 1. Time-invariant equilibrium state. Technical Memorandum 102856. NASA.Google Scholar
Videler, J. J., Samhuis, E. J. & Povel, G. D. E. 2004 Leading-edge vortex lifts swifts. Science 306, 1960–1962.Google Scholar
Wagner, H. 1925 Über die Entstehung des dynamischen Auftriebes von Tragflügeln. Z. Angew. Math. Mech. 5 (1), 17–35.Google Scholar
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–210.Google Scholar
Weldon, M., Peacock, T., Jacobs, G. B., Helu, M. & Haller, G. 2008 Experimental and numerical investigation of the kinematic theory of unsteady separation. J. Fluid Mech. 611, 1–11.Google Scholar
Wilson, M. M., Peng, J., Dabiri, J. O. & Eldredge, J. D. 2009 Lagrangian coherent structures in low Reynolds number swimming. J. Phys. C: Matt. 21 (20), 204105.Google ScholarPubMed
Zbikowski, R. 2002 On aerodynamic modelling of an insect-like flapping wing in hover for micro air vehicles. Phil. Trans. R. Soc. A 360, 273–290.Google Scholar