Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T15:06:20.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduced-order modelling of radiative transfer effects on Rayleigh–Bénard convection in a cubic cell

Published online by Cambridge University Press:  24 June 2020

Laurent Soucasse Open the ORCID record for Laurent Soucasse [Opens in a new window] ,
Bérengère Podvin Open the ORCID record for Bérengère Podvin [Opens in a new window] ,
Philippe Rivière  and
Anouar Soufiani
Laurent Soucasse*
Affiliation:
Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 8-10 rue Joliot Curie,91192 Gif-sur-Yvette, France
Bérengère Podvin
Affiliation:
LIMSI, CNRS, Université Paris-Saclay, Bât 507, rue du Belvédère, Campus Universitaire,91405 Orsay, France
Philippe Rivière
Affiliation:
Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 8-10 rue Joliot Curie,91192 Gif-sur-Yvette, France
Anouar Soufiani
Affiliation:
Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 8-10 rue Joliot Curie,91192 Gif-sur-Yvette, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

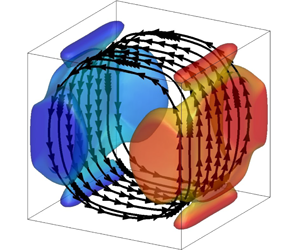
This paper presents a reduced-order modelling strategy for Rayleigh–Bénard convection of a radiating gas, based on the proper orthogonal decomposition (POD). Direct numerical simulation (DNS) of coupled natural convection and radiative transfer in a cubic Rayleigh–Bénard cell is performed for an $\text{air}/\text{H}_{2}\text{O}/\text{CO}_{2}$ mixture at room temperature and at a Rayleigh number of $10^{7}$. It is shown that radiative transfer between the isothermal walls and the gas triggers a convection growth outside the boundary layers. Mean and turbulent kinetic energy increase with radiation, as well as temperature fluctuations to a lesser extent. As in the uncoupled case, the large-scale circulation (LSC) settles in one of the two diagonal planes of the cube with a clockwise or anticlockwise motion, and experiences occasional brief reorientations which are rotations of $\unicode[STIX]{x03C0}/2$ of the LSC in the horizontal plane. A POD analysis is conducted and reveals that the dominant POD eigenfunctions are preserved with radiation while POD eigenvalues are increased. Two POD-based reduced-order models including radiative transfer effects are then derived: the first one is based on coupled DNS data while the second one is an a priori model based on uncoupled DNS data. Owing to the weak temperature differences, radiation effects on mode amplitudes are linear in the models. Both models capture the increase in energy with radiation and are able to reproduce the low-frequency dynamics of reorientations and the high-frequency dynamics associated with the LSC velocity observed in the coupled DNS.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 898 , 10 September 2020 , A2
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bai, K., Ji, D. & Brown, E. 2016 Ability of a low-dimensional model to predict geometry-dependent dynamics of large-scale coherent structures in turbulence. Phys. Rev. E 93, 023117.Google ScholarPubMed
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
Bdéoui, F. & Soufiani, A. 1997 The onset of Rayleigh–Bénard instability in molecular radiating gases. Phys. Fluids 9, 3858–3872.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Borget, V., Bdéoui, F., Soufiani, A. & Le Quéré, P. 2001 The transverse instability in a differentially heated vertical cavity filled with molecular radiating gases. I. Linear stability analysis. Phys. Fluids 13 (5), 1492–1507.CrossRefGoogle Scholar
Bouillaut, V., Lepot, S., Aumaître, S. & Gallet, B. 2019 Transition to the ultimate regime in a radiatively driven convection experiment. J. Fluid Mech. 861, R5.CrossRefGoogle Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
Czarnota, T. & Wagner, C. 2016 Turbulent convection and thermal radiation in a cuboidal Rayleigh–Bénard cell with conductive plates. Intl J. Heat Fluid Flow 57, 150–172.CrossRefGoogle Scholar
Foroozani, N., Niemela, J. J., Armenio, V. & Sreenivasan, K. R. 2017 Reorientations of the large-scale flow in turbulent convection in a cube. Phys. Rev. E 95, 033107.Google Scholar
Gille, J. & Goody, R. 1964 Convection in a radiating gas. J. Fluid Mech. 20, 47–79.CrossRefGoogle Scholar
Goody, R. M. 1956 The influence of radiative transfer on cellular convection. J. Fluid Mech. 1, 424–435.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Holmes, P., Lumley, J. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
Hutchinson, J. E. & Richards, R. F. 1999 Effect of nongray gas radiation on thermal stability in carbon dioxied. J. Thermophys. Heat Transfer 13, 25–32.CrossRefGoogle Scholar
Kogawa, T., Okajima, J., Sakurai, A., Komiya, A. & Maruyama, S. 2017 Influence of radiation effect on turbulent natural convection in cubic cavity at normal temperature atmospheric gas. Intl J. Heat Mass Transfer 104, 456–466.CrossRefGoogle Scholar
Lan, C. H., Ezekoye, O. A., Howell, J. R. & Ball, K. S. 2003 Stability analysis for three-dimensional Rayleigh–Bénard convection with radiatively participating medium using spectral methods. Intl J. Heat Mass Transfer 46, 1371–1383.CrossRefGoogle Scholar
Lepot, S., Aumaître, S. & Gallet, B. 2018 Radiative heating achieves the ultimate regime of thermal convection. Proc. Natl Acad. Sci. USA 115 (36), 8937–8941.CrossRefGoogle ScholarPubMed
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42 (1), 335–364.CrossRefGoogle Scholar
Lumley, J. L. & Podvin, B. 1996 Dynamical systems theory and extra rates of strain in turbulent flows. J. Exp. Therm. Fluid Sci. 267, 1–10.Google Scholar
Mishra, P. K., De, A. K., Verma, M. K. & Eswaran, V. 2011 Dynamics of reorientations and reversals of large-scale flow in Rayleigh–Bénard convection. J. Fluid Mech. 668, 480–499.CrossRefGoogle Scholar
Mishra, S. C., Akhtar, A. & Garg, A. 2014 Numerical analysis of Rayleigh–Bénard convection with and without volumetric radiation. Numer. Heat Transfer A 65 (2), 144–164.CrossRefGoogle Scholar
Park, H. M., Sung, M. C. & Chung, J. S. 2004 Stabilization of Rayleigh–Bénard convection by means of mode reduction. Proc. R. Soc. Lond. A 460, 1807–1830.CrossRefGoogle Scholar
Pierrot, L., Rivière, P., Soufiani, A. & Taine, J. 1999 A fictitious-gas-based absorption distribution function global model for radiative transfer in hot gases. J. Quant. Spectrosc. Radiat. Transfer 62, 609–624.CrossRefGoogle Scholar
Podvin, B. & Le Quéré, P. 2001 Low-order models for the flow in a differentially heated cavity. Phys. Fluids 13 (11), 3204–3214.CrossRefGoogle Scholar
Podvin, B. & Sergent, A. 2015 A large-scale investigation of wind reversal in a square Rayleigh–Bénard cell. J. Fluid Mech. 766, 172–201.CrossRefGoogle Scholar
Podvin, B. & Sergent, A. 2017 Precursor for wind reversal in a square Rayleigh–Bénard cell. Phys. Rev. E 95, 013112.Google Scholar
van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2015 Plume emission statistics in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 772, 5–15.CrossRefGoogle Scholar
Prasanna, S. & Venkateshan, S. P. 2014 Convection induced by radiative cooling of a layer of participating medium. Phys. Fluids 26 (5), 056603.CrossRefGoogle Scholar
Puigjaner, D., Herrero, J., Simo, C. & Giralt, F. 2008 Bifurcation analysis of steady Rayleigh–Bénard convection in a cubical cavity with conducting sidewalls. J. Fluid Mech. 598, 393–427.CrossRefGoogle Scholar
Sakurai, A., Matsubara, K., Takakuwa, K. & Kanbayashi, R. 2012 Radiation effects on mixed turbulent natural and forced convection in a horizontal channel using direct numerical simulation. Intl J. Heat Mass Transfer 55, 2539–2548.CrossRefGoogle Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamic of coherent structures. Part I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Soucasse, L.2013 Effets des transferts radiatifs sur les écoulements de convection naturelle dans une cavité différentiellement chauffée en régimes transitionnel et faiblement turbulent. PhD thesis, École Centrale Paris, France.Google Scholar
Soucasse, L., Podvin, B., Rivière, P. & Soufiani, A. 2019 Proper orthogonal decomposition analysis and modelling of large-scale flow reorientations in a cubic Rayleigh–Bénard cell. J. Fluid Mech. 881, 23–50.CrossRefGoogle Scholar
Soucasse, L., Rivière, P. & Soufiani, A. 2014a Effects of molecular gas radiation on Rayleigh–Bénard convection in a 3D cubical cavity. In Proceedings of the 15th International Heat Transfer Conference, pp. IHTC15–9563. Begell House.Google Scholar
Soucasse, L., Rivière, P. & Soufiani, A. 2016 Natural convection in a differentially heated cubical cavity under the effects of wall and molecular gas radiation at Rayleigh numbers up to 3 × 109. Intl J. Heat Fluid Flow 61‐B, 510–530.CrossRefGoogle Scholar
Soucasse, L., Rivière, P., Soufiani, A., Xin, S. & Le Quéré, P. 2014b Transitional regimes of natural convection in a differentially heated cavity under the effects of wall and molecular gas radiation. Phys. Fluids 26, 024105.CrossRefGoogle Scholar
Soucasse, L., Rivière, P., Xin, S., Le Quéré, P. & Soufiani, A. 2012 Numerical study of coupled molecular gas radiation and natural convection in a differentially heated cubical cavity. Comput. Thermal Sci. 4, 335–350.CrossRefGoogle Scholar
Soufiani, A. 1991 Temperature turbulence spectrum for high-temperature radiating gases. J. Thermophys. 5 (4), 489–494.CrossRefGoogle Scholar
Spiegel, E. A. 1960 The convective instability of a radiating fluid layer. Astrophys. J. 132, 716–728.CrossRefGoogle Scholar
Vasiliev, A., Frick, P., Kumar, A., Stepanov, R., Sukhanovskii, A. & Verma, M. K. 2019 Transient flows and reorientations of large-scale convection in a cubic cell. Intl Commun. Heat Mass Transfer 108, 104319.CrossRefGoogle Scholar
Verdoold, J., Tummers, M. J. & Hanjalić, K. 2009 Prime modes of fluid circulation in large-aspect-ratio turbulent Rayleigh–Bénard convection. Phys. Rev. E 80, 037301.Google ScholarPubMed
Xin, S., Chergui, J. & Le Quéré, P. 2008 3D spectral parallel multi-domain computing for natural convection flows. In Parallel Computational Fluid Dynamics, pp. 163–171. Springer.Google Scholar
Xin, S. & Le Quéré, P. 2002 An extended Chebyshev pseudo-spectral benchmark for the 8 : 1 differentially heated cavity. Intl J. Heat Mass Transfer 40, 981–998.Google Scholar