Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-06T11:07:14.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursive dynamic mode decomposition of transient and post-transient wake flows

Published online by Cambridge University Press:  21 November 2016

Bernd R. Noack Open the ORCID record for Bernd R. Noack [Opens in a new window] ,
Witold Stankiewicz ,
Marek Morzyński  and
Peter J. Schmid
Bernd R. Noack*
Affiliation:
Laboratoire d’Informatique pour la Mécanique et les Sciences de l’Ingénieur, LIMSI-CNRS, Rue John von Neumann, Campus Universitaire d’Orsay, Bât 508, F-91403 Orsay, France Institut für Strömungsmechanik, Technische Universität Berlin, Hermann-Blenk-Straße 37, D-38108 Braunschweig, Germany
Witold Stankiewicz
Affiliation:
Chair of Virtual Engineering, Poznań University of Technology, ul. Jana Pawła II 24, 60-965 Poznań, Poland
Marek Morzyński
Affiliation:
Chair of Virtual Engineering, Poznań University of Technology, ul. Jana Pawła II 24, 60-965 Poznań, Poland
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

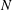A novel data-driven modal decomposition of fluid flow is proposed, comprising key features of proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD). The first mode is the normalized real or imaginary part of the DMD mode that minimizes the time-averaged residual. The $N$th mode is defined recursively in an analogous manner based on the residual of an expansion using the first 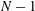$N-1$ modes. The resulting recursive DMD (RDMD) modes are orthogonal by construction, retain pure frequency content and aim at low residual. Recursive DMD is applied to transient cylinder wake data and is benchmarked against POD and optimized DMD (Chen et al., J. Nonlinear Sci., vol. 22, 2012, pp. 887–915) for the same snapshot sequence. Unlike POD modes, RDMD structures are shown to have purer frequency content while retaining a residual of comparable order to POD. In contrast to DMD, with exponentially growing or decaying oscillatory amplitudes, RDMD clearly identifies initial, maximum and final fluctuation levels. Intriguingly, RDMD outperforms both POD and DMD in the limit-cycle resolution from the same snapshots. Robustness of these observations is demonstrated for other parameters of the cylinder wake and for a more complex wake behind three rotating cylinders. Recursive DMD is proposed as an attractive alternative to POD and DMD for empirical Galerkin models, in particular for nonlinear transient dynamics.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 843 - 872
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagheri, S. 2013 Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596–623.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Bergmann, M. & Cordier, L. 2008 Optimal control of the cylinder wake in the laminar regime by trust-region methods and POD reduced order models. J. Comput. Phys. 227, 7813–7840.Google Scholar
Bourgeois, J. A., Martinuzzi, R. J. & Noack, B. R. 2013 Generalised phase average with applications to sensor-based flow estimation of the wall-mounted square cylinder wake. J. Fluid Mech. 736, 316–350.Google Scholar
Brunton, S. L. & Noack, B. R. 2015 Closed-loop turbulence control: progress and challenges. Appl. Mech. Rev. 67 (5), 050801.CrossRefGoogle Scholar
Chen, K. K., Tu, J. H. & Rowley, C. W. 2012 Variants of dynamic mode decomposition: boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 22 (6), 887–915.CrossRefGoogle Scholar
Coats, C. M. 1997 Coherent structures in combustion. Prog. Energy Combust. Sci. 22, 427–509.CrossRefGoogle Scholar
Courant, R. & Hilbert, D. 1989 Methods of Mathematical Physics, vol. 1. Wiley-VCH.Google Scholar
Deane, A. E., Kevrekidis, I. G., Karniadakis, G. E. & Orszag, S. A. 1991 Low-dimensional models for complex geometry flows: application to grooved channels and circular cylinders. Phys. Fluids A 3, 2337–2354.Google Scholar
Fletcher, C. A. J. 1984 Computational Galerkin Methods, 1st edn. Springer.Google Scholar
Föppl, L. 1913 Wirbelbewegung hinter einen Kreiszylinder (transl.: vortex motion behind a circular cylinder). Sitzb. d. k. bayr. Akad. d. Wiss. 1, 1–18.Google Scholar
Galerkin, B. G. 1915 Rods and plates: series occurring in various questions regarding the elastic equilibrium of rods and plates (translated). Vestn. Inzhen. 19, 897–908.Google Scholar
Gerhard, J., Pastoor, M., King, R., Noack, B. R., Dillmann, A., Morzyński, M. & Tadmor, G. 2003 Model-based control of vortex shedding using low-dimensional Galerkin models. In 33rd AIAA Fluids Conference and Exhibit, Orlando, Florida, USA, Paper 2003-4262.Google Scholar
Han, Z.-H., Stefan, G. & Zimmermann, R. 2013 Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 25 (1), 177–189.Google Scholar
Hoarau, C., Borée, J., Laumonier, J. & Gervais, Y. 2006 Analysis of the wall pressure trace downstream of a separated region using extended proper orthogonal decomposition. Phys. Fluids 18, 055107.Google Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1998 Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 1st edn. Cambridge University Press.Google Scholar
Jørgensen, B. H., Sørensen, J. N. & Brøns, M. 2003 Low-dimensional modeling of a driven cavity flow with two free parameters. Theor. Comput. Fluid Dyn. 16, 299–317.Google Scholar
von Kármán, T. & Rubach, H. 1912 Über den Mechanismus des Flüssigkeits- und Luftwiderstandes. Phys. Zeitschr. XIII, 49–59.Google Scholar
Lorenz, E. N. 1956 Empirical orthogonal functions and statistical weather prediction. Tech. Rep.. MIT, Department of Meteorology, Statistical Forecasting Project.Google Scholar
Lorenz, E. N. 1963 Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141.2.0.CO;2>CrossRefGoogle Scholar
Lugt, H. J. 1995 Vortex Flow in Nature and Technology. Krieger Publishing Company.Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Wave Propagation (ed. Yaglom, A. M. & Tatarski, V. I.), pp. 166–178.Google Scholar
Mezić, I. 2013 Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 367–378.CrossRefGoogle Scholar
Noack, B. R. 2016 From snapshots to modal expansions – bridging low residuals and pure frequencies. J. Fluid Mech. 802, 1–4.Google Scholar
Noack, B. R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
Noack, B. R., Pelivan, I., Tadmor, G., Morzyński, M. & Comte, P. 2004 Robust low-dimensional Galerkin models of natural and actuated flows. In Fourth Aeroacoustics Workshop, pp. 0001–0012. RWTH Aachen.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.CrossRefGoogle Scholar
Orszag, S. A. 1971 Numerical simulation of incompressible flows within simple boundaries: accuracy. J. Fluid Mech. 49, 75–112.Google Scholar
Rom-Kedar, V., Leonard, A. & Wiggins, S. 1990 An analytical study of transport, mixing and chaos in unsteady vortical flow. J. Fluid Mech. 214, 347–394.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 645, 115–127.CrossRefGoogle Scholar
Schlegel, M., Noack, B. R., Jordan, P., Dillmann, A., Gröschel, E., Schröder, W., Wei, M., Freund, J. B., Lehmann, O. & Tadmor, G. 2012 On least-order flow representations for aerodynamics and aeroacoustics. J. Fluid Mech. 697, 367–398.CrossRefGoogle Scholar
Schmid, P. J. 2010 Dynamic mode decomposition for numerical and experimental data. J. Fluid. Mech 656, 5–28.CrossRefGoogle Scholar
Schumm, M., Berger, E. & Monkewitz, P. A. 1994 Self-excited oscillations in the wake of two-dimensional bluff bodies and their control. J. Fluid Mech. 271, 17–53.Google Scholar
Sieber, M., Paschereit, C. O. & Oberleithner, K. 2016 Spectral proper orthogonal decomposition. J. Fluid Mech. 792, 798–828.CrossRefGoogle Scholar
Siegel, S. G., Seidel, J., Fagley, C., Luchtenburg, D. M., Cohen, K. & Mclaughlin, T. 2008 Low dimensional modelling of a transient cylinder wake using double proper orthogonal decomposition. J. Fluid Mech. 610, 1–42.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Maths XLV, 561–571.Google Scholar
Suh, Y. K. 1993 Periodic motion of a point vortex in a corner subject to a potential flow. J. Phys. Soc. Japan 62, 3441–3445.CrossRefGoogle Scholar
Taylor, C. & Hood, P 1973 A numerical solution of the Navier–Stokes equations using the finite element technique. Comput. Fluids 1 (1), 73–100.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Zebib, A. 1987 Stability of viscous flow past a circular cylinder. J. Engng Maths 21, 155–165.Google Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–795.Google Scholar